Simplifying Improper Fractions Worksheets
About These 15 Worksheets
An improper fraction is one where the numerator (top number) is larger than or equal to the denominator (bottom number). For example, 7/4 or 9/3 are improper fractions. Unlike mixed numbers, which combine a whole number with a fraction (like 1 3/4), improper fractions don’t separate out the whole number.
These worksheets are used by teachers, tutors, and educators to provide practice and reinforcement for students in the process of converting these fractions into their simplest or most familiar forms. Before diving into the specifics of the worksheets, it’s essential to understand what an improper fraction is and how it relates to other types of fractions.
Types of Exercises on the Worksheets
Identification Exercises – These exercises help students identify and differentiate between proper fractions, improper fractions, and mixed numbers. Students recognize the structure of various types of fractions.
Example: Which of the following is an improper fraction? 3/2, 1 1/3, 5/7.
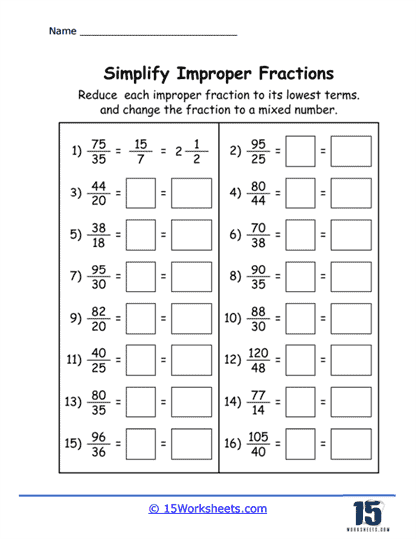
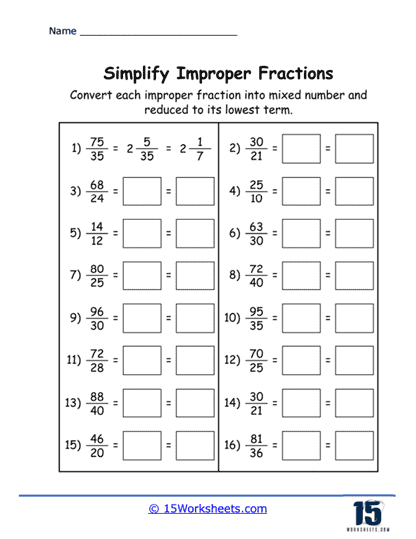
Conversion to Mixed Numbers – To convert improper fractions into mixed numbers. Students learn to separate out the whole number from the fractional part, thus understanding the relationship between improper fractions and mixed numbers.
Example: Convert 11/3 into a mixed number; such as 3 2/3.
Conversion to Improper Fractions – To convert mixed numbers into improper fractions. This reinforces the concept of mixed numbers as combinations of whole numbers and fractions.
Example: Convert 2 2/5 into an improper fraction; such as 12/5.
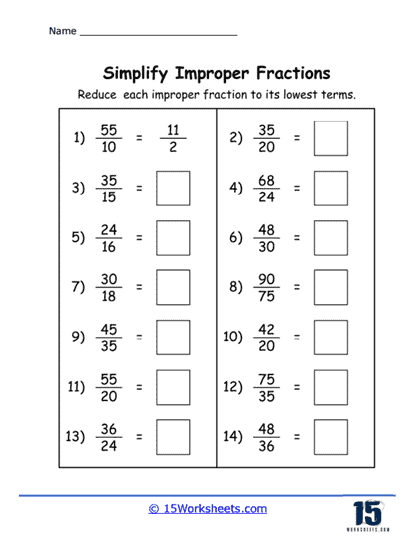
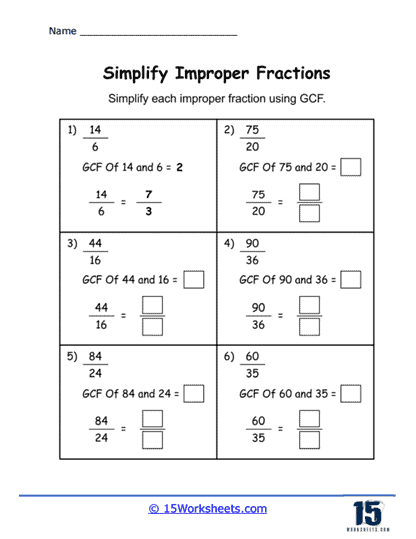
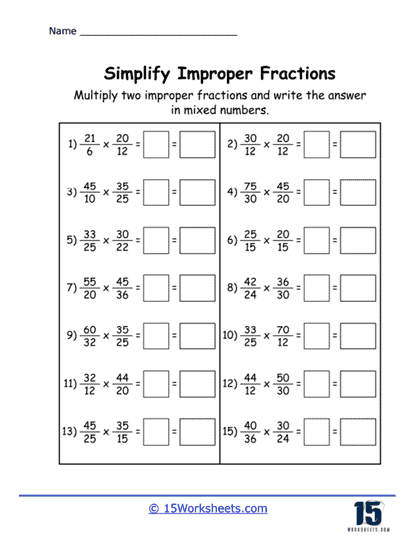
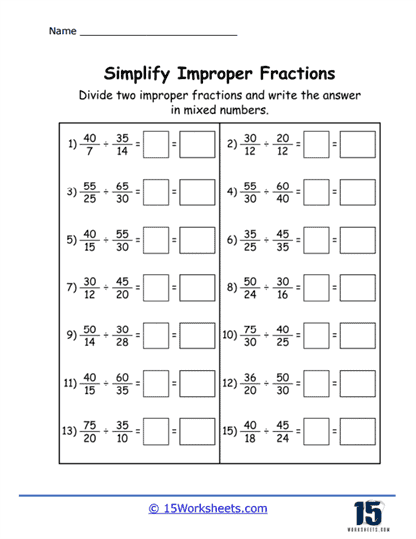
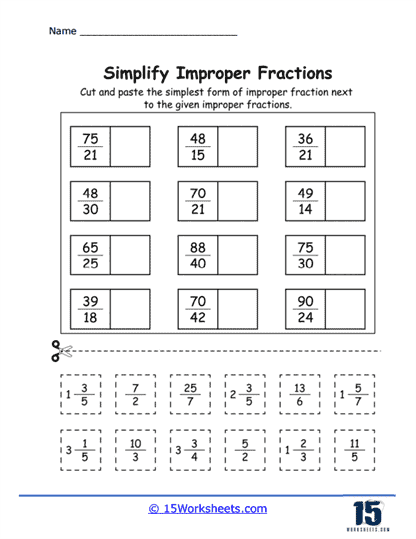
Simplification of Fractions – Students practice reducing fractions to their simplest form by identifying and canceling out common factors in the numerator and denominator. By repeatedly engaging in the process, students internalize the idea of simplest form and become proficient in factorization and simplification.
Example: Simplify the fraction 6/8.
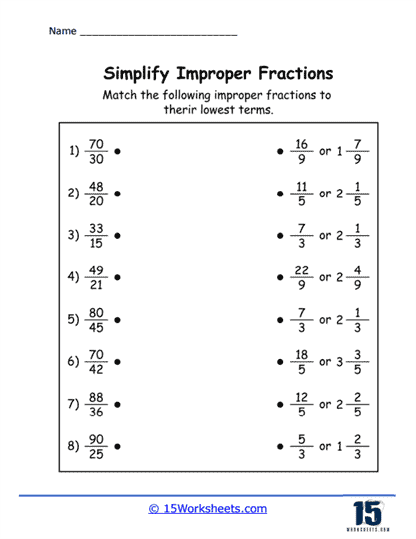
Comparing and Ordering Improper Fractions – Students learn to determine the relative size of different improper fractions. This helps students understand the value of fractions, which is crucial when adding, subtracting, or using them in other mathematical operations.
Example: Arrange the following fractions in ascending order: 5/2, 7/3, 9/4.
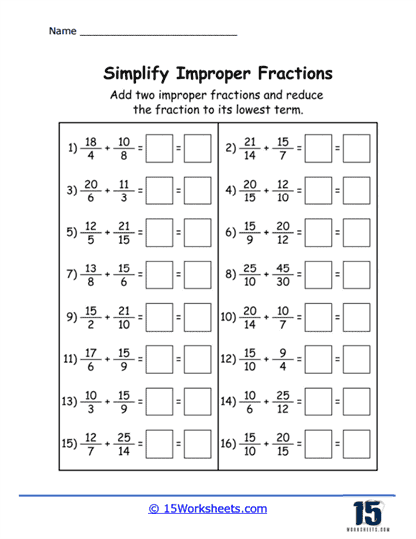
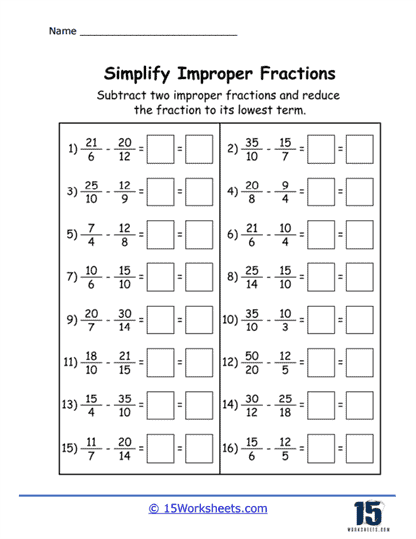
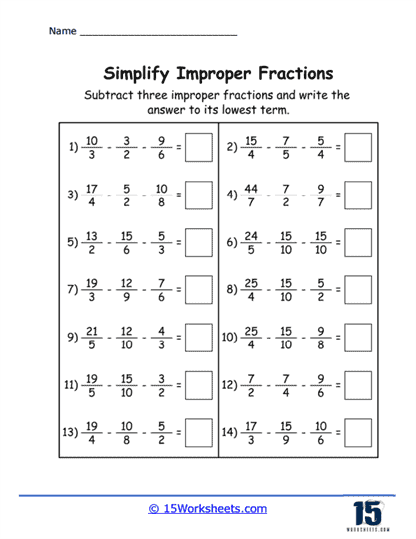
Addition and Subtraction with Improper Fractions – Students learn to add or subtract improper fractions, often converting between mixed numbers and improper fractions in the process. Mastery of basic arithmetic operations with improper fractions.
Example: Add 7/4 and 5/3.
Steps to Simplifying Improper Fractions
Simplifying improper fractions often involves converting them into mixed numbers. A mixed number consists of a whole number and a proper fraction combined. Here’s how to simplify improper fractions:
Step #1 – Divide the numerator by the denominator. This will give you a whole number (the quotient) and possibly a remainder.
Step #2 – Write down the whole number. This is the number of times the denominator fits into the numerator.
Step #3 – Place the remainder over the original denominator. This becomes the fractional part of the mixed number.
Step #4 – Combine the whole number and the new fraction to get a mixed number.
Example 1: Simplify 7/4
Step #1 – Divide 7 by 4. Quotient = 1, Remainder = 3.
Step #2 – The whole number is 1.
Step #3 – The fraction is 3/4.
Step #4 – Combine them: 7/4 = 1 3/4
Example 2: Simplify 11/3
Step #1 – Divide 11 by 3. Quotient = 3, Remainder = 2.
Step #2 – The whole number is 3.
Step #3 – The fraction is 2/3.
Step #4 – Combine them: 11/3 = 3 2/3