Decomposing Fractions Worksheets

All About These 15 Worksheets

This series of 15 worksheets on Decomposing Fractions is designed to help students master this fundamental math skill. Decomposing fractions involves breaking a fraction down into smaller parts, which can be useful in solving more complex problems involving fractions.

Each worksheet in the series includes a variety of problems with varying levels of difficulty. The problems require students to decompose fractions into smaller fractions or to combine fractions to form larger ones.

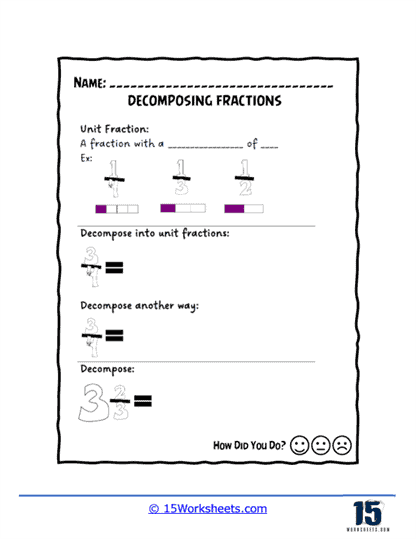
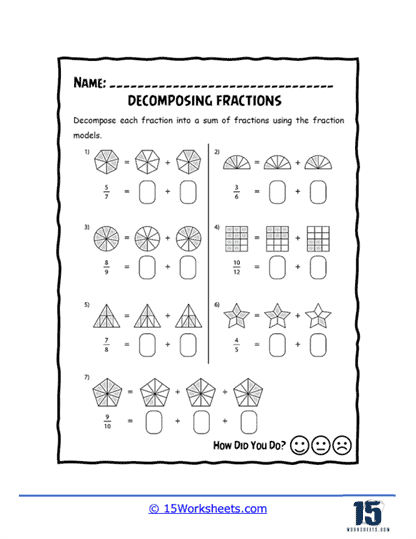
First up: “Fraction Bars,” “Decomposing Box Fractions,” and the heartbreakingly adorable “Decomposing Heart Fractions.” These worksheets are like math’s version of finger painting—visual, hands-on, and just the right amount of messy. Kids get to physically see how fractions break down, whether it’s through neatly stacked bars, suspiciously cube-shaped boxes, or a Valentine’s Day massacre of numerators. If Picasso had a protractor, he’d approve.

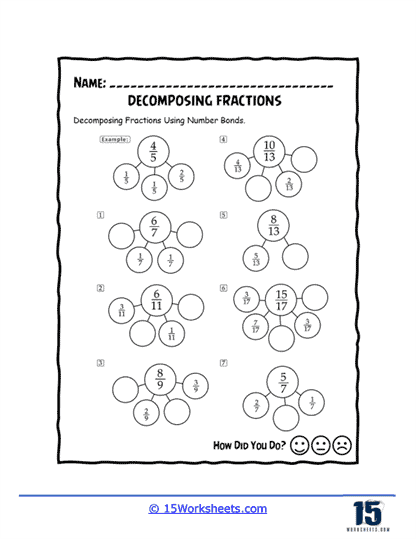
Next, we bring out the nerdy matchmakers: “Using Number Bonds,” “Fraction Number Bonds,” and “Decomposing Unit Fractions.” These are the worksheets where fractions pair off, mingle, and form beautiful little numerical relationships. Think speed dating for denominators. Students learn how to take a chunk of something (like 3/4) and split it into neat little pieces, like (1/4 + 1/4 + 1/4), which is essentially what happens when you try to share a single cookie with two very judgmental siblings.

Enter “Pick Apart Fractions” and “Fraction Expressions.” These sheets turn fractions into full-blown chatterboxes. Instead of simply being fractions, now they want to talk about themselves. “Hi, I’m 2/3, but you can also call me 1/3 + 1/3 or maybe 4/6 if you’re nasty.” Students write out equivalent expressions, break them down in words, and start to see just how many alter egos a single fraction can have. Basically, fractions are the shape-shifters of the math world.

Then we have the big-brain section: “Decompose Fractions Many Ways,” “Crumble the Fraction,” and “Breaking Down Fractions.” These worksheets demand flexibility, creativity, and just a dash of chaos. Here, students are asked to decompose the same fraction in multiple ways-because apparently, fractions are like onions and ogres: they have layers. These activities challenge kids to say, “Yes, I can write 4/5 as 1/5 + 1/5 + 2/5 AND still have time for lunch.” It’s beautiful, chaotic math philosophy.

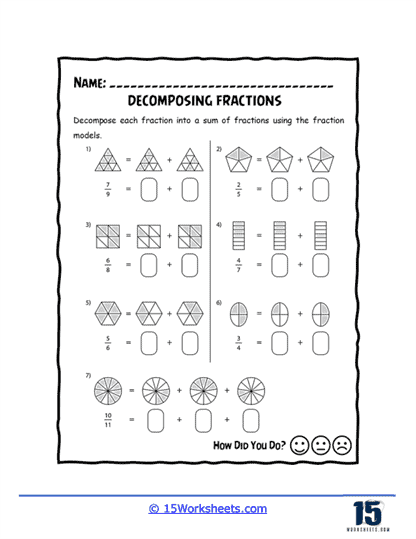
We end with the high society of fraction decomposition: “Fraction Models,” “Decomposing Fraction Models,” and “Decomposing Mixed Numbers.” These are for students who are ready to level up and break apart not just fractions, but mixed numbers-those sneaky devils that act like they’re whole but secretly still part fraction. With models and visual aids, students learn how to deconstruct these bougie math terms like pros. It’s basically Marie Kondo meets math: does this part of your number spark joy? No? Break it down.

These worksheets are designed to be both engaging and informative, with detailed instructions, visual aids, and math puzzles. They also provide ample space for students to show their work and write down their answers, allowing them to develop their problem-solving skills through self-review or feedback given by their teachers or peers.

This series is most suitable for students in grades 5 to 8. It can be used in the classroom as a supplement to the math curriculum or at home as a way for parents to help their children practice and reinforce their math skills.

How Do You Decompose Fractions?

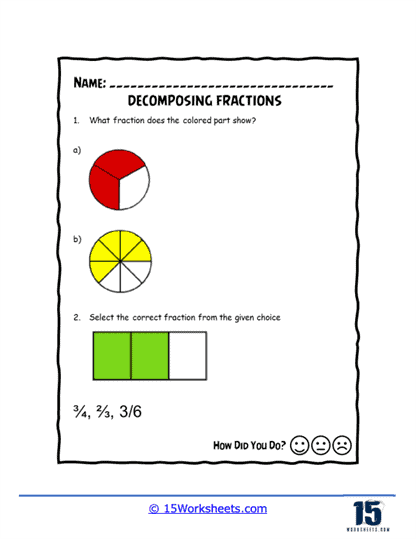
Decomposing fractions means breaking a fraction into the sum of smaller fractions with the same denominator. It can be a useful way to simplify problems, make sense of fractions, or teach fraction concepts. Here’s a step-by-step guide that teachers can share with their students to help them in decomposing fractions:

Choose Smaller Fractions with the Same Denominator – Identify fractions with the same denominator that, when added together, will equal the original fraction. There can be more than one correct answer when decomposing a fraction, as it can be broken down into different combinations of smaller fractions.

For example, let’s say you want to decompose the fraction 5/6. Here are two possible ways to decompose it:

Option 1:

• 1/6 + 1/6 + 1/6 + 1/6 + 1/6
• 5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6

Option 2:

• 1/6 + 4/6
• 5/6 = 1/6 + 4/6 (Note that 4/6 can be further simplified to 2/3)

Write the Decomposition – Write the original fraction as the sum of the smaller fractions you have chosen. You can write it in equation form, as shown in the examples above.

Simplify if Necessary – If any of the smaller fractions in your decomposition can be simplified further, do so. For example, in Option 2 above, we can simplify the decomposition as follows:

5/6 = 1/6 + 2/3

Decomposing fractions can also be done using mixed numbers or improper fractions. The key is to break down the original fraction into a sum of smaller fractions with the same denominator, which can help you better understand or manipulate the fractions in various mathematical or real-world situations.

Real World Applications

Decomposing fractions plays a valuable role in making everyday tasks more approachable and efficient. By breaking down fractions into smaller, more manageable parts, we can gain clearer insights into the quantities involved in our daily decisions. This practice isn’t just a mathematical exercise-it’s a powerful tool that supports clarity, precision, and problem-solving across diverse real-world scenarios.

Consider common activities such as cooking, budgeting, and time management. When preparing a meal and adjusting a recipe to serve fewer people, decomposing fractions allows for accurate measurement of ingredients, ensuring consistent results. Similarly, when planning a budget or distributing shared expenses, breaking fractions down helps clarify how resources are being allocated, making financial decisions more transparent and less overwhelming. Even in organizing a busy schedule, fractional thinking can help divide time effectively, helping you balance responsibilities while identifying where time can be gained or lost.

Beyond practical life management, decomposing fractions is also critical in fields that depend on precision and understanding of proportions-like education, construction, or even the arts. Teachers often use decomposition to help students grasp how fractions work and relate to each other. Designers and builders rely on it for accurate scaling and material division. In artistic endeavors such as sewing or woodworking, decomposing fractional measurements ensures symmetry and detail in the final product. Whether you’re analyzing a basketball player’s shooting percentage or preparing canvas sizes for a painting, the ability to see and work with parts of a whole can make all the difference.