Converting Fractions Worksheets
About These 15 Worksheets
These worksheets are filled with exercises that help you to understand and master the concept of changing fractions (which represent a part of a whole) into decimals (based on ‘tenths’) or percentages (part of a hundred). To appreciate the value of these worksheets, you need to understand what fractions, decimals, and percentages are, and how they’re related.
A fraction is a way of expressing a quantity by using two whole numbers, with one on top (the numerator) and one at the bottom (the denominator). It represents a part of a whole. For example, if you have 1 apple out of 4, you can represent this as the fraction 1/4.
A decimal represents a part of a whole number and is based on the base 10 numbering system. For example, the decimal 0.5 represents half of a whole or 1/2.
A percentage represents a number out of 100. So, 50% means 50 out of 100 or half.
These three ways of representing numbers are interconnected. For example, the fraction 1/2, the decimal 0.5, and the percentage 50% all represent the same thing.
Types of Problems on These Worksheets
1. Visual Conversions & Colorful Insights
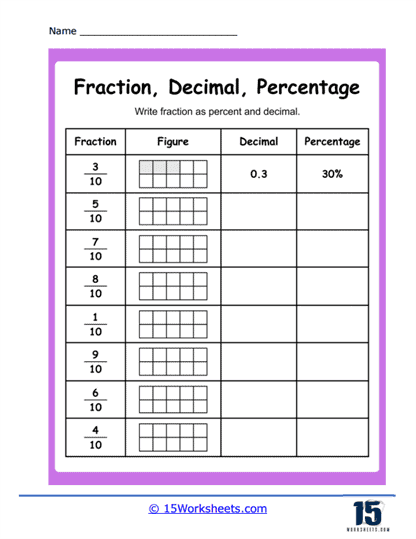
We begin with the artistry of numbers. “Color Tenths as Decimals and Percents,” “Colored Percentages,” and “Shade the Grid“ bring students face‑to‑face with the colorful soul of fractions. Imagine tiny ten‑piece pizzas: students color two out of ten, label it 0.2, then slap on that shiny 20%. It’s a feast of hues and numbers! Shade the Grid adds a splash of spatial reasoning-coloring blocks reinforces how decimals and fractions map onto actual space. By the time they finish, students can practically paint their way from halves to percentages (and yes-art class is secretly happening here).
2. Direct Conversions & Number Fluency
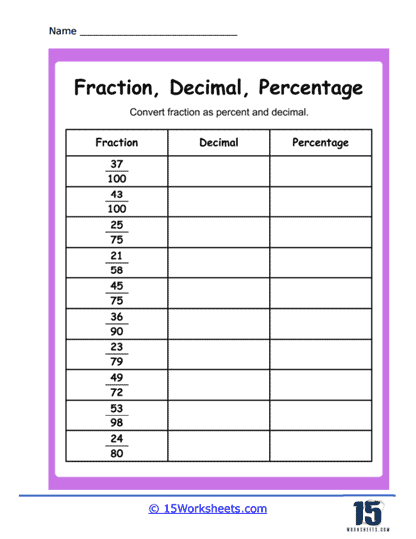
This is the meat and potatoes of converting fractions. “Fraction to Percentage,” “Fractions to Percent and Decimals,” “Fractions to Percents,” “Convert to Hundredths,” and “Digging Decimals“ demand that students switch back and forth between fraction, decimal, and percent with the agility of a ninja. Want to turn 3/4 into 75% or into 0.75? No problem. Thanks to the whirlwind of exercises, kids start speaking in math‑tri‑lingual-fraction, decimal, percent-without even blinking. Digging Decimals unearths those hidden decimals in everyday contexts. By the end, kids don’t just convert-they teleport, warp, and morph numbers at will.
3. Matching, Charts & Missing Links
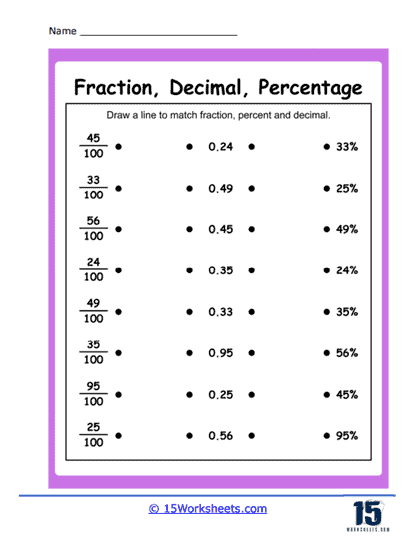
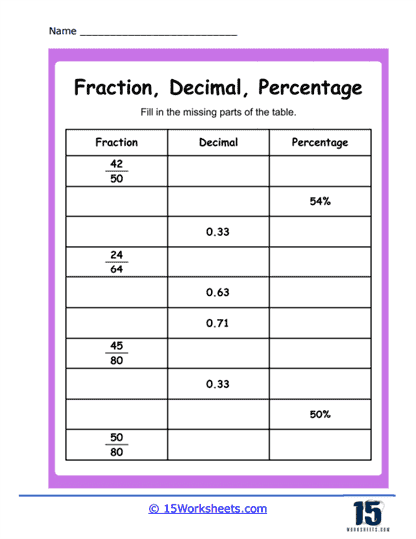
Here things get playful with detective vibes. “Matching Fraction Conversions,” “Fraction Conversion Chart,” “Missing Values,” and “Connect Conversions“ turn conversion into an interactive puzzle hunt. A fraction chart becomes their treasure map. They pair ⅖ with 0.4, hunt for missing numbers, and draw lines to link equivalents. It’s fractions meets matching socks-finding the perfect partner. Students flex their pattern‑recognition muscles and logical thinking. Plus, they get to revel in that small thrill when they spot that all three forms are the same number in disguise.
4. Multiple Choice & Quiz‑Style Recall
Mental recall gets its moment in “Multiple Choice“. These carefully curated snippets test whether students have internalized conversion rules or are just relying on coloring fun. It’s the moment of truth-no pens, no grids-just fractions, decimals, percents, and multiple‑choice options. Quick reactions, sharpened instincts. It’s also excellent training for standardized‑test showdowns-and a taste of math adrenaline.
5. Themed Drills & Quirky Fraction Sets
“Convert Fractions of 5s“ brings system‑specific drills: how do you convert 1/5, 2/5, 3/5, and so on into decimals and percents? It’s thematic training for the five tribes of fractions-each with a motto (“We’re always .2, 40%, 60%, 80%, or 100%!”). Like learning the chorus of a catchy song, pattern drills build lasting memory. Kids emerge humming fraction‑songs, happily surprised at how memorably consistent 5ths are. (One might even start tapping their pencil to 0.2, 0.4 beats…)
The Math Skills They Work On
Builds Fundamental Skills – These worksheets help to reinforce the understanding that fractions, decimals, and percentages are just different ways of expressing the same thing. This understanding is foundational for many topics in math, including algebra, statistics, and calculus.
Improves Number Sense – By regularly converting between fractions, decimals, and percentages, you’ll develop a better feel for numbers and their relationships, an essential aspect of number sense.
Enhances Problem-Solving Abilities – Conversion exercises often involve problem-solving and reasoning skills, such as when dealing with word problems or multiple-step problems.
Facilitates Learning of Future Topics – The ability to comfortably convert between fractions, decimals, and percentages will aid in learning more complex concepts, such as ratios, proportions, and rates.
When Will You Use This Skill in Real Life?
Money – When dealing with money, understanding decimals is essential. For example, $0.75 is the decimal equivalent of the fraction 3/4 of a dollar.
Shopping – Percentages are often used in discounts and sales. For example, if an item is 25% off, that’s the same as 1/4 off the original price.
Cooking – Recipes often involve fractions. Being able to convert these fractions to decimals can be helpful when using measuring tools that are marked in decimals.
Statistics – Data is often presented in percentages in news reports, research findings, or when understanding grades at school.
How Do You Convert a Fraction to a Decimal?
Step 1) Understand the Principle
The denominator of a fraction tells you the number of equal parts that a whole is divided into, while the numerator tells you how many of those parts you have. So, when you’re converting a fraction to a decimal, what you’re really doing is figuring out what part of a whole number (expressed in the base 10 system) your fraction represents.
Step 2) Identify the Type of Fraction
It’s important to identify if your fraction is a simple fraction or a complex fraction. A simple fraction has a denominator that’s a power of 10 (10, 100, 1000, etc.), which makes it easier to convert into a decimal. A complex fraction has a denominator that isn’t a power of 10.
Step 3) Conversion
Simple Fractions – For fractions where the denominator is a power of 10, simply write down the numerator in the place value that corresponds to the denominator. For example, for the fraction 7/10, the decimal is 0.7. For 7/100, it’s 0.07.
Complex Fractions – For fractions where the denominator isn’t a power of 10, you can convert them to decimals by using division. Here, the numerator is the dividend (what you’re dividing) and the denominator is the divisor (what you’re dividing by). For example, to convert 3/4 to a decimal, you divide 3 by 4, which equals 0.75.
Step 4) Long Division (if necessary)
If the division isn’t simple to do in your head, you can use long division. For example, to convert 2/3 to a decimal:
Divide 2 by 3. Because 2 is smaller than 3, you get a decimal point right after 0.
After the decimal point, you can add a zero, making it ‘2.0’.
Now, see how many times 3 goes into 20, which is 6 times, and you get 18.
Subtract 18 from 20, which gives you a remainder of 2.
Add another 0 after 20 making it ‘20.0’.
Repeat the division process.
This process continues until you have a remainder of 0 or until you have a recurring (repeating) decimal.
How Do You Convert a Fraction to a Percentage?
Step 1) Understanding Percentages
Before we start converting, let’s understand what percentages are. A percentage is a way of expressing a number as a fraction of 100. The term ‘percent’ literally means ‘per hundred.’ So, if you’re converting a fraction into a percentage, you’re changing the denominator to 100.
Step 2) Converting the Fraction to a Decimal
The first step in converting a fraction to a percentage is turning it into a decimal. You do this by dividing the numerator (the top number) by the denominator (the bottom number). For example, if you have the fraction 3/4, divide 3 by 4, and you get the decimal 0.75.
If you’re not able to do this division in your head, don’t worry. You can use long division to help you.
Step 3) Converting the Decimal to a Percentage
Once you have the decimal, the next step is to convert it into a percentage. To do this, you simply multiply the decimal by 100. So, taking the previous example, if you multiply 0.75 by 100, you get 75. Don’t forget to add the ‘%’ sign at the end to indicate that your answer is a percentage. So, 3/4 is equal to 75%.
Step 4) Simplifying If Necessary
Sometimes you’ll end up with a decimal percentage, such as 66.666…% when converting 2/3. You can choose to round this to the nearest whole number or leave it as a decimal, depending on the level of precision you need.