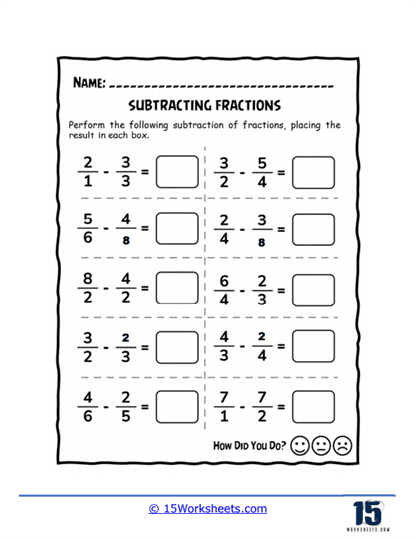
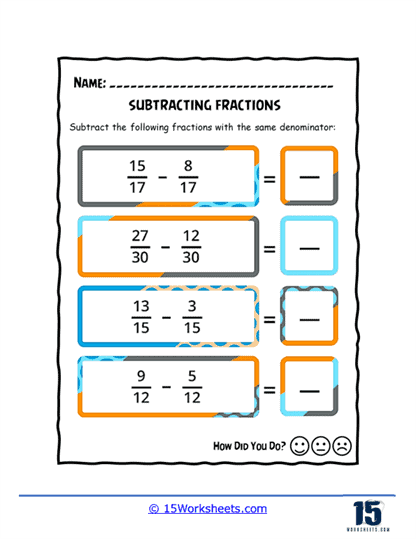
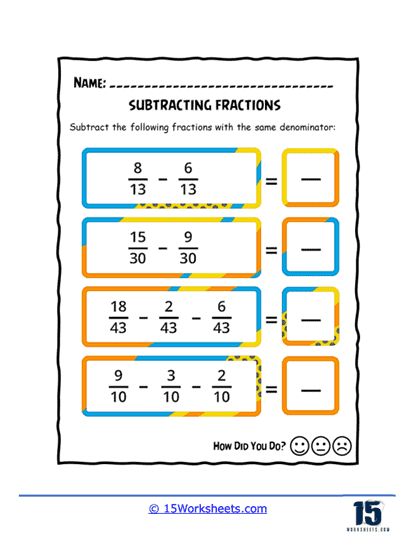
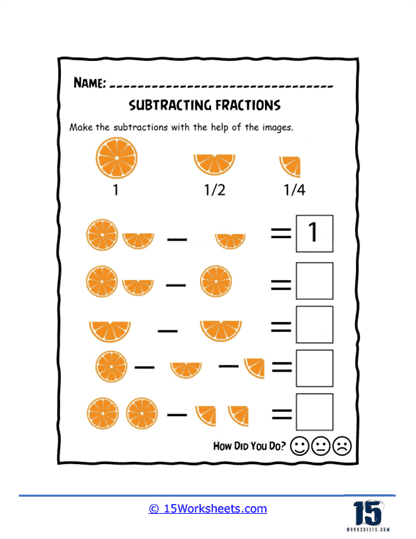
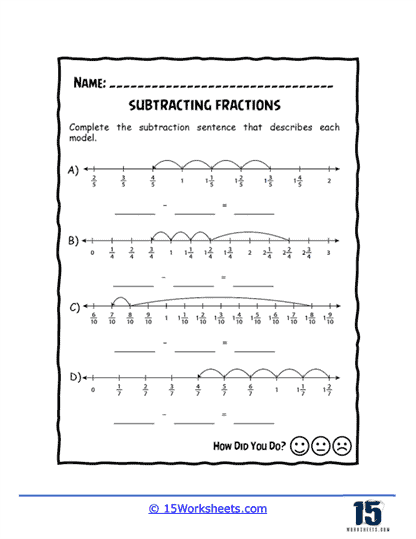
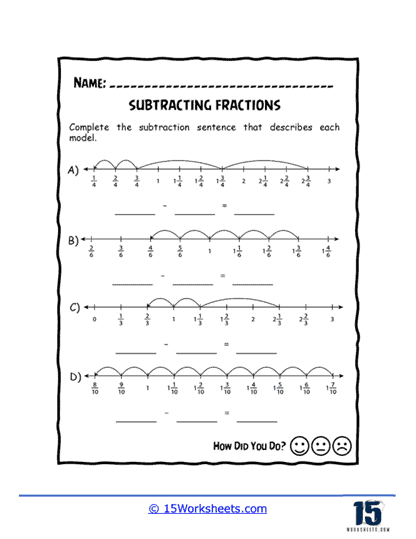
Subtracting Fractions Worksheets
All About These 15 Worksheets
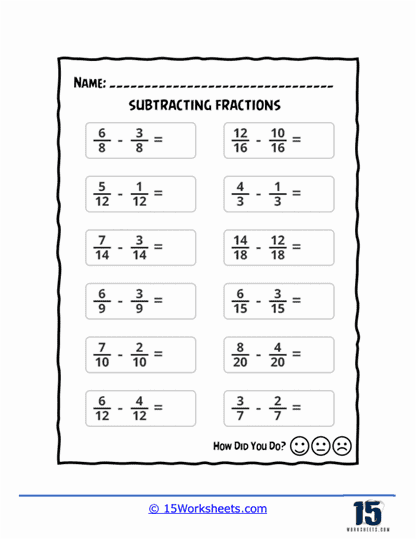
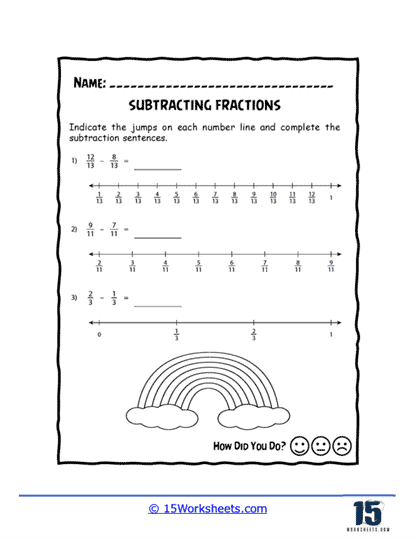
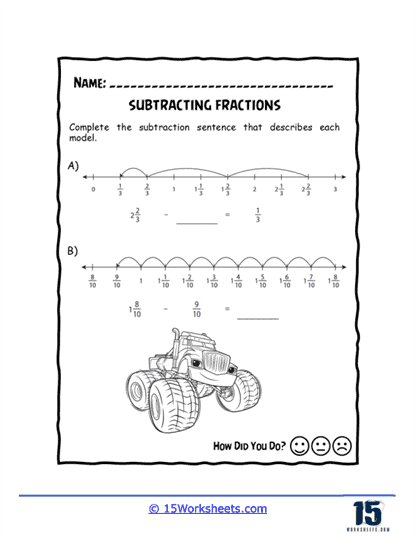
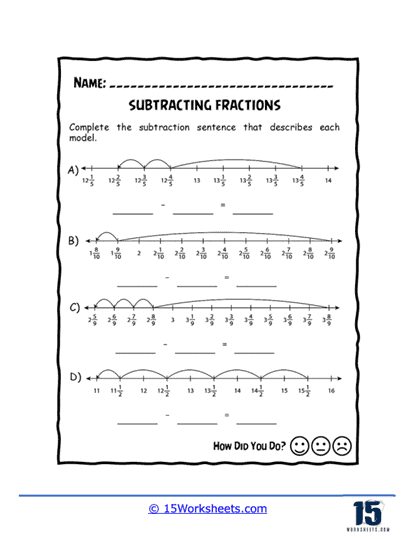
This series of worksheets on subtracting fractions is a comprehensive and effective set of materials designed to help students master this essential math concept. Subtracting fractions is a critical skill that forms the foundation of many more advanced math topics, and these worksheets can provide students with ample practice and guidance to master this skill.
The worksheets are organized into several different sections, each of which focuses on a specific aspect of subtracting fractions. These sections include basic subtraction, subtracting mixed numbers, subtracting fractions with unlike denominators, and subtracting fractions with borrowing. The exercises are designed to be both challenging and engaging, with a variety of problems ranging from basic to advanced difficulty. The worksheets are suitable for use in a classroom setting or as homework, and they can be easily customized to meet the needs of individual students.
Overall, this series of worksheets on subtracting fractions is an excellent resource for learners of all ages and skill levels. With clear instructions, engaging problems, and ample practice opportunities, these materials are sure to help students master this critical math concept and build a strong foundation for future learning.
How to subtract fractions
Subtracting fractions may seem a bit challenging at first, but with the right approach, it can be a straightforward process. Here’s a step-by-step process on how to subtract fractions that teachers can guide their students through.
Step 1: Find a common denominator.
The first step is to make sure the fractions have a common denominator. If they don’t already have one, you’ll need to find the least common denominator (LCD). To do this, you’ll need to identify the factors of the denominators and find the least common multiple (LCM) of these factors. The LCM is the LCD.
Step 2: Convert the fractions.
Once you’ve found the common denominator, convert each fraction so that they have the same denominator. To do this, multiply both the numerator and denominator of each fraction by the same factor. The factor is usually the denominator of the other fraction.
Step 3: Subtract the numerators.
Now that the fractions have the same denominator, you can simply subtract the numerators. Be sure to keep the denominator the same. For example, to subtract 2/5 from 3/4, you would find the common denominator of 20, convert both fractions to have a denominator of 20 (3/4 becomes 15/20 and 2/5 becomes 8/20), and then subtract the numerators: 15/20 – 8/20 = 7/20.
Step 4: Simplify the answer.
Finally, simplify the resulting fraction, if possible, by dividing both the numerator and denominator by their greatest common factor. For example, the difference of 3/4 and 2/5 is 7/20, which cannot be simplified any further.
Remember that if you’re subtracting mixed numbers, you’ll need to convert them to improper fractions first before following the above steps. With practice, you’ll be able to subtract fractions quickly and accurately.