Adding Fractions Worksheets
About These 15 Worksheets
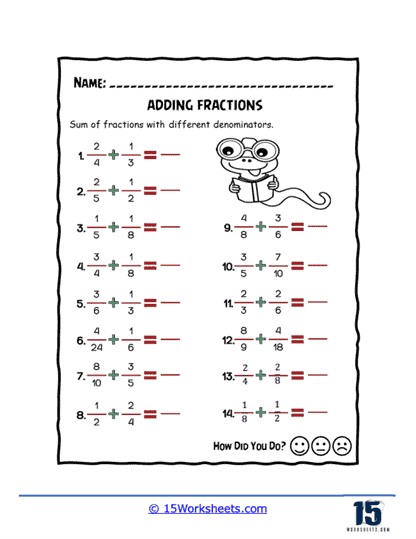
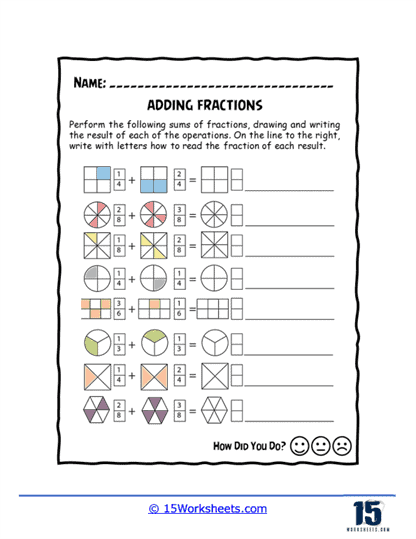
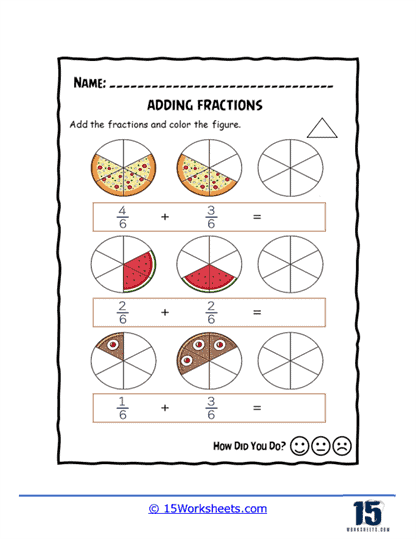
Adding fractions worksheets will help students practice and improve their skills in adding fractions. These worksheets contain a series of problems or exercises that involve adding fractions with like or unlike denominators. The problems may vary in complexity, starting from simple fractions with common denominators to more challenging ones with different denominators.
These worksheets serve as valuable tools for reinforcing the concept of adding fractions, allowing students to gain proficiency and confidence in this fundamental mathematical skill. They provide ample practice opportunities to ensure that students grasp the underlying principles and become adept at adding fractions accurately and efficiently.
How to Add Fractions
Adding fractions involves combining two or more fractions with the same or different denominators. Here’s a step-by-step guide on how to add fractions:
Step 1) Check the Denominators – Look at the denominators of the fractions you’re adding. If they are the same, you can skip to step 3. If they are different, proceed to step 2.
Step 2) Find a Common Denominator – In order to add fractions with different denominators, you need to find the least common denominator (LCD) – the smallest multiple that both denominators share. To find the LCD:
a. List the multiples of each denominator.
b. Identify the smallest multiple that appears in both lists.
c. Use this multiple as your common denominator.
For example, if you’re adding 1/4 and 1/6:
- Multiples of 4: 4, 8, 12, 16, 20, …
- Multiples of 6: 6, 12, 18, 24, 30, …
The smallest common multiple is 12, so the LCD is 12.
Step 3) Convert the Fractions to Equivalent Fractions with the Common Denominator – To do this, divide the common denominator by the original denominator and multiply both the numerator and denominator of the original fraction by the result.
For example, to convert 1/4 and 1/6 to equivalent fractions with the LCD of 12:
- For 1/4: (12 ÷ 4 = 3) → 1/4 × 3/3 = 3/12
- For 1/6: (12 ÷ 6 = 2) → 1/6 × 2/2 = 2/12
Now, you have the equivalent fractions: 3/12 and 2/12.
Step 4) Add the Numerators – Keep the common denominator and add the numerators of the equivalent fractions.
In our example: 3/12 + 2/12 = (3 + 2)/12 = 5/12
So, 1/4 + 1/6 = 5/12.
Step 5) Simplify The Result (if possible) – If the resulting fraction can be simplified further, divide both the numerator and the denominator by their greatest common divisor (GCD).
In our example, the fraction 5/12 is already in its simplest form, so no further simplification is needed.
Remember to always express your final answer in its simplest form.
Example #1 – 3/6 + 2/6
We will rewrite it as: 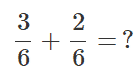
Since the denominators are the same (6). We would just add the numerators in this manner:
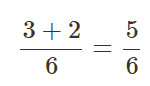
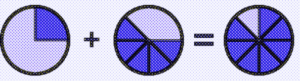
Take a look at this using visual models: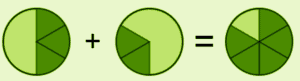
Example #2- 1/4 + 5/8
We will rewrite it as: 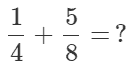
Since the denominators are different (4, 8), we need to make have a common denominator. Since 8 is a multiple of 4 (4 x 2), we can multiple that fraction by 2 over 2. This would look like this:
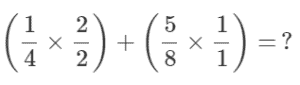
Once we condense all of this math, we are left with:
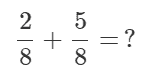
We now have common denominators and just add the numerators. In this way:
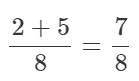
Therefore 1/4 + 5/8 = 7/8.
Take a look at this using visual models: