Ordering Fractions Worksheets
About These 15 Worksheets
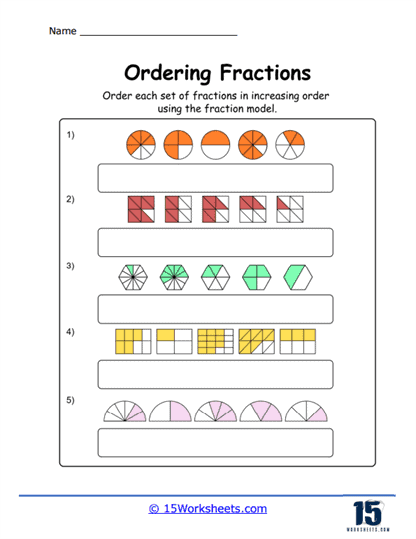
Ordering fractions worksheets are educational tools geared toward teaching students how to sequence fractions based on their relative values, moving from smallest to largest or vice versa. Mastery of this concept is foundational for understanding more complex arithmetic and algebraic operations involving fractions later in one’s mathematical journey.
Types of Exercises
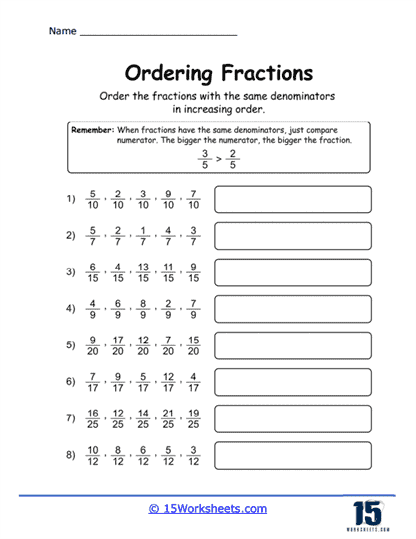
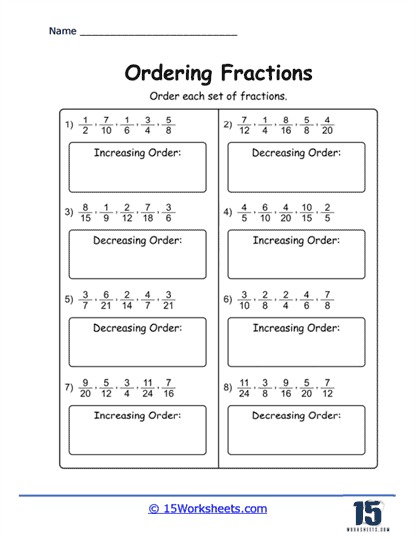
Basic Ordering with Like Denominators – This is often the starting point for students learning about ordering fractions. In these exercises, students are given a series of fractions that all have the same denominator and are asked to order them. This introduces students to the idea that when the denominators are the same, ordering is straightforward; the fraction with the larger numerator is greater.
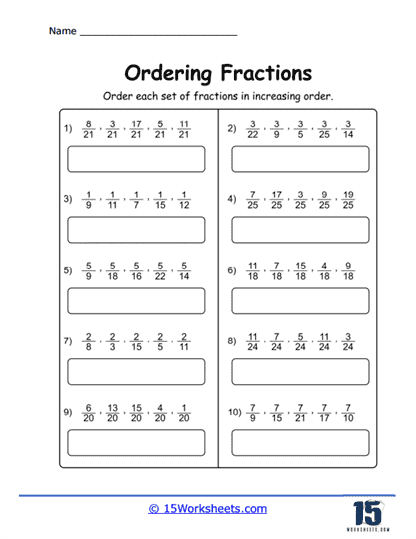
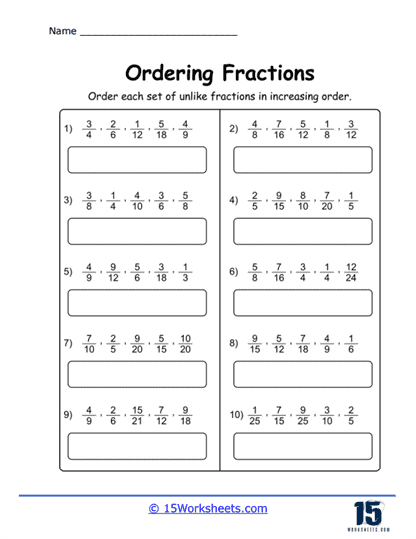
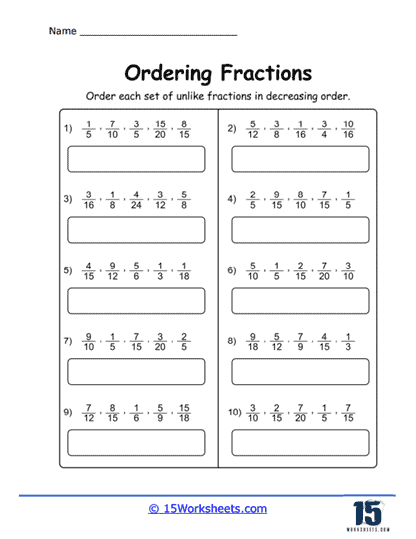
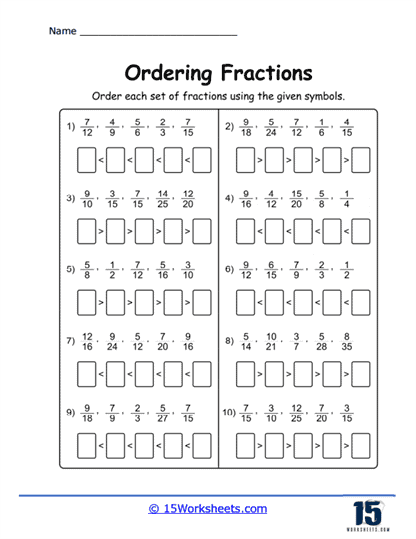
Ordering with Unlike Denominator – A more complex task where students order fractions with different denominators. This often requires them to either find a common denominator or convert the fractions to decimals. This teaches students about the relative sizes of different fractions and provides practice in finding common denominators or converting fractions to decimals.
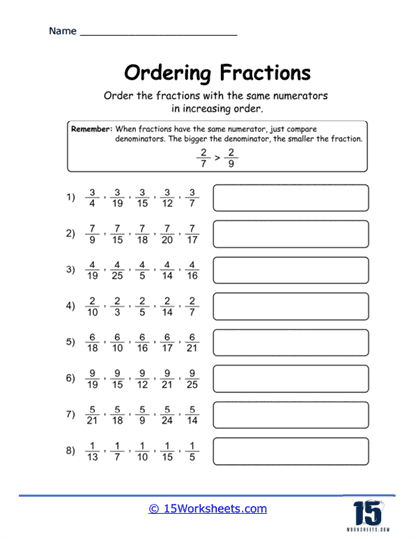
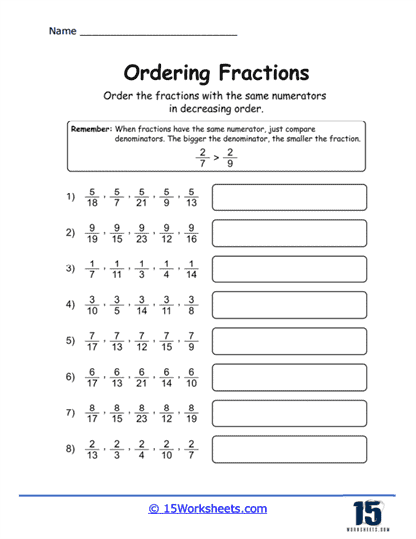
Using Benchmark Fractions – Benchmark fractions (like 1/2) are used as reference points to help order a list of fractions. This approach helps students develop intuition about the relative sizes of fractions. By comparing other fractions to known benchmarks, students can make educated estimations about their size.
Comparing Fractions to Whole Numbers – Students are given fractions and whole numbers and are asked to order the combined list. This helps students understand the relationship between fractions and whole numbers and reinforces the concept that fractions can be greater than one.
From ordering fractions worksheets, students gain a multitude of valuable insights and skills. Firstly, they develop an enhanced number sense. The sequencing exercises in these worksheets bolster a student’s inherent understanding of numbers and how they relate in size to one another.
Students also encounter exercises that blend fractions, decimals, and percentages, they become adept at transitioning between different number forms. This equips them for both advanced mathematical tasks and real-world scenarios where numbers can appear in a variety of formats. Additionally, students are honed in strategic thinking, especially when faced with decisions such as whether to determine a common denominator, utilize a benchmark fraction, or switch to a decimal format.
The real-world problems incorporated into these worksheets underscore the daily practicality and importance of ordering fractions effectively. Lastly, it’s worth noting that these worksheets do more than teach mere fraction ordering. They lay the groundwork for more intricate mathematical operations, building a robust foundation for getting more comfortable with math in general.
How Do You Order Fractions?
Ordering fractions is a crucial skill in arithmetic and is often introduced to students early in their study of fractions. Comparing and ordering fractions becomes easier with a clear understanding of equivalent fractions and common denominators. Here’s how you can order fractions from least to greatest and from biggest to smallest:
a) Same Denominator – If fractions have the same denominator, it’s straightforward.
Compare the numerators directly.
For Least to Greatest: Place the fraction with the smallest numerator first.
For Biggest to Smallest: Place the fraction with the largest numerator first.
Example: 2/7, 5/7, 1/7
Ordered from Least to Greatest: 1/7, 2/7, 5/7
Ordered from Biggest to Smallest: 5/7, 2/7, 1/7
b) Different Denominators – For fractions with different denominators, there are a few methods:
1) Common Denominator Method
Find the least common denominator (LCD) for the fractions.
Convert each fraction to an equivalent fraction with the LCD as the new denominator.
Once they all have the same denominator, compare the numerators as described above.
Example: 1/3, 1/4, 2/5
LCD = 60
Convert: 20/60, 15/60, 24/60
Ordered from Least to Greatest: 15/60 (or 1/4), 20/60 (or 1/3), 24/60 (or 2/5)
Ordered from Biggest to Smallest: 24/60 (or 2/5), 20/60 (or 1/3), 15/60 (or 1/4)
2) Cross Multiplication Method
When comparing two fractions – Cross-multiply the fractions and compare the results.
For Least to Greatest: The fraction corresponding to the smaller cross-product comes first.
For Biggest to Smallest: The fraction corresponding to the larger cross-product comes first.
Example: To compare 3/4 and 5/6
Cross-multiplication: 3×6 = 18 and 5×4 = 20
3/4 < 5/6 because 18 < 20
3) Decimal Conversion Method – Convert each fraction to a decimal.
Compare the decimal values.
Example: 1/3, 1/4, 2/5
Convert: 0.333…, 0.25, 0.4
Ordered from Least to Greatest: 0.25 (or 1/4), 0.333… (or 1/3), 0.4 (or 2/5)
Ordered from Biggest to Smallest: 0.4 (or 2/5), 0.333… (or 1/3), 0.25 (or 1/4)
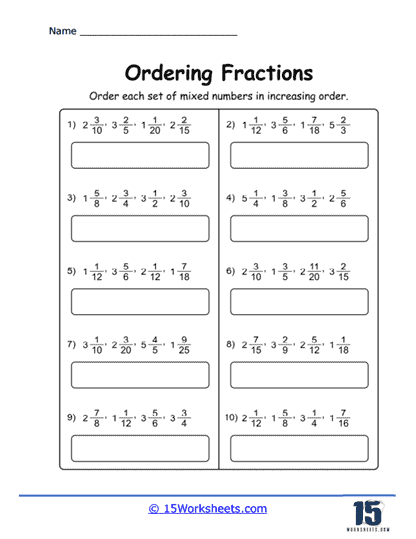
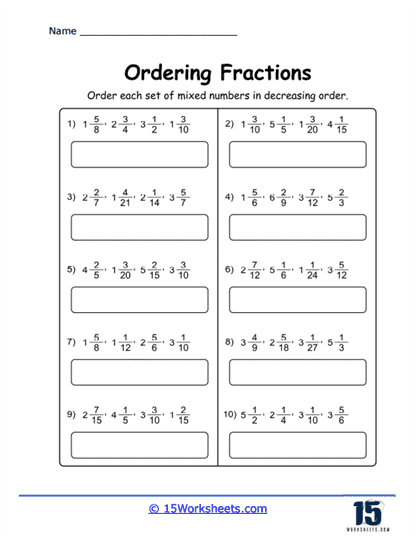
c) Mixed Numbers – For mixed numbers, first compare the whole number part.
If the whole numbers are the same, then compare the fractional parts using methods described above.
Example: 3 1/2, 2 3/4, 3 1/4
Ordered from Least to Greatest based on whole numbers and then fractions: 2 3/4, 3 1/4, 3 1/2
Ordered from Biggest to Smallest: 3 1/2, 3 1/4, 2 3/4