Simplifying Fractions Worksheets

About These 15 Worksheets

A fraction, as you might know, represents a part of a whole. It has two parts – the numerator (the top number) that shows how many parts we have, and the denominator (the bottom number) that indicates the total number of equal parts. For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator. This fraction means we have 3 parts out of 4 total equal parts.

So, what does it mean to simplify or reduce fractions? Well, think of it like simplifying a big, heavy backpack. If you’re carrying around a backpack filled with 4 books, but you realize you have 2 copies of the same book, you can remove the extra to make your backpack lighter. Similarly, in math, we simplify fractions to their smallest, most basic form. This makes them easier to understand and work with.

That’s where these worksheets come into play. They provide exercises that guide you through the process of simplifying fractions. Here are some examples of the different types of exercises you will encounter:

1. Recognizing Simplicity: “Reduce the Fractions,” “Lowest Terms,” “Circle the Lowest“

Kids face the familiar trio: “Reduce the Fractions,” “Lowest Terms,” and “Circle the Lowest.” These are the fraction equivalent of clean-the-room chores-necessary, slightly tedious, but undeniably satisfying when everything’s neat. Students systematically chip away at numerator and denominator until the pair is in “lowest terms,” sometimes circling the simplest version like they’ve spotted Bigfoot. It’s all about instinctively asking, “Can you go smaller, buddy?”-and then doing it.

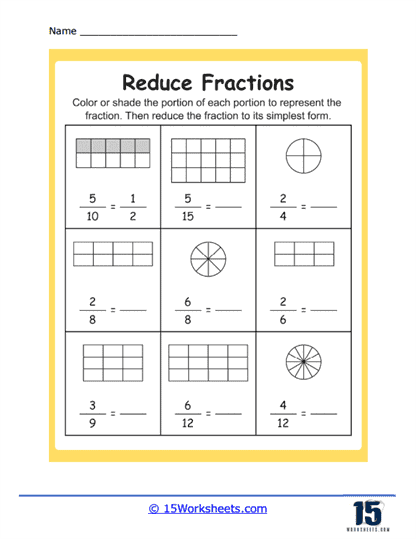
2. Simplification Techniques: “Simplifying Fractions,” “Simplest Form,” “Simplifying Fractional Images“

Next, the curriculum dives deeper with “Simplifying Fractions,” “Simplest Form,” and the visually charming “Simplifying Fractional Images.” They nudge learners out of mechanical reducing and toward seeing why it works, even applying it to tiny pie-slice cartoons or shaded bars. It’s the difference between regimented drills and suddenly thinking, “Oh-I get it,” when you turn a 9/27 illustration into something that resembles chewing gum-but mathematically edible.

3. Beyond the Basics: “Reduce Mixed Numbers,” “Reducing Improper Fractions,” “Reducing Dot Fractions“

Once comfort sets in, students meet the fraternal triplet of trickier beasts: “Reduce Mixed Numbers,” “Reducing Improper Fractions,” and “Reducing Dot Fractions.” Suddenly, whole numbers waltz with fractions (“3 ½”), upside‑down champions appear, and dot‑diagram puzzles mimic a kindergarten connect‑the‑dots but sneak in simplification practice. It’s strategic mental yoga-helping learners realize reducing doesn’t stop at “regular” fractions; it’s a universal life‑skill, like knowing how to fold a fitted sheet (almost).

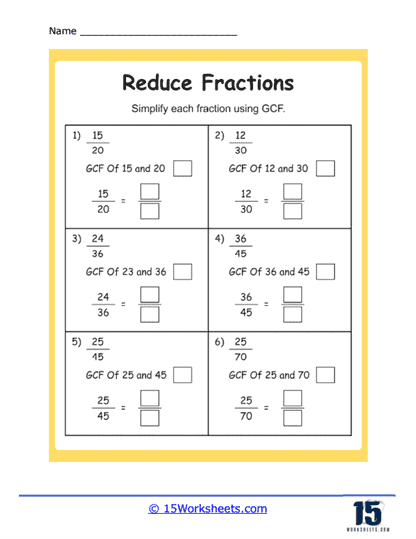
4. Deeply Mathematical:  “Using GCF“

Then comes the brain-buster duo: “Using GCF”. This ask students to identification the greatest common factor before slashing numerators and denominators-no shortcuts. It’s the fraction version of detective work: find the prime suspects, check the evidence (multiples), and pronounce, “Ha! GCF 6!” Then reduce 12/18 to the smug elegance of 2/3. Overthinkers rejoice; once kids see GCF, fractions become a game of number‑themed Sudoku.

5. Out of the Box Fun: “2 Equivalent Fractions,” “Color Code Puzzle,” “Reduce and Shade,” “Simplifying Fractions Cryptogram“

The creative crescendo: “2 Equivalent Fractions,” “Color Code Puzzle,” “Reduce and Shade,” and the cryptic “Simplifying Fractions Cryptogram.” Here, kids pair fractions to see if they’re secretly twins. They color‑match puzzles as if fraction‑printers threw a rave. “Reduce and Shade” feels like arts‑and‑crafts meets algebra-shade those simplified squares and reveal hidden shapes. The cryptogram tops it off with spy‑level intrigue: decode messages by simplifying fractions. It’s fraction espionage for the budding math agent.

How Do You Simplify a Fraction?

Simplifying a fraction means reducing it to its simplest form, where the numerator (the number on top) and the denominator (the number at the bottom) have no common factors except 1.

To simplify a fraction, follow these steps:

Find the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), of the numerator and the denominator. This is the largest number that can evenly divide both the numerator and the denominator.

Divide both the numerator and the denominator by their GCD. The fraction you get as a result is the simplified form.

Here are three examples to help you understand this better:

Example 1 – Simplify 8/12

First, find the GCD of 8 and 12. The factors of 8 are 1, 2, 4, and 8, and the factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest number that appears in both lists is 4, so the GCD is 4.

Now, divide both the numerator and the denominator by 4. Doing this gives you 8 ÷ 4 / 12 ÷ 4 = 2/3.

So, the simplified form of 8/12 is 2/3.

Example 2 – Simplify 15/25

The GCD of 15 and 25 is 5 (since both 15 and 25 can be divided evenly by 5).

Divide both the numerator and the denominator by 5 – 15 ÷ 5 / 25 ÷ 5 = 3/5.

So, the simplified form of 15/25 is 3/5.

Example 3 – Simplify 18/27

The GCD of 18 and 27 is 9 (since both 18 and 27 can be divided evenly by 9).

Divide both the numerator and the denominator by 9 – 18 ÷ 9 / 27 ÷ 9 = 2/3.

So, the simplified form of 18/27 is 2/3.