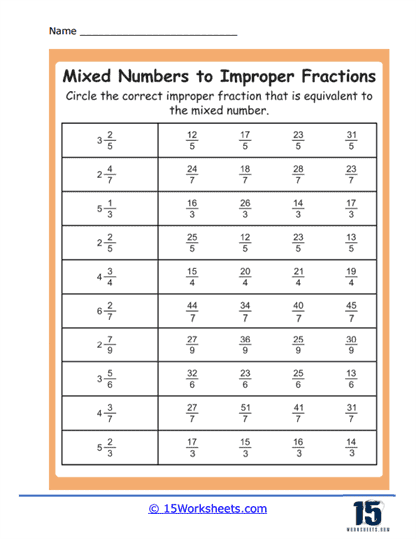
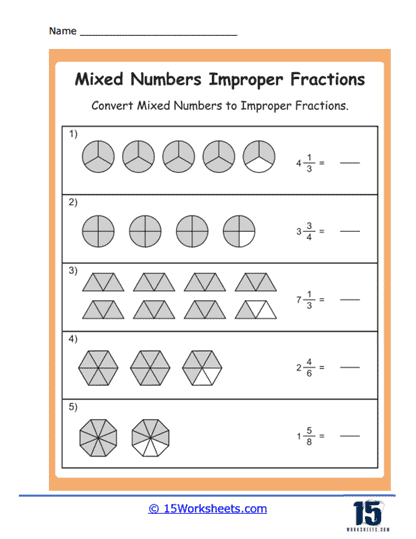
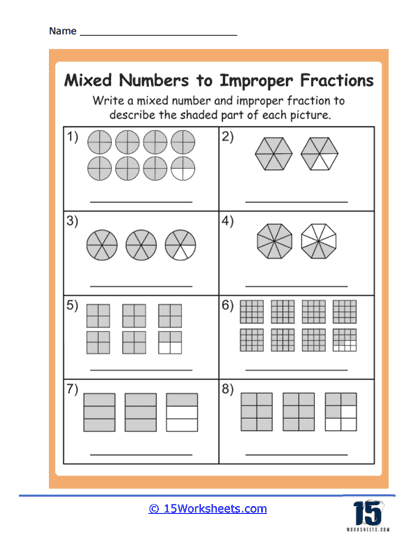
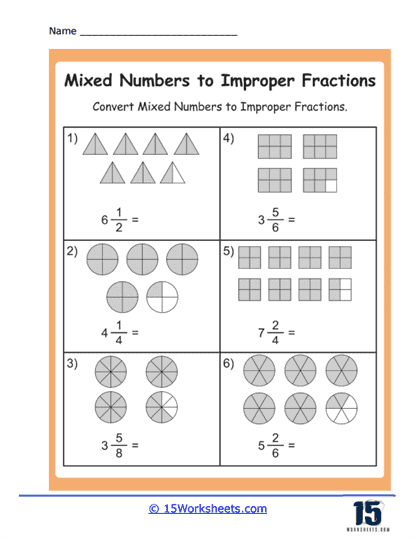
Mixed Numbers to Improper Fractions Worksheets
About These 15 Worksheets
These worksheets will help you understand the process of converting mixed numbers into improper fractions. It’s important to first grasp what mixed numbers and improper fractions are before diving into the content of these worksheets.
A mixed number is a number that includes both a whole number and a fraction, such as 2 1/2 or 3 3/4. An improper fraction, on the other hand, is a fraction where the numerator (the top number) is equal to or larger than the denominator (the bottom number), like 5/4 or 7/3.
The worksheets focused on converting mixed numbers to improper fractions are designed to help you master this skill. Understanding how to switch between these two forms can provide a more comprehensive understanding of fractions and their relationship to whole numbers. It can also simplify calculations and make it easier to work with fractions in certain mathematical or real-world scenarios.
There are several types of problems you might find on these worksheets:
Basic Conversion Problems – These problems directly ask you to convert a given mixed number into an improper fraction. For example, “Convert the mixed number 2 1/2 to an improper fraction.”
Reverse Conversion Problems – These problems might ask you to convert an improper fraction back into a mixed number. Although the main focus is on converting mixed numbers to improper fractions, these problems reinforce your understanding of the relationship between the two.
So why is this skill important? Converting mixed numbers to improper fractions can simplify the process of mathematical operations like addition, subtraction, multiplication, and division. It also forms the foundation for understanding more complex mathematical concepts in algebra and calculus. Further, the process of conversion between mixed numbers and improper fractions enhances your numerical fluency and flexibility in manipulating numbers, which are critical skills in mathematics.
Let’s now discuss some examples of when this skill might come in handy in your daily life:
Cooking and Baking – When you’re following a recipe and need to double or halve the measurements, converting mixed numbers to improper fractions can make calculations much simpler.
Sports – If you’re playing a game where scores are kept as fractions (like some card games), it might be easier to add scores if you convert mixed numbers to improper fractions.
Shopping – Suppose you’re buying multiple items priced in fractions of a dollar. Converting the prices to improper fractions can make it easier to calculate the total cost.
School Projects – If you’re working on a project that requires measurement, such as building a model, converting mixed numbers to improper fractions can simplify the process of adding or subtracting different measurements.
How Do You Perform This Skill?
Converting mixed numbers to improper fractions is a key skill in understanding and working with fractions. The process involves three main steps:
Multiply the Whole Number by the Denominator – In a mixed number, you have a whole number and a fraction. Begin by multiplying the whole number part by the denominator of the fraction.
Add the Numerator – Next, add the result from step 1 to the numerator of the fraction.
Write the Improper Fraction – The resulting number becomes the numerator of the improper fraction, and the denominator stays the same as in the original mixed number.
Now, let’s see some examples to make this clearer.
Example 1 – Convert the mixed number 2 1/3 to an improper fraction.
Multiply the Whole Number by the Denominator – 2 times 3 equals 6.
Add the Numerator – 6 plus 1 equals 7.
Write the Improper Fraction – Therefore, 2 1/3 as an improper fraction is 7/3.
Example 2 – Convert the mixed number 4 2/5 to an improper fraction.
Multiply the Whole Number by the Denominator – 4 times 5 equals 20.
Add the Numerator – 20 plus 2 equals 22.
Write the Improper Fraction – Therefore, 4 2/5 as an improper fraction is 22/5.
Example 3 – Convert the mixed number 3 3/4 to an improper fraction.
Multiply the Whole Number by the Denominator – 3 times 4 equals 12.
Add the Numerator – 12 plus 3 equals 15.
Write the Improper Fraction – Therefore, 3 3/4 as an improper fraction is 15/4.
Example 4 – Convert the mixed number 5 1/2 to an improper fraction.
Multiply the Whole Number by the Denominator – 5 times 2 equals 10.
Add the Numerator – 10 plus 1 equals 11.
Write the Improper Fraction – Therefore, 5 1/2 as an improper fraction is 11/2.
Example 5 – Convert the mixed number 6 4/7 to an improper fraction.
Multiply the Whole Number by the Denominator – 6 times 7 equals 42.
Add the Numerator – 42 plus 4 equals 46.
Write the Improper Fraction – Therefore, 6 4/7 as an improper fraction is 46/7.