Reciprocals Worksheets
About These 15 Worksheets
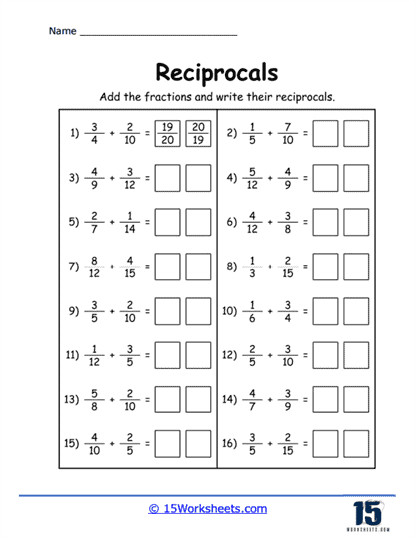
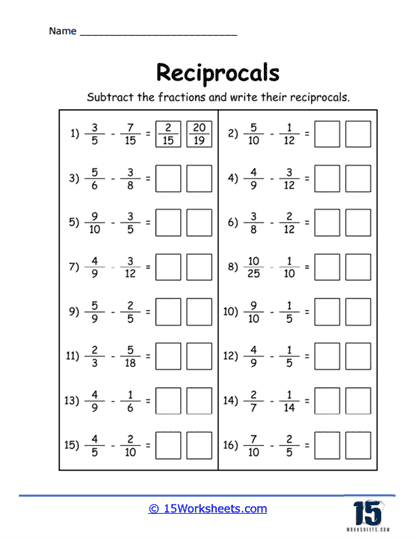
In mathematical terms, the reciprocal of a whole number is 1 divided by that number. For instance, the reciprocal of 5 is 1/5, and the reciprocal of 1/3 is 3. In terms of fractions reciprocals are when the numerator and the denominator switch places for instance the reciprocal of 2/5 is 5/2.
These worksheets are designed to help students grasp this concept and its applications. These worksheets systematically introduce students to the idea, its properties, and its wide-ranging applications. With a careful blend of basic drills, practical applications, and challenging exercises, these worksheets can help students attain a deep and lasting understanding of reciprocals, setting them up for success in more advanced mathematical topics. Understanding reciprocals is essential for simplifying complex fractions, working with rational expressions, and solving equations.
Types of Exercises
Basic Identification – Students are provided with a list of numbers (both whole numbers and fractions) and are tasked with identifying their reciprocals. This foundational exercise helps students familiarize themselves with the basic concept of reciprocals.
Simplifying Fractions using Reciprocals – Students are given complex fractions (fractions within fractions) and must use the reciprocal to simplify them. This practice enhances understanding of how reciprocals can simplify complex mathematical expressions and helps students become comfortable with manipulating fractions
Exploring Properties of Reciprocals – Exercises that delve into properties like the product of a number and its reciprocal being 1. Through hands-on practice, students internalize essential mathematical properties, leading to a more profound understanding of the subject.
Multiplicative Inverse – Exercises that introduce the term “multiplicative inverse” as another name for the reciprocal and explore its implications. It expands students’ mathematical vocabulary and deepens their conceptual understanding.
How to Determine Reciprocals
The reciprocal of a number is obtained by dividing 1 by that number. In simpler terms, the reciprocal of a number is its multiplicative inverse. The product of a number and its reciprocal is always 1 (except for 0, which doesn’t have a reciprocal). Here’s how to determine the reciprocal of various types of numbers:
a) Whole Numbers and Integers – For any non-zero whole number or integer x, its reciprocal is 1/x.
Examples:
The reciprocal of 5 is 1/5.
The reciprocal of -3 is – 1/3.
b) Fractions – For any fraction a/b where a and b are integers and a is not zero, its reciprocal is b/a.
Examples:
The reciprocal of 4/6 is 6/4.
The reciprocal of -5/8 is -8/5.
The only number that doesn’t have a reciprocal is 0. Since dividing by zero is undefined in mathematics, 0 doesn’t have a multiplicative inverse. If you attempt to find the reciprocal of zero, it will result in an undefined operation.