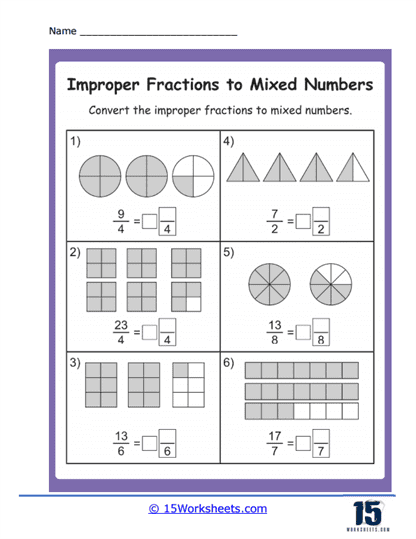
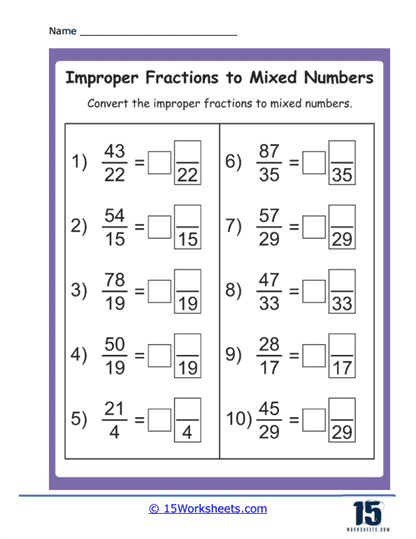
Improper Fractions to Mixed Numbers Worksheets
About These 15 Worksheets
These worksheets were designed by our teachers to help you, as a middle school student, understand and master the process of changing improper fractions into mixed numbers. But before we delve into what these worksheets encompass, let’s first understand some key terms.
An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 7/3 or 5/5 are improper fractions.
A mixed number, on the other hand, is a whole number combined with a proper fraction (where the numerator is less than the denominator). An example of a mixed number is 2 1/3, which includes the whole number 2 and the fraction 1/3.
The worksheets focused on converting improper fractions to mixed numbers provide you with the practice needed to become proficient in this skill. Understanding this conversion is important because it allows you to express fractions in a format that can be easier to comprehend and work with.
There are several types of problems that you might encounter on these worksheets. Here are a few examples:
Basic Conversion Problems – These are straightforward problems where you’re given an improper fraction and asked to convert it to a mixed number. For example, you might see a problem like – “Convert the improper fraction 7/3 to a mixed number.”
Reverse Conversion Problems – These are problems where you’re given a mixed number and asked to convert it to an improper fraction. Although the primary focus is on converting improper fractions to mixed numbers, these reverse problems help cement your understanding of the relationship between the two.
Now, why is this skill important? Converting improper fractions to mixed numbers helps clarify the concept of fractions and their relation to whole numbers. Mixed numbers are often easier to understand and visualize. For example, if you’re told you have 7/3 of a pizza, it might be hard to picture. But if you convert that to 2 1/3 pizzas, it becomes much clearer. This skill also forms the basis for more advanced mathematical concepts, such as algebra and calculus, making it an essential part of your mathematical foundation.
The skill of converting improper fractions to mixed numbers is also very applicable to your daily life. Here are some instances where this skill might come in handy:
Cooking and Baking – Recipes often involve fractions, and sometimes, they can be improper fractions. Being able to convert these to mixed numbers can make it easier for you to measure ingredients accurately.
Shopping – Imagine you’re at a fabric store, and you’ve bought 5/2 yards of fabric for a sewing project. Converting this to a mixed number (2 1/2) can make it easier for you to visualize how much fabric you actually have.
Home Projects – Suppose you’re building a birdhouse, and a plank of wood measures 11/2 feet. Converting this to a mixed number can help you better understand the measurements you’re working with.
Sports – If you’re into running and you ran 13/5 miles today, converting this to a mixed number can give you a clearer picture of the distance you covered.
How Do You Convert Improper Fractions to Mixed Numbers?
Converting an improper fraction to a mixed number is a fairly straightforward process. It involves dividing the numerator (the top number) by the denominator (the bottom number) to get a whole number and a remainder. The whole number becomes the integral part of the mixed number, and the remainder forms the numerator of the fractional part.
Here’s the process in detail:
Divide the Numerator by the Denominator – In an improper fraction, the numerator is greater than the denominator. So, divide the numerator by the denominator.
Identify the Whole Number – The quotient (the result of your division) is the whole number part of the mixed number.
Identify the Remainder – The remainder of your division becomes the new numerator in the fractional part of the mixed number.
Write the Mixed Number – The mixed number is written as the whole number from step 2 and a fraction formed by the remainder (from step 3) over the original denominator.
Let’s go through a few examples to illustrate this process:
Example 1 – Convert the improper fraction 7/3 to a mixed number.
Divide the Numerator by the Denominator – 7 divided by 3 is 2 remainder 1
Identify the Whole Number – The quotient is 2.
Identify the Remainder – The remainder is 1.
Write the Mixed Number – Therefore, 7/3 as a mixed number is 2 1/3.
Example 2 – Convert the improper fraction 11/4 to a mixed number.
Divide the Numerator by the Denominator – 11 divided by 4 is 2 remainder 3.
Identify the Whole Number – The quotient is 2.
Identify the Remainder – The remainder is 3.
Write the Mixed Number – Therefore, 11/4 as a mixed number is 2 3/4.
Example 3 – Convert the improper fraction 8/5 to a mixed number.
Divide the Numerator by the Denominator – 8 divided by 5 is 1 remainder 3.
Identify the Whole Number – The quotient is 1.
Identify the Remainder – The remainder is 3.
Write the Mixed Number – Therefore, 8/5 as a mixed number is 1 3/5.