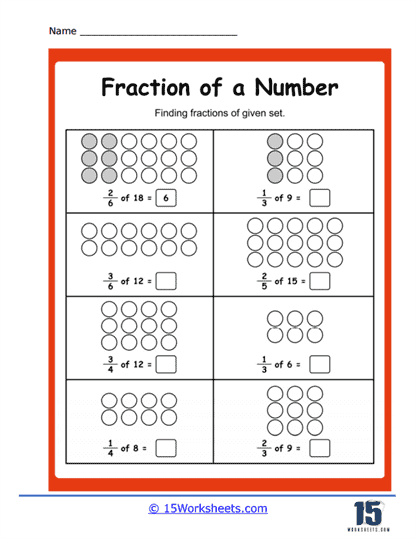
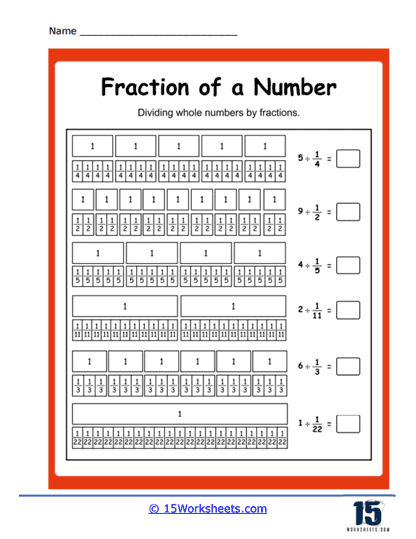
Fractions of a Whole Number Worksheets
About These 15 Worksheets
These worksheets are filled with exercises that are specifically designed to help you understand how fractions work in relation to whole numbers. They cover essential mathematical principles that will help you appreciate the use of fractions in everyday scenarios.
One of the first things to understand about these worksheets is that they are based on the concept of fractions. Fractions are numbers that represent parts of a whole. For example, if you divide an apple into four equal parts, each part is represented by the fraction 1/4. When you look at a whole number, such as 10, and you want to find out what 1/4 of that 10 is, you’re using the skill of finding fractions of a whole number.
The worksheets generally contain problems of various types to provide a comprehensive understanding of this skill. The first type of problem you will often see is straightforward calculations where you’re asked to find a certain fraction of a whole number. For example, you might be asked – “What is 1/2 of 20?” or “What is 3/4 of 24?”
Another common type of problem you might encounter is word problems. These problems involve a scenario that requires you to use fractions to find a solution. For example, “Johnny has 30 marbles. He gives 2/3 of his marbles to his friend. How many marbles does he give away?” Word problems help improve your ability to apply math in real-world situations.
There can also be problems where you’re given a fraction of a whole number and asked to find the original whole number. For example, “3/4 of a number is 15. What is the number?” This kind of problem can help strengthen your understanding of the relationship between fractions and whole numbers.
Understanding fractions of a whole number is a crucial mathematical skill because it forms the basis of many more advanced topics in math. For instance, understanding fractions and how they relate to whole numbers is fundamental in algebra, calculus, and statistics, among other areas of math. It also improves your problem-solving skills and ability to think logically, which are valuable skills to have in all aspects of life.
In your daily life, the skill of finding fractions of a whole number is used in a variety of ways. Let’s go through a few examples to help you understand better.
Cooking and Baking – If you enjoy cooking or baking, or even just following a recipe, you’re already using fractions. Recipes usually involve measurements like “1/2 cup of sugar” or “1/4 teaspoon of salt.” When you’re doubling a recipe or cutting it in half, you’re working with fractions of whole numbers.
Money – Imagine you’re at a store, and there’s a 50% off sale (which is the same as 1/2 off). If an item originally costs $20, how much will it cost after the discount? You would need to find 1/2 of $20 to determine the new price.
Time Management – Fractions can also help you manage your time better. Suppose you have an hour (60 minutes) to do your homework, and you want to spend 1/3 of that time on math, you’ll need to figure out what 1/3 of 60 minutes is.
Sports – If you’re into sports, you might use fractions to understand statistics. For example, if a basketball player makes 2 out of 3 free throws, that’s the same as saying they make 2/3 of their shots.
How Do You Find the Fraction of a Whole Number?
Finding a fraction of a whole number is a fundamental skill in mathematics. It can be understood as dividing the whole number into equal parts and then counting the required number of those parts.
The general process is as follows:
Identify the Parts of the Fraction – The fraction is made up of two parts – a numerator (the top number) and a denominator (the bottom number). The numerator tells you the number of parts you’re looking for, while the denominator tells you into how many equal parts the whole is divided.
Divide the Whole Number – Divide the whole number by the denominator of the fraction. This step gives you the value of each equal part.
Multiply the Result by the Numerator – The result from the previous step is then multiplied by the numerator of the fraction. This tells you the value of the fraction of the whole number you’re looking for.
Let’s break it down with a couple of examples:
Example 1 – What is 1/2 of 20?
Understand the fraction – Here, our fraction is 1/2. The numerator is 1, which means we’re looking for 1 part. The denominator is 2, which means the whole is divided into 2 equal parts.
Divide the whole number – Divide 20 by 2. The result is 10. This means that each part of the whole (when divided into 2 equal parts) is 10.
Multiply the result by the numerator – Multiply 10 by 1. The result is 10. So, 1/2 of 20 is 10.
Example 2 – What is 3/4 of 16?
Understand the fraction – Here, our fraction is 3/4. The numerator is 3, so we’re looking for 3 parts. The denominator is 4, so the whole is divided into 4 equal parts.
Divide the whole number – Divide 16 by 4. The result is 4. This means each part of the whole (when divided into 4 equal parts) is 4.
Multiply the result by the numerator – Multiply 4 by 3. The result is 12. So, 3/4 of 16 is 12.
This method works for any fraction and any whole number. With practice, finding fractions of whole numbers becomes an easy and automatic process, helping you to solve more complex problems.