Equivalent Fractions Worksheets
About These 15 Worksheets
Our equivalent fractions worksheets will help students understand and practice the concept of equivalent fractions. Equivalent fractions are fractions that represent the same value or proportion, even though they may have different numerators and denominators. For example, 1/2 is equivalent to 2/4 and 4/8, because they all represent the same portion of a whole. These worksheets typically include a variety of exercises such as filling in missing numerators or denominators, simplifying fractions, or identifying pairs of equivalent fractions. Through repetitive practice, students reinforce their ability to recognize and generate equivalent fractions, which is a key skill in understanding more advanced math concepts.
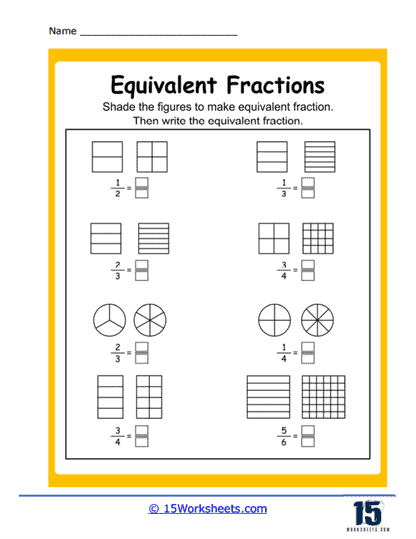
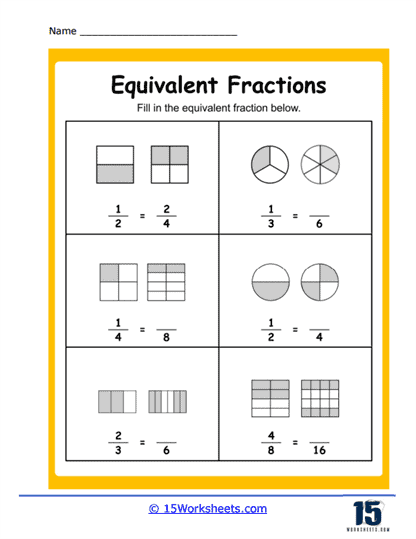
The worksheets often include visual aids, such as fraction bars or pie charts, to help students grasp the idea that different fractions can represent the same part of a whole. These visuals are particularly useful for younger students or those who benefit from seeing the abstract concept in a more concrete form. For older students, equivalent fractions worksheets might incorporate more complex problems, such as comparing and ordering fractions or applying the concept to real-world scenarios, like measuring ingredients in a recipe. These activities build foundational skills that are essential for learning operations with fractions, such as addition, subtraction, and division of fractions.
A Look At The Worksheets
Equivalent fractions are one of those magical math concepts where two things that look completely different turn out to be exactly the same-kind of like Clark Kent and Superman, or your teacher before and after coffee. The worksheets in this collection offer a rich and varied journey into the world of equivalent fractions, using everything from clever visual tricks to missing-number mysteries. They’re designed not just to teach the rules, but to help students feel the equivalence-right in their mathematical bones.
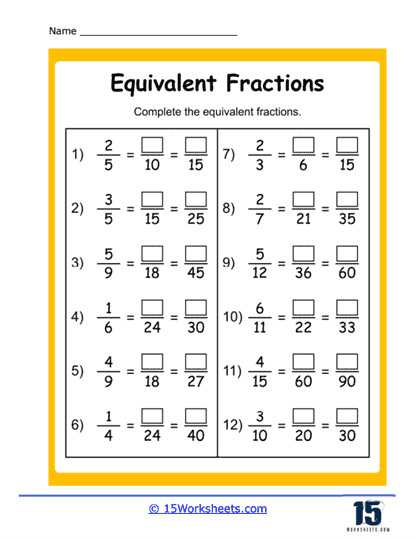
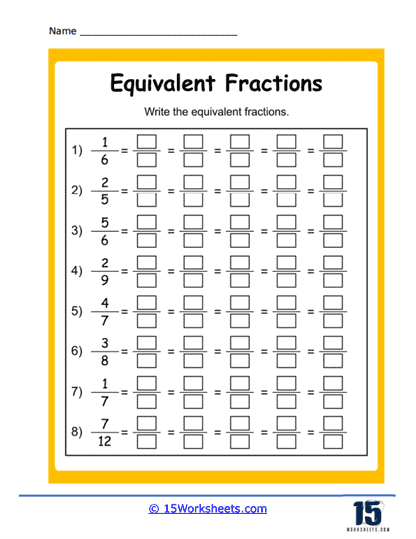
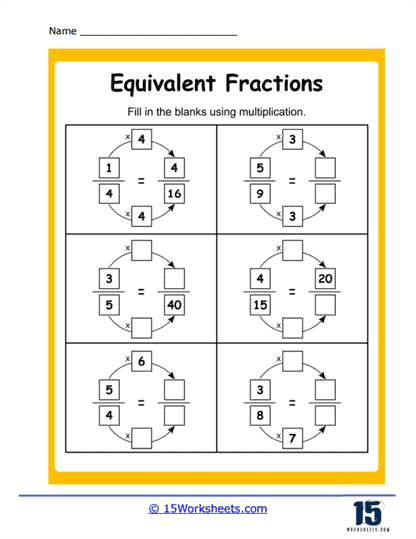
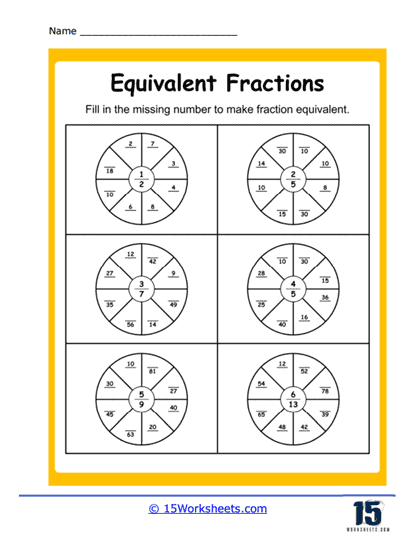
We begin with the classic detective work of missing numbers. In Missing Numerators, students play fraction sleuths, hunting for the absent top half of the fraction that makes the math work. Numerator or Denominator adds a twist: is it the top or bottom that’s gone rogue? Meanwhile, Making 1/2 challenges students to discover just how many different ways you can split a pizza and still call it “half” (hint: a lot). These worksheets lay the foundation for understanding the structure of fractions and how multiplying or dividing both parts by the same number doesn’t change the value-just the outfit it’s wearing.
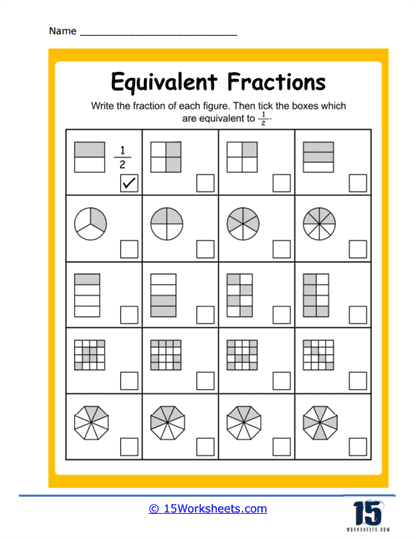
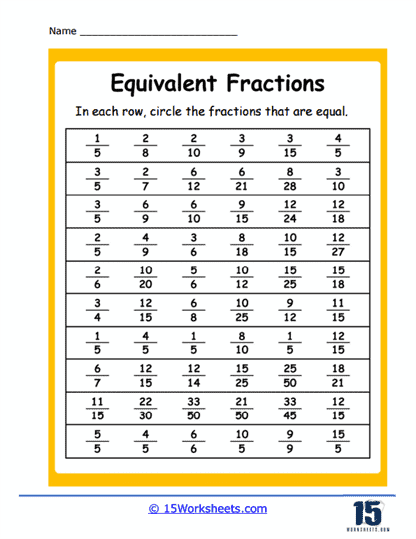
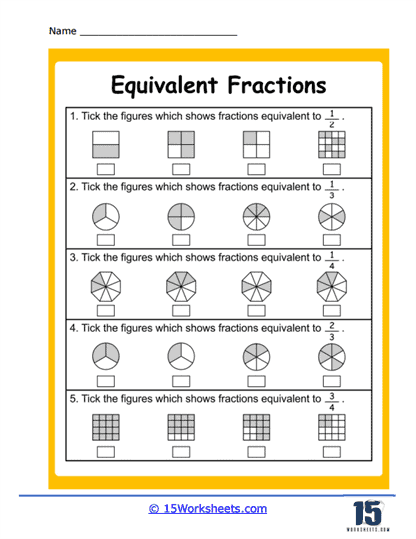
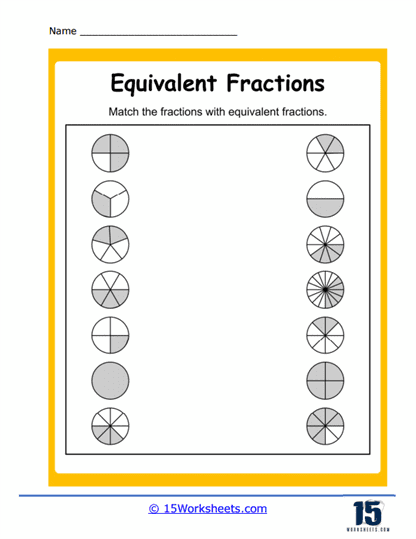
Next comes a buffet of matching activities that help cement visual and numerical relationships. Matching Visuals to Fractions lets students pair fraction names with their pie-chart soulmates. Match Those Values and Equal Values crank up the challenge with numeric comparisons, prompting the all-important question: is 4/6 really just 2/3 in disguise? Spoiler: yes. These exercises make it clear that different numbers can whisper the same truth-especially in Fraction Land, where one slice of logic cuts through multiple forms.
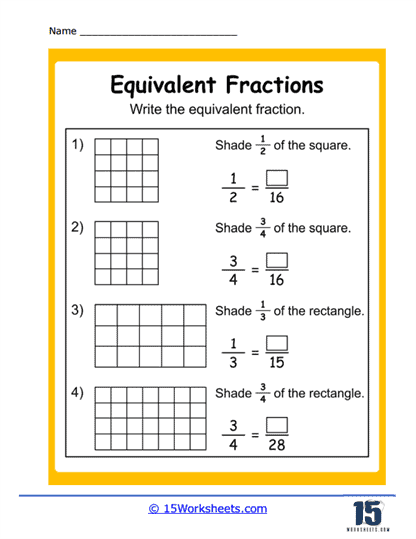
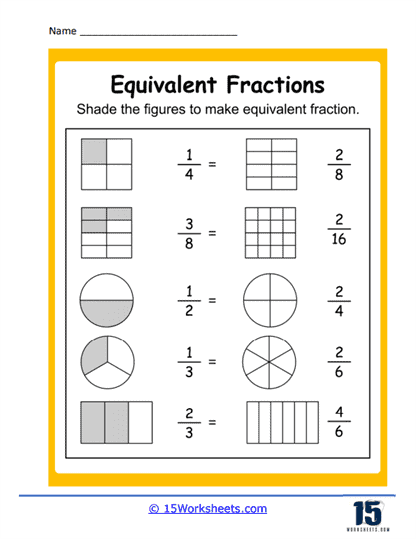
Then, things get artsy. Shading Equivalent Fractions has students grab their imaginary crayons and bring fractions to life through color. The circular-themed trio-Circle Equal Fractions, Matching Circles, and Equivalent Circles-invites learners to explore how different slices of the same pie can represent the same amount, even if they’re cut in wildly different ways. And Equivalent Fraction Wheels adds a dynamic twist, turning the concept into a game-show wheel of fortune where every spin lands on a new equivalent pair. These visual exercises offer a hands-on understanding of what equality looks like, not just what it calculates to.
We get philosophical-or at least logical. Building Left to Right asks students to lay out equivalent fractions like puzzle pieces, creating side-by-side comparisons that reinforce how one form becomes another. What Makes Sense brings the internal voice into play-does this fraction feel right? Is it logical? These worksheets go beyond memorization, asking students to trust their sense of reason, to look at a fraction and just know if it’s telling the truth.
How Do You Identify Equivalent Fractions?
A fraction is considered equivalent to another fraction if they both represent the same quantity or proportion. For instance, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. But how can you tell if two fractions are equivalent? Here are the steps:
Step 1) Understanding the Principle of Equivalent Fractions
To understand equivalent fractions, you should know that when you multiply or divide both the numerator (the top number) and the denominator (the bottom number) of a fraction by the same non-zero number, you get a fraction equivalent to the original.
For example, if you multiply the numerator and the denominator of 1/2 by 2, you get 2/4. Even though 1/2 and 2/4 look different, they represent the same value.
Step 2) Cross-Multiplication
A common method to identify if two fractions are equivalent is by cross-multiplication. This method involves multiplying the numerator of the first fraction by the denominator of the second fraction and comparing that result with the result of multiplying the denominator of the first fraction by the numerator of the second.
For example, are 2/3 and 4/6 equivalent?
By cross-multiplication:
Multiply the numerator of the first fraction (2) by the denominator of the second fraction (6), which equals 12.
Multiply the denominator of the first fraction (3) by the numerator of the second fraction (4), which equals 12.
Since both results are the same (12=12), it shows that the fractions are equivalent.
Step 3) Simplifying Fractions
Another method to identify equivalent fractions is by simplifying one or both fractions to their simplest form. If the fractions are equivalent, they will simplify to the same value.
For example, to check if 3/4 and 6/8 are equivalent:
Simplify 6/8 by dividing both the numerator and denominator by their greatest common divisor (2), you get 3/4.
Since both fractions simplify to 3/4, they are equivalent.
It’s important to note that when identifying equivalent fractions, the key is to understand that fractions are just representations of numbers and that the same number can be represented in many different ways. The same part of a whole can be depicted by different fractions depending on how many pieces you divide the whole into. By recognizing this, you can identify equivalent fractions and make sense of problems involving fractions.