Two Dimensional Shapes Worksheets
About These 15 Worksheets
These worksheets will help students develop a comprehensive understanding of two-dimensional geometric shapes. These worksheets, such as the ones shown above, are designed to be engaging and interactive, encouraging students to explore and recognize various 2D shapes and their properties. Through a variety of exercises and activities, these worksheets aim to build foundational geometry skills that are crucial for more advanced mathematical concepts.
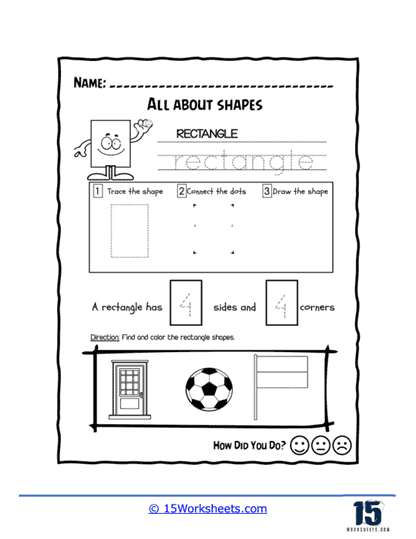
One of the primary goals of 2D Shapes worksheets is to help students identify different shapes. Common shapes featured in these worksheets include circles, squares, triangles, rectangles, hexagons, and sometimes more complex shapes like pentagons and octagons. Worksheets like “Circle Fun” and “Rectangle Roundup” guide students through the process of recognizing these shapes by presenting them in various forms and contexts. For instance, students might trace shapes, connect dots to form shapes, or draw shapes themselves. These activities enhance their ability to distinguish between different shapes and understand their unique characteristics.
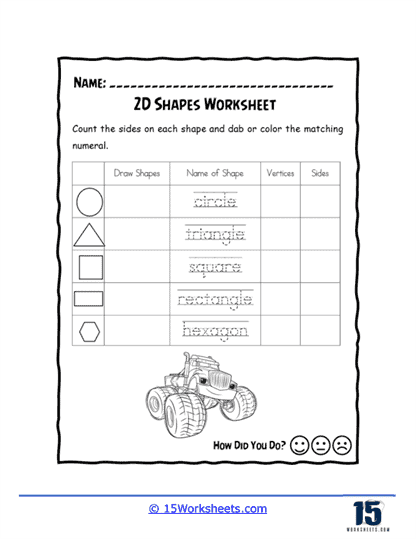
Counting sides and vertices is another key skill explored in 2D Shapes worksheets. Activities often require students to count the number of sides and vertices (corners) of each shape. In worksheets like “Count the Sides,” students are presented with various shapes and asked to identify and count their sides and vertices. This exercise helps students understand the defining properties of each shape. For example, a triangle has three sides and three vertices, while a square has four sides and four vertices. By repeatedly counting and comparing these features, students reinforce their understanding of the basic properties of 2D shapes.
Color-coding and matching exercises are also common in these worksheets. Students might be given a set of shapes and a color code to follow, as seen in “Ice Cream Shapes.” In this activity, students color each shape according to specific instructions, such as coloring circles in yellow and squares in pink. This type of exercise not only makes the learning process enjoyable but also helps students associate shapes with visual cues. The use of colors can aid memory retention and make the learning experience more dynamic.
Sorting and categorizing shapes is another frequent exercise found in 2D Shapes worksheets. For example, in the “Shape Sorters” worksheet, students cut out pictures of various objects and sort them into categories based on their shapes. This hands-on activity helps students practice classifying shapes and reinforces their ability to identify shapes in different contexts. Sorting exercises encourage students to think critically about the properties of shapes and how they can be grouped based on these properties.
Tracing and drawing exercises are fundamental components of these worksheets. Activities like those in “Square Quest” and “Triangle Time” involve students tracing shapes to become familiar with their forms. They might also draw shapes within designated spaces, which helps improve their fine motor skills and reinforces shape recognition. Tracing and drawing provide a tactile learning experience, allowing students to physically engage with the shapes they are studying.
Some worksheets incorporate counting and matching numerals with shapes, such as “How Many Sides?” In these exercises, students count the sides of each shape and then dab or color the numeral that matches the correct number of sides. This type of activity helps students connect their counting skills with geometric concepts, reinforcing their understanding of both numbers and shapes.
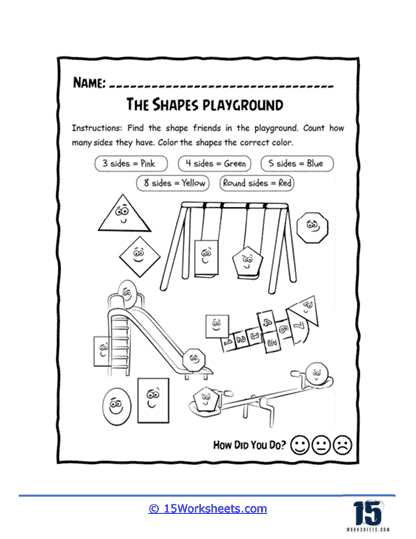
Worksheets like “Shape Playground” integrate playful scenes with geometric learning. In this worksheet, students explore a playground scene filled with various shapes and count the sides of each shape friend. They then color the shapes according to a specific color code based on the number of sides. This engaging approach makes the learning process fun and relatable, helping students see geometry in real-world contexts.
Naming shapes and practicing shape vocabulary is another important aspect of these worksheets. Exercises often include spaces for students to write the names of shapes, as seen in “Shape Count Fun.” Copying the word associated with each shape, such as “circle” or “triangle,” helps reinforce spelling and literacy skills while solidifying the students’ understanding of shape names.
Highlighting shapes within mixed groups is another common exercise. In worksheets like “Highlight All the Circles,” students are asked to find and highlight all instances of a particular shape within a mixed group of various shapes. This activity helps improve visual discrimination and attention to detail as students carefully search for specific shapes among many.
The worksheets also include additional practice problems that combine multiple skills. For instance, in “Shape Detective,” students might be asked to identify, sort, and color shapes, integrating recognition, classification, and coloring skills. These comprehensive exercises ensure that students practice a range of skills within a single worksheet, providing a well-rounded understanding of 2D shapes.
What Are Two Dimensional Shapes?
Two-dimensional (2D) shapes are flat figures that have only two dimensions – length and width. They do not have any thickness or depth, which means they can be drawn on a flat surface like a piece of paper. Here are the most common types of 2D shapes:
Circle – A circle is a round shape where all points on its perimeter are equidistant from a central point, known as the center. This constant distance from the center to any point on the circle is called the radius. Circles are characterized by properties such as diameter (twice the radius) and circumference (the distance around the circle), and they have no edges or vertices.
Square – A square is a four-sided polygon, or quadrilateral, with all sides of equal length and all interior angles measuring 90 degrees. The equal sides and angles make it a regular polygon, and it can also be classified as a special type of rectangle and rhombus. Squares have symmetrical properties and are often used in geometry, tiling, and design due to their regularity and simplicity.
Rectangle – A rectangle is a quadrilateral with four right angles, meaning each angle is 90 degrees. Opposite sides of a rectangle are equal in length, making it a type of parallelogram. Rectangles are commonly seen in everyday objects such as books, screens, and tables, and their area is calculated by multiplying the length by the width.
Triangle – A triangle is a polygon with three sides and three angles, making it the simplest form of polygon. The sum of the interior angles of a triangle always equals 180 degrees. Triangles come in various forms, including equilateral, isosceles, and scalene, and are fundamental in geometry due to their basic yet diverse properties.
a. Equilateral Triangle – An equilateral triangle is a special type of triangle where all three sides are of equal length, and all three internal angles are equal, each measuring 60 degrees. This symmetry gives it unique properties in geometry, making it a regular polygon. Equilateral triangles are often used in constructions and design due to their aesthetic appeal and balance.
b. Isosceles Triangle – An isosceles triangle has two sides of equal length and two equal angles opposite those sides. This symmetry means it has reflective symmetry along the line bisecting the angle between the two equal sides. Isosceles triangles are common in architecture and art because of their balanced proportions and structural stability.
c. Scalene Triangle – A scalene triangle is a type of triangle where all three sides and all three angles are different. This lack of symmetry makes scalene triangles unique and less common than equilateral or isosceles triangles. They demonstrate the diversity of triangle properties and are useful in various mathematical and real-world applications where irregular shapes are involved.
Oval (Ellipse) – An oval, or ellipse, is a stretched circle with two focal points such that the sum of the distances from any point on the ellipse to the two foci is constant. Unlike a circle, an ellipse has two axes: the major axis (longest diameter) and the minor axis (shortest diameter). Ellipses appear in various natural and astronomical contexts, such as the orbits of planets.
Hexagon – A hexagon is a six-sided polygon with six angles. In a regular hexagon, all sides and angles are equal, each internal angle measuring 120 degrees. Hexagons are prominent in nature, such as in the structure of honeycombs, and are efficient shapes for tiling due to their ability to cover a plane without gaps.
Pentagon – A pentagon is a five-sided polygon with five angles. In a regular pentagon, all sides and angles are equal, with each internal angle measuring 108 degrees. Pentagons are found in various contexts, from architecture and art to the structure of certain molecular compounds.
Heptagon – A heptagon is a seven-sided polygon with seven angles. In a regular heptagon, all sides and angles are equal, with each internal angle measuring approximately 128.57 degrees. Heptagons are less common in everyday applications but are studied in geometry for their interesting properties and symmetrical structure.
Octagon – An octagon is an eight-sided polygon with eight angles. In a regular octagon, all sides and angles are equal, with each internal angle measuring 135 degrees. Octagons are commonly seen in stop signs and are used in various design and architectural elements for their balanced shape.
Nonagon – A nonagon is a nine-sided polygon with nine angles. In a regular nonagon, all sides and angles are equal, with each internal angle measuring 140 degrees. Nonagons are less frequently encountered but are studied for their unique properties in polygonal geometry.
Decagon – A decagon is a ten-sided polygon with ten angles. In a regular decagon, all sides and angles are equal, with each internal angle measuring 144 degrees. Decagons are often used in tiling and design for their complex yet symmetrical appearance.
Trapezoid (US) / Trapezium (UK) – A trapezoid (in the US) or trapezium (in the UK) is a four-sided polygon with at least one pair of parallel sides. The parallel sides are called the bases, while the non-parallel sides are the legs. Trapezoids can have various shapes, and their properties are useful in both theoretical geometry and practical applications such as in engineering and design.
Parallelogram – A parallelogram is a four-sided polygon where opposite sides are parallel and equal in length. Opposite angles in a parallelogram are equal, and adjacent angles are supplementary, meaning they add up to 180 degrees. Parallelograms include special types like rectangles, squares, and rhombuses, and are fundamental in the study of geometry and physics.
Rhombus – A rhombus is a type of parallelogram where all four sides are of equal length. The opposite angles of a rhombus are equal, and the diagonals bisect each other at right angles, providing symmetrical properties. Rhombuses are often referred to as diamond shapes and appear in various contexts from tiling patterns to the study of crystal structures.
Real World Uses
2D shapes play a fundamental role in our everyday lives, appearing in a wide range of real-world contexts that students regularly encounter. Understanding and recognizing these shapes are essential skills that help students make sense of the world around them. From the moment we wake up, we are surrounded by 2D shapes. For example, the rectangular shape of a smartphone, the circular face of a clock, and the square tiles on a bathroom floor are all practical applications of 2D shapes. These shapes are not only prevalent in objects but also in signs, patterns, and designs we see daily.
In the context of education, 2D shapes are integral to the study of geometry, which lays the groundwork for understanding more complex mathematical concepts. Students might come across 2D shapes in various subjects beyond mathematics, such as art, where they learn to draw and appreciate the aesthetic value of geometric patterns, and in science, where diagrams often involve the use of basic shapes to represent different elements. Recognizing and understanding 2D shapes help students develop spatial awareness and logical reasoning skills, which are critical for problem-solving and analytical thinking.
In the real world, 2D shapes are used extensively in design and architecture. Architects and engineers use geometric shapes to create blueprints and plans for buildings and structures. Understanding the properties of shapes like rectangles, squares, and triangles helps in designing stable and aesthetically pleasing constructions. Interior designers also use these shapes to plan the layout of spaces, ensuring functionality and visual appeal. By learning about 2D shapes, students gain insight into how spaces are organized and how different shapes can be used to create efficient and beautiful designs.
Graphic design and digital media are other fields where 2D shapes are crucial. Designers use software tools to create logos, advertisements, and website layouts, relying heavily on geometric shapes to create visually appealing and effective designs. For instance, circles are often used in logos to convey unity and completeness, while rectangles and squares can represent stability and professionalism. Students interested in these fields can benefit greatly from understanding the principles of 2D shapes and how they can be manipulated to achieve desired visual effects.
In everyday activities, students encounter 2D shapes in games and sports. The rectangular shape of a soccer field, the circular shape of a basketball hoop, and the triangular shape of a billiard rack are all examples of how geometric shapes are integrated into sports and recreational activities. Recognizing these shapes helps students understand the rules and strategies of different games, enhancing their participation and enjoyment.