Three Dimensional Shapes Worksheets
About These 15 Worksheets
These worksheets were developed to help students understand and analyze the properties of three-dimensional geometric shapes. These worksheets introduce and reinforce concepts related to 3D shapes, such as cubes, spheres, cones, cylinders, pyramids, and prisms. Students learn to recognize these shapes, understand their properties, and differentiate them from two-dimensional shapes. The activities on these worksheets range from identifying and naming shapes to more complex tasks like calculating volume and surface area.
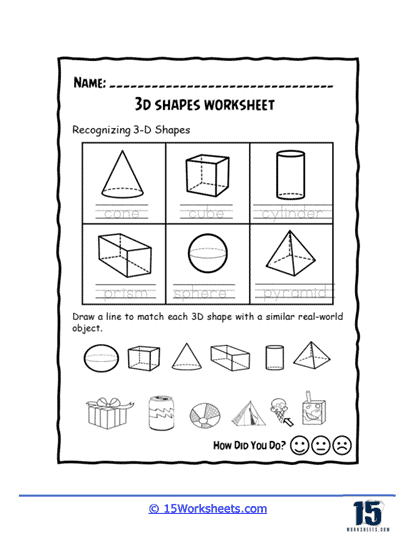
One of the primary skills explored in 3D Shapes worksheets is the identification and naming of shapes. Students are often presented with various 3D shapes and asked to name them. This activity helps students become familiar with the shapes and their names, which is foundational for more advanced geometry. Recognizing a cube, for instance, involves understanding that it has six square faces, twelve edges, and eight vertices. Similar exercises apply to other shapes like spheres, cones, and pyramids.
Another common exercise is comparing and contrasting 2D and 3D shapes. Worksheets might display a 2D shape next to its 3D counterpart, such as a square next to a cube or a circle next to a sphere. Students learn to differentiate between the two, understanding that while a square is flat with two dimensions, a cube is a solid shape with three dimensions. This comparison helps solidify the concept of dimensions and provides a clear visual distinction between flat and solid shapes.
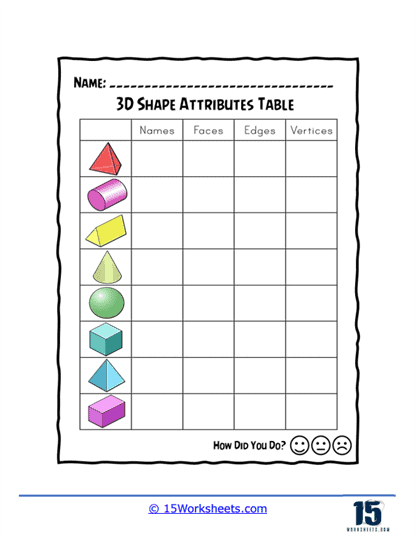
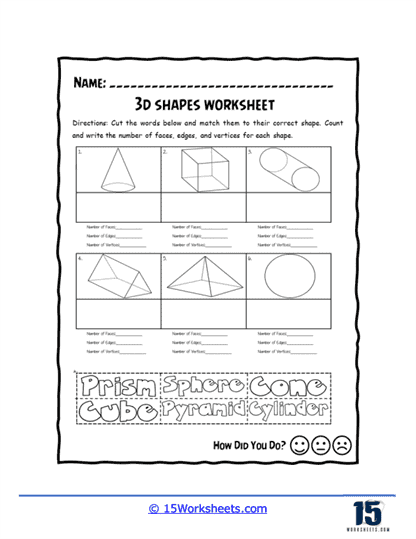
Counting faces, edges, and vertices is a frequent activity on 3D Shapes worksheets. Students are often tasked with counting and recording the number of faces, edges, and vertices on various shapes. For example, they might count that a cube has six faces, twelve edges, and eight vertices, or that a triangular prism has five faces, nine edges, and six vertices. This exercise reinforces their understanding of the structure and components of each shape and helps develop their spatial awareness.
Drawing and constructing 3D shapes is another important aspect of these worksheets. Students might be asked to draw 3D shapes from different perspectives or construct them using nets. A net is a two-dimensional representation that can be folded to form a 3D shape. For example, a net for a cube consists of six connected squares that, when folded, create the cube. This activity helps students visualize how 2D shapes can form 3D objects and improves their spatial reasoning skills.
Calculating volume and surface area is a key component of 3D Shapes worksheets, especially for older students. Worksheets often provide formulas for calculating the volume and surface area of various shapes and then present problems for students to solve. For instance, students might use the formula for the volume of a cube (V = side^3) to calculate the volume of a cube with a side length of 4 units. Similarly, they might use the surface area formula for a cylinder (SA = 2πr^2 + 2πrh) to find the surface area of a cylinder with a radius of 3 units and a height of 5 units. These calculations help students understand the practical applications of geometry and develop their problem-solving skills.
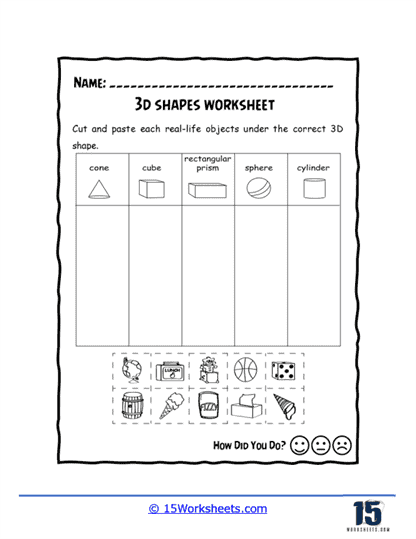
Sorting and classifying 3D shapes is another common exercise. Students might be given a list of shapes and asked to sort them into categories based on specific criteria, such as the number of faces or the type of faces. For example, they might sort shapes into groups with all faces being squares (like cubes) and those with different types of faces (like pyramids). This activity encourages critical thinking and helps students understand the relationships between different shapes.
Matching activities are also popular on 3D Shapes worksheets. Students might be asked to match shapes to their names, descriptions, or nets. For instance, they might match a picture of a cone to the word “cone” or match a net to the 3D shape it forms. Matching activities reinforce students’ recognition skills and help them connect visual representations with their corresponding names and properties.
Real-world applications of 3D shapes are often included to help students understand the relevance of geometry in everyday life. Worksheets might present problems involving objects like cans, boxes, or balls and ask students to identify the shapes and calculate properties like volume or surface area. For example, a worksheet might show a soda can and ask students to calculate its volume, given its height and radius. This helps students see how geometry is used in packaging, construction, and various other fields.
Pattern recognition and tessellation are explored in some 3D Shapes worksheets. Students might be asked to identify patterns in a series of shapes or to understand how shapes fit together to form tessellations. For example, they might explore how cubes can be stacked to fill a space or how different shapes can combine to create a repeating pattern. These activities develop students’ understanding of spatial relationships and symmetry.
Symmetry and transformations are also key concepts in 3D Shapes worksheets. Students might explore how shapes can be rotated, reflected, or translated in three-dimensional space. Worksheets might present problems where students need to visualize and describe the effects of these transformations on 3D shapes. For instance, they might be asked to describe how a pyramid looks when rotated or to identify the axis of symmetry in a given shape.
Understanding and interpreting three-dimensional coordinates is another advanced skill covered in some worksheets. Students might be introduced to the three-dimensional coordinate system and asked to plot points or shapes in three-dimensional space. This involves understanding the x, y, and z axes and how they relate to the positioning of objects. For example, a worksheet might present a problem where students plot the coordinates of a cube’s vertices in a 3D grid.
Worksheets also include puzzles and games related to 3D shapes. For example, students might solve crosswords or word searches with shape-related vocabulary or engage in games where they identify shapes based on clues. These activities make learning fun and help reinforce concepts in an enjoyable way.
Our 3D Shapes worksheets cover a wide range of geometry-related skills. They help students recognize, understand, and analyze three-dimensional shapes through a variety of engaging and interactive activities. By working with these worksheets, students develop essential skills such as spatial reasoning, critical thinking, problem-solving, and the practical application of geometric concepts. Through identifying shapes, counting their components, drawing and constructing shapes, calculating volume and surface area, sorting and classifying, matching, exploring real-world applications, recognizing patterns, understanding transformations, interpreting coordinates, and using technology, students gain a deep and thorough understanding of 3D shapes and their properties.
What Are Three Dimensional Shapes?
Three-dimensional (3D) shapes, also known as solids, have three dimensions: length, width, and height (or depth). These shapes occupy space and have volume, unlike two-dimensional shapes, which only have area. Here are the most common types of 3D shapes:
Cube – A cube is a three-dimensional solid with six equal square faces, twelve equal edges, and eight vertices. Each face meets another face at a right angle, and the angles between the edges are all 90 degrees. Cubes are highly symmetrical and are often seen in dice, ice cubes, and various geometric studies.
Cuboid (Rectangular Prism) – A cuboid, or rectangular prism, is a three-dimensional solid with six rectangular faces, where opposite faces are equal and parallel. It has twelve edges and eight vertices, and all angles between the faces are right angles. Common examples of cuboids include bricks, books, and boxes, and they are essential in understanding volume and surface area in geometry.
Sphere – A sphere is a perfectly round three-dimensional solid where every point on the surface is equidistant from the center. It has no edges or vertices, and its surface is continuous and smooth. Spheres are found in various natural and man-made objects, such as balls, planets, and bubbles, and are used to study properties like volume and surface area in mathematics.
Cylinder – A cylinder is a three-dimensional solid with two parallel circular bases connected by a curved surface. The distance between the bases is the height of the cylinder, and the line segment joining the centers of the bases is the axis. Cylinders are commonly seen in everyday objects like cans, pipes, and barrels, and are fundamental in studying volumes and surface areas of solids.
Cone – A cone is a three-dimensional solid with a circular base and a single vertex, tapering smoothly from the base to the vertex. The height of the cone is the perpendicular distance from the base to the vertex, and the slant height is the distance along the curved surface. Cones are seen in ice cream cones, traffic cones, and are significant in studying volumes and surface areas in geometry.
Pyramid – A pyramid is a three-dimensional solid with a polygonal base and triangular faces that meet at a single point called the apex or vertex. The number of triangular faces corresponds to the number of sides of the base polygon. Pyramids, like the Great Pyramid of Giza, have historical and architectural significance and are used to study geometric properties of solids.
Triangular Pyramid (Tetrahedron) – A triangular pyramid, or tetrahedron, is a pyramid with a triangular base and four triangular faces. It has six edges and four vertices, making it the simplest form of a pyramid. Tetrahedrons are important in molecular chemistry and are used in the study of polyhedral shapes.
Square Pyramid – A square pyramid is a pyramid with a square base and four triangular faces that converge at a single vertex. It has five faces, eight edges, and five vertices. Square pyramids are often seen in architecture and design, such as in ancient Egyptian pyramids, and are studied for their geometric properties.
Prism – A prism is a three-dimensional solid with two parallel, congruent bases connected by rectangular faces. The shape of the bases determines the type of prism, and the height is the perpendicular distance between the bases. Prisms are used in optics to study light refraction and in geometry to explore properties of solids.
Triangular Prism – A triangular prism is a type of prism with triangular bases and three rectangular faces connecting the corresponding sides of the bases. It has five faces, nine edges, and six vertices. Triangular prisms are seen in various applications, such as in structural engineering and the study of light dispersion in optics.
Pentagonal Prism – A pentagonal prism is a type of prism with pentagonal bases and five rectangular faces connecting the corresponding sides of the bases. It has seven faces, fifteen edges, and ten vertices. Pentagonal prisms are used in architecture and geometric studies for their unique properties and structure.
Torus – A torus is a three-dimensional donut-shaped solid with a circular hole in the middle. It is generated by rotating a circle around an axis that is in the same plane as the circle but does not intersect it. Tori are found in various natural and man-made objects, such as inner tubes and lifebuoys, and are significant in the study of topology and geometry.
Ellipsoid – An ellipsoid is a three-dimensional elongated sphere-like shape, where all plane cross-sections are ellipses or circles. It has three axes of different lengths: major, minor, and intermediate. Ellipsoids are used in various scientific fields, including astronomy to model the shape of planets and in engineering to study stress distribution.
Octahedron – An octahedron is a three-dimensional solid with eight equilateral triangular faces, twelve edges, and six vertices. It is one of the five Platonic solids and is highly symmetrical. Octahedrons are found in crystal structures, such as diamonds, and are studied for their geometric and symmetrical properties.
Dodecahedron – A dodecahedron is a three-dimensional solid with twelve pentagonal faces, thirty edges, and twenty vertices. It is another of the five Platonic solids and has significant symmetrical properties. Dodecahedrons are seen in various applications, including dice, and are studied in geometry and mathematical theory.
Icosahedron – An icosahedron is a three-dimensional solid with twenty equilateral triangular faces, thirty edges, and twelve vertices. It is the most complex of the five Platonic solids and is highly symmetrical. Icosahedrons are found in natural structures, such as certain viruses, and are used in geometric studies and in the design of complex shapes.
Why are Three Dimensional Shapes Important?
Three-dimensional (3D) shapes play a fundamental role in our daily lives, often without us even realizing it. From the moment we wake up, we interact with a myriad of 3D objects. Our homes, for instance, are built using principles of three-dimensional geometry, ensuring stability and functionality. The walls, floors, and ceilings form cuboids, while elements like roofs and staircases often incorporate more complex shapes like pyramids and cylinders. Understanding these shapes helps architects and builders design safe and aesthetically pleasing structures, impacting our comfort and safety directly.
In the realm of transportation, 3D shapes are crucial. Cars, buses, bicycles, and airplanes are all meticulously designed using principles of three-dimensional geometry. The aerodynamics of a car, for instance, relies on understanding and optimizing shapes to reduce air resistance and improve fuel efficiency. For the common person, this translates to smoother, safer, and more efficient travel. The seats we sit on, the wheels that move us, and even the storage compartments are all carefully shaped to maximize utility and comfort.
In our households, everyday objects such as furniture, appliances, and gadgets are all designed with three-dimensional considerations. The ergonomic design of a chair, the compact shape of a smartphone, and the efficient layout of a refrigerator’s shelves all rely on an understanding of 3D shapes. These designs make our lives easier, more comfortable, and more productive. For instance, the cylindrical shape of a drinking glass fits well in our hands and holds liquids efficiently, while the rectangular shape of a book makes it easy to store and read.
Advancements in technology have brought three-dimensional shapes to the forefront of innovation. 3D modeling and printing have revolutionized how products are designed and manufactured. This technology allows for rapid prototyping and customization, meaning everyday people can now design and create bespoke items that perfectly fit their needs. Whether it’s a custom phone case, a unique piece of jewelry, or even prosthetic limbs, 3D printing makes personalization accessible and affordable.
In medicine, the importance of three-dimensional shapes cannot be overstated. Imaging technologies like CT scans and MRIs provide detailed 3D representations of the human body, allowing doctors to diagnose and treat conditions with greater precision. This means better healthcare outcomes for patients, as doctors can see exactly what’s happening inside the body and plan surgeries or treatments more effectively. For the common person, this translates to more accurate diagnoses, less invasive procedures, and faster recoveries.