Points, Lines, and Planes Worksheets
About These 15 Worksheets
These worksheets were designed to introduce and reinforce fundamental geometric concepts. These worksheets are integral to early mathematics education, providing students with a solid foundation in geometry. Through various exercises and problems, students learn to identify, classify, and describe the basic elements of geometry: points, lines, and planes. These worksheets are typically used in elementary and middle school settings, where they serve as both teaching tools and assessment instruments.
Benefits of These Worksheets
They can help students develop spatial awareness by encouraging them to visualize and comprehend geometric shapes and structures. This skill is crucial not only in mathematics but also in fields such as engineering, architecture, and art. These worksheets promote critical thinking and problem-solving abilities. Students must analyze figures, identify relationships between different geometric elements, and apply logical reasoning to classify and describe them. Working on these worksheets enhances students’ precision and attention to detail. Geometry requires accurate representation and naming of figures, which cultivates meticulousness and accuracy in students’ work. Lastly, these worksheets provide a structured and systematic way to learn geometry, allowing students to progress from simple to complex concepts at a manageable pace.
Math Skills Explored
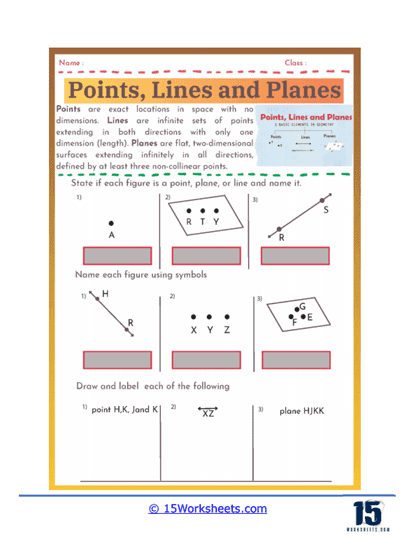
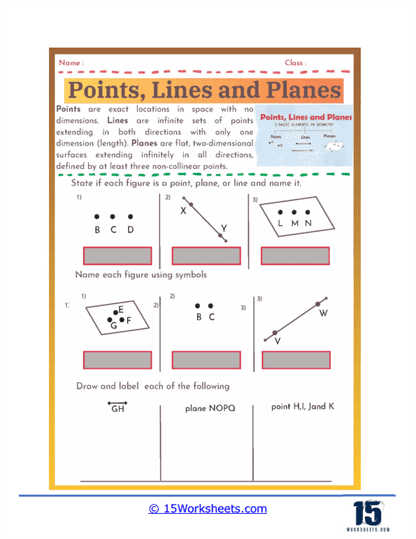
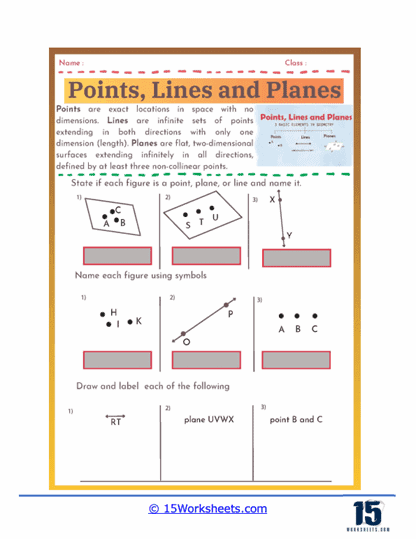
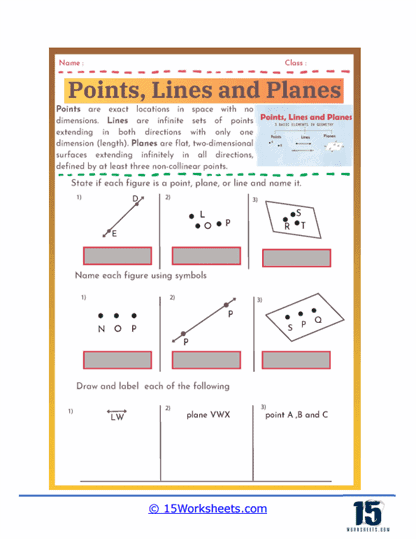
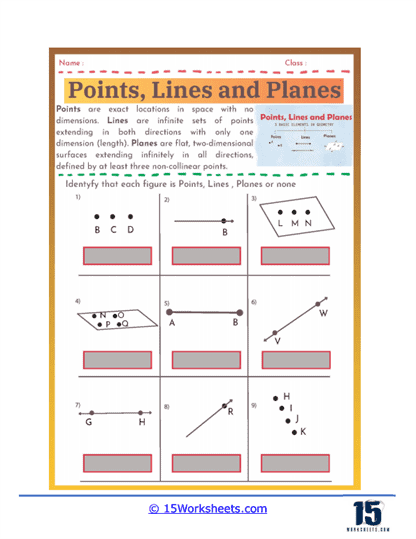
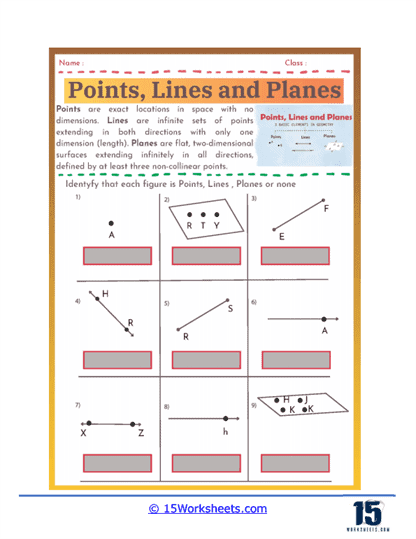
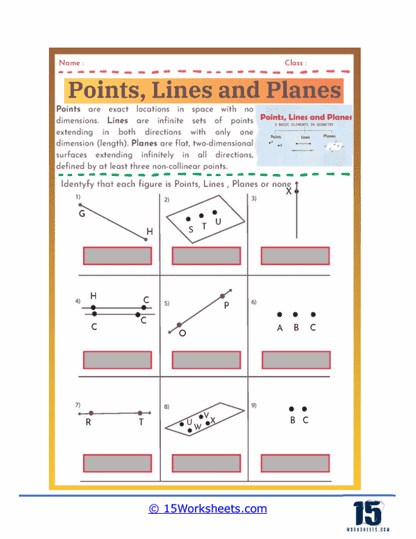
Understanding Basic Geometric Terms – Points, lines, and planes worksheets review the fundamental geometric terms and concepts that are the building blocks of geometry. Students learn to identify and define a point as an exact location in space with no size, a line as a straight path extending infinitely in both directions, and a plane as a flat surface that extends infinitely in all directions. This foundational knowledge is crucial for understanding more complex geometric concepts and is reinforced through various exercises that require precise definitions and visual identification.
Plotting and Identifying Points – Students practice plotting and identifying points on a coordinate plane, which is essential for understanding spatial relationships. Worksheets often include problems where students must locate points using coordinates, reinforcing their ability to navigate the Cartesian coordinate system. This skill is fundamental for graphing functions, analyzing geometric shapes, and solving problems involving distance and midpoints.
Understanding Line Relationships – Worksheets on points, lines, and planes help students understand different types of line relationships, such as parallel, perpendicular, and intersecting lines. Students learn to recognize and classify these relationships based on given diagrams or coordinate pairs. This understanding is important for solving problems related to angles, slopes, and geometric constructions, and it lays the groundwork for studying more advanced geometric relationships and theorems.
Working with Planes – Students explore the concept of planes and their properties, including how lines and points can lie on the same plane or in different planes. Worksheets often include problems that require students to visualize and draw planes and to understand how lines and points interact within and across planes. This spatial reasoning skill is vital for three-dimensional geometry, which is used in fields such as architecture, engineering, and computer graphics.
Measuring and Constructing – Measuring and constructing geometric figures are key skills reviewed in these worksheets. Students practice using rulers, protractors, and compasses to accurately measure distances, angles, and to construct points, lines, and planes. These activities develop their precision and attention to detail, which are important for both theoretical geometry and practical applications in various technical fields.
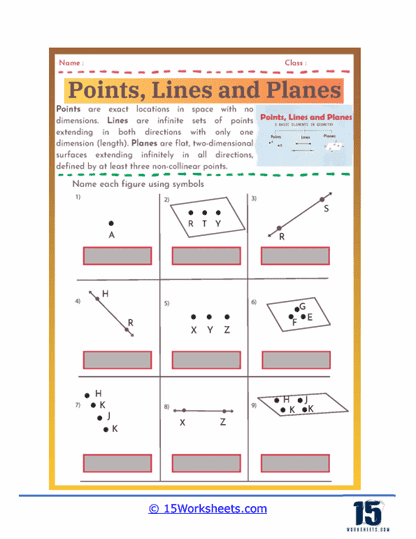
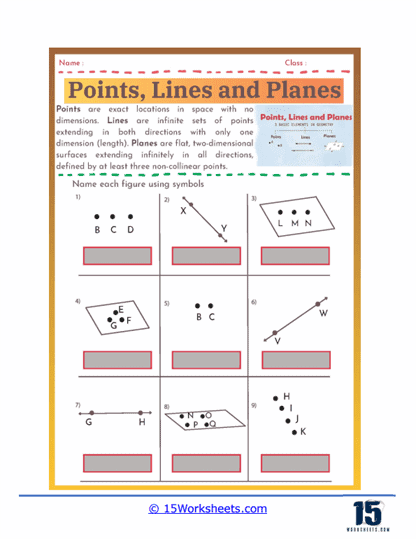
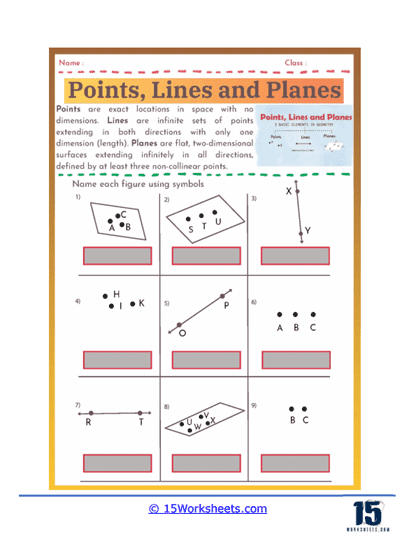
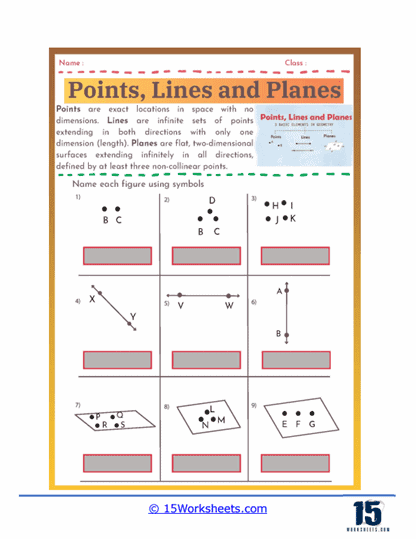
Applying Geometric Notation – Proper use of geometric notation is emphasized in points, lines, and planes worksheets. Students learn to use symbols to represent points (e.g., point A), lines, and planes (e.g., plane ABC). This skill is essential for clear communication in geometry and for writing and understanding geometric proofs and solutions.
Solving Real-World Problems – Worksheets often include real-world problems that require applying the concepts of points, lines, and planes. Students might solve problems related to navigation, construction, or design, where understanding the relationships and properties of these geometric elements is crucial. These problems help students see the practical relevance of geometry in everyday life and various professional contexts.
Types of Exercises
Points, lines, and planes worksheets typically include a variety of exercises and practice problems to reinforce these skills. Some common types of exercises are:
Identification Exercises– These exercises present students with geometric figures and ask them to identify whether the figures are points, lines, line segments, rays, or planes. For example, a worksheet might show a figure with three labeled points and ask students to identify and name a line passing through two of the points.
Classification Problems – In these problems, students classify geometric figures based on their properties. For instance, a worksheet might include several pairs of lines and ask students to classify each pair as parallel, perpendicular, or intersecting.
Drawing and Labeling Exercises – These exercises require students to draw geometric figures based on given descriptions and label them using appropriate geometric symbols. For example, a worksheet might ask students to draw a line segment connecting two points and label it.
Naming Figures – Students practice using geometric symbols to name figures. They might be given a figure with several points labeled and asked to name all the possible lines, line segments, and rays that can be formed.
Geometric Relationships – These problems explore the relationships between different geometric elements. For example, students might be asked to determine whether two lines are parallel, perpendicular, or intersecting based on their positions in a plane.
Real-World Applications – Some worksheets include problems that apply geometric concepts to real-world situations. For instance, students might be asked to identify parallel and perpendicular lines in a diagram of a city map.
Real World Examples
Architecture and Construction
In architecture and construction, the concepts of points, lines, and planes are fundamental. Architects use points to specify exact locations for structural elements and features within their designs. Lines represent edges, beams, and structural components, while planes are used to design and analyze walls, floors, and ceilings. These geometric concepts help ensure that buildings are designed accurately and constructed safely. For instance, architects and engineers must determine the correct alignment and angles between structural components to ensure stability and aesthetic appeal.
Consider the layout of a city with a grid of streets and avenues. Each intersection of a street and an avenue represents a point, each street and avenue represents a line, and the entire grid represents a plane. A points, lines, and planes worksheet might present a simplified version of this map and ask students to identify various geometric elements. For example, a problem might show a map with labeled streets and avenues and ask students to identify all the intersections (points), name the streets and avenues using geometric symbols (lines), and determine whether certain streets and avenues are parallel or perpendicular.
Engineering
Engineers regularly apply the concepts of points, lines, and planes in their work. In mechanical engineering, for example, the design of machinery involves understanding how different parts will align and interact in three-dimensional space. Points can represent specific locations for drilling holes or placing components, lines can indicate the paths of moving parts or electrical connections, and planes can represent surfaces where components must fit together precisely. These geometric considerations are essential for creating functional, efficient, and safe mechanical systems.
Navigation and GPS
Navigation and GPS technology rely heavily on geometric concepts. Points are used to represent specific locations on maps, such as destinations or waypoints. Lines indicate routes or paths between these points, and planes can represent the Earth’s surface or various layers of a mapping system. By understanding and utilizing these concepts, navigational systems can provide accurate directions and optimize travel routes, whether for driving, flying, or sailing.
Computer Graphics and Game Design
In computer graphics and game design, points, lines, and planes are crucial for creating realistic and interactive virtual environments. Points are used to define vertices in 3D models, lines form the edges between these vertices, and planes create surfaces of objects. Understanding these concepts allows designers to build complex shapes, animate objects, and simulate realistic movements and interactions in virtual worlds. These geometric principles are essential for producing visually appealing and immersive digital experiences.
Robotics and Automation
Robotics and automation also utilize the concepts of points, lines, and planes. In robotic movement and manipulation, points can define target locations for the robot to move to or interact with. Lines can represent paths or trajectories that the robot must follow, and planes can help determine the workspaces or operational areas where the robot performs tasks. Precise geometric calculations ensure that robots operate efficiently, accurately, and safely in manufacturing, medical procedures, and other applications.
Art and Design
Artists and designers use points, lines, and planes to create compositions, sculptures, and various artworks. Points can represent specific locations for elements within a piece, lines can define shapes, forms, and structures, and planes can establish surfaces and areas of interest. Understanding these concepts allows artists to create balanced and visually appealing works. In design, these principles help in creating products, spaces, and visual communications that are both functional and aesthetically pleasing.
Surveying and Cartography
Surveyors and cartographers use geometric principles to measure and map the Earth’s surface. Points represent specific locations such as landmarks or survey markers, lines indicate boundaries, roads, and pathways, and planes can represent larger geographic areas or layers within a map. These geometric concepts are essential for creating accurate maps and property boundaries, which are crucial for land development, urban planning, and environmental management.
Physics and Astronomy
In physics and astronomy, points, lines, and planes are used to model and understand spatial relationships and movements. Points can represent locations of particles, stars, or planets, lines can indicate paths of motion or light rays, and planes can represent orbital paths or reference frames. These concepts help scientists and researchers understand the structure of the universe, the behavior of physical systems, and the relationships between celestial bodies.