Geometry Worksheets
Related Worksheets
About These Worksheets
Geometry worksheets are essential educational resources designed to help students understand, practice, and master various geometric concepts. They provide structured opportunities for learners to engage with geometric principles through a variety of problems and exercises. These worksheets can be tailored to different educational levels, from elementary to high school and beyond, ensuring that the content matches the students’ proficiency and curriculum standards.
What is Geometry?
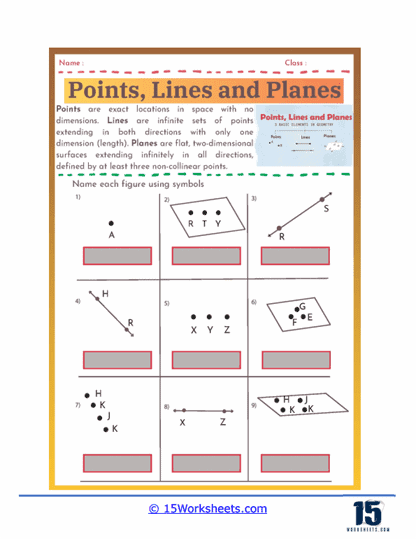
Geometry is a branch of mathematics that deals with the properties, relationships, and measurements of points, lines, angles, surfaces, and solids. It is one of the oldest fields of study in mathematics, with origins dating back to ancient civilizations such as the Egyptians, Babylonians, and Greeks. The term “geometry” comes from the Greek words “geo,” meaning earth, and “metron,” meaning measure, reflecting its historical role in surveying land and understanding spatial relationships.
Geometry is profoundly embedded in various facets of the modern world, playing a critical role in fields like architecture, engineering, and computer science. In architecture, geometric principles guide the design and construction of buildings and structures, ensuring aesthetic appeal, stability, and functionality. Architects use geometry to create detailed blueprints and plans that translate abstract concepts into tangible forms, considering angles, symmetry, and spatial relationships to maximize space efficiency and structural integrity. Similarly, in engineering, geometry is essential for designing and analyzing components and systems. Engineers rely on geometric calculations to determine the dimensions, shapes, and tolerances necessary for machinery, vehicles, and infrastructure, ensuring that each part fits and functions correctly within the larger system.
Beyond physical structures, geometry is indispensable in the digital realm, particularly in computer graphics, robotics, and geographic information systems (GIS). In computer graphics, geometric algorithms generate and manipulate visual images, enabling the creation of realistic 3D models, animations, and virtual environments used in video games, simulations, and films. Robotics employs geometric principles to navigate and interact with physical spaces, allowing robots to perform tasks with precision and efficiency. In GIS, geometry helps in mapping and analyzing spatial data, facilitating urban planning, environmental monitoring, and navigation systems. These applications highlight how geometry underpins technological advancements and contributes to solving complex problems in our increasingly interconnected world.
Types of Problems
Geometry worksheets encompass a wide range of topics, each addressing different geometric principles. These can be broadly categorized to help students systematically learn and apply various aspects of geometry.
Basic Shapes and Properties – One fundamental type of problem in geometry worksheets involves identifying and naming basic geometric shapes. Students might be asked to recognize and label circles, squares, triangles, rectangles, and polygons. This foundational knowledge sets the stage for more complex geometric tasks. Additionally, exercises focused on the properties of these shapes delve into their defining characteristics, such as the number of sides, vertices, and angles. Understanding these properties is crucial for students to progress in their geometric studies.
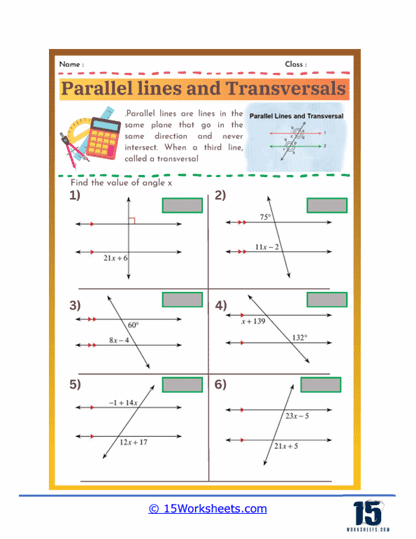
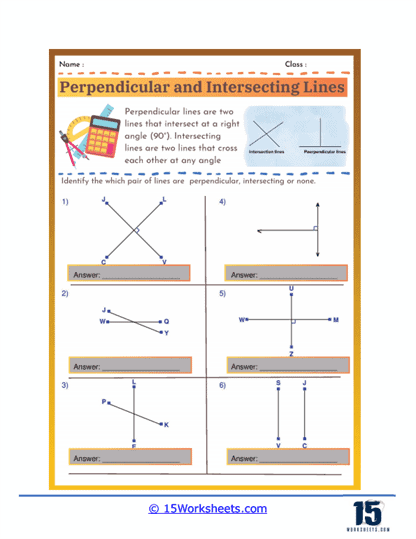
Angles – Worksheets addressing angles help students become familiar with the different types of angles and their properties. Problems might require students to identify and classify angles as acute, obtuse, right, or straight, sharpening their ability to distinguish between these fundamental geometric elements. Measuring angles with a protractor is another common exercise, teaching practical skills for precision. Furthermore, problems involving angle relationships-such as complementary, supplementary, and vertical angles-along with angles formed by parallel lines cut by a transversal, help students understand how angles interact in various configurations.
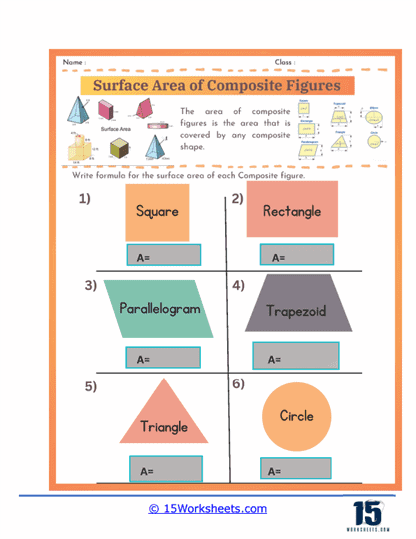
Perimeter, Area, and Volume – Calculating perimeter, area, and volume is a key aspect of geometry that has practical applications in numerous fields. Perimeter exercises involve finding the total length around various shapes, both regular and irregular. Area problems require students to compute the space within basic shapes like squares, rectangles, triangles, and circles, as well as more complex figures such as trapezoids and parallelograms. For three-dimensional shapes, worksheets might include calculating surface area and volume, helping students understand the extent and capacity of objects like cubes, cylinders, spheres, and prisms.
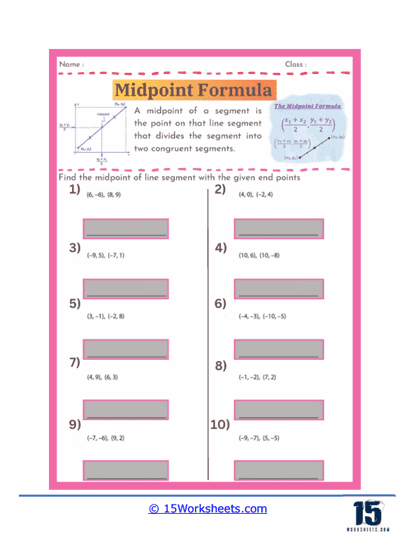
Coordinate Geometry – Coordinate geometry introduces students to the Cartesian plane and the concept of plotting points. Simple problems might involve placing points on a coordinate grid, while more advanced exercises include graphing lines and shapes based on given equations or coordinates. Distance and midpoint problems help students develop skills in calculating the distance between two points and finding the center point of a line segment. These tasks are foundational for higher-level mathematics and practical applications in various fields, including engineering and computer science.
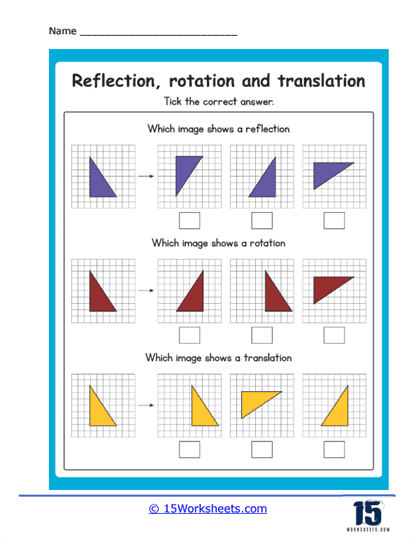
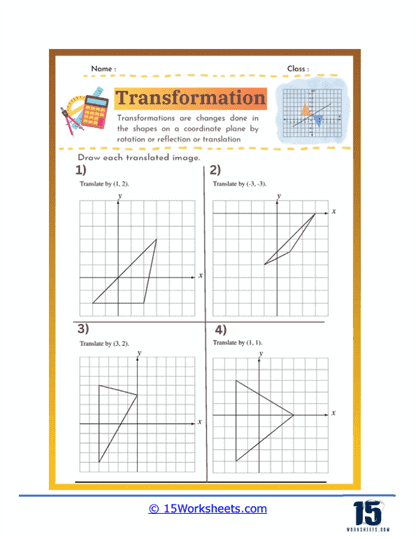
Transformations – Transformations are a significant area in geometry that involves moving shapes within the coordinate plane. Worksheets might include problems on translations, which shift shapes without altering their size or orientation. Rotations involve turning shapes around a fixed point, requiring students to understand angles and rotational symmetry. Reflections focus on flipping shapes over a line, while dilations involve resizing shapes proportionally. These exercises help students understand how shapes can change position and size while maintaining their essential properties.
Congruence and Similarity – Problems related to congruence and similarity help students understand the relationships between shapes. Identifying congruent shapes involves recognizing figures that are identical in shape and size. Proving congruence through postulates and theorems (such as SSS, SAS, ASA, AAS) deepens students’ understanding of geometric proofs. Similarity problems require students to identify shapes that are the same in form but different in size, often using proportions to solve for missing lengths. These concepts are critical for higher-level geometry and real-world applications.
Triangles – Triangles are a fundamental shape in geometry, and worksheets often include problems on classifying triangles based on their sides (equilateral, isosceles, scalene) and angles (acute, obtuse, right). The triangle inequality theorem, which determines if given lengths can form a triangle, is another key concept. Problems applying the Pythagorean theorem help students find missing sides in right triangles, a critical skill for various applications. Special right triangles, such as 30-60-90 and 45-45-90 triangles, are also a focus, with exercises designed to reinforce these specific geometric properties.
Circles – Understanding circles is essential in geometry, and worksheets often include problems identifying parts of a circle such as the radius, diameter, chord, arc, and sector. Calculating the circumference and area of circles is a common exercise, teaching students practical measurement skills. Problems involving arc lengths and sector areas extend this understanding, requiring more complex calculations and a deeper comprehension of circular geometry.
Geometric Constructions – Geometric constructions involve creating precise figures using a compass and straightedge, a skill that is both foundational and practical. Worksheets guide students through constructing geometric figures, such as bisectors and perpendicular lines, fostering a hands-on understanding of geometric principles. These basic constructions are essential for developing spatial reasoning and geometric intuition.
Logical Reasoning and Proofs – Logical reasoning and proofs are at the heart of geometry, developing students’ critical thinking and problem-solving skills. Basic proofs introduce students to the structure and format of geometric arguments, including two-column proofs that logically deduce properties from given information. Problems that involve applying geometric theorems and postulates to prove statements about shapes and their properties deepen students’ understanding and ability to reason deductively, which is crucial for advanced mathematical thinking.
Benefits of Geometry Worksheets
Reinforce Learning
By providing additional practice outside of classroom lessons, geometry worksheets help students reinforce and solidify their understanding of geometric concepts. These worksheets offer a variety of problems that allow students to apply what they have learned in different contexts, thus deepening their comprehension. Regular practice with these problems ensures that students retain the information and can recall it when needed, reducing the risk of forgetting key concepts over time. Additionally, worksheets can bridge the gap between classroom learning and homework, making it easier for students to stay on track with their studies.
Assess Understanding
Teachers can use geometry worksheets to assess how well students have grasped specific topics. These assessments can take the form of quizzes, homework assignments, or in-class activities, providing teachers with valuable insights into their students’ strengths and weaknesses. By analyzing worksheet results, teachers can identify which concepts need further clarification and tailor their instruction accordingly. This targeted approach helps ensure that all students achieve a solid understanding of geometry, enabling them to progress confidently through more advanced topics.
Develop Problem-Solving Skills
Regular practice with a variety of problems helps students develop critical thinking and problem-solving skills. Geometry worksheets often present challenges that require students to think logically and creatively to find solutions. By working through these problems, students learn to approach complex tasks systematically, breaking them down into manageable steps. This skill set is not only essential for success in geometry but also valuable in other areas of mathematics and in everyday life, where problem-solving abilities are crucial.
Introduce New Concepts
Worksheets can introduce new geometric concepts in a gradual and structured manner. By presenting new material incrementally, worksheets help prevent students from feeling overwhelmed by too much information at once. This step-by-step approach allows students to build on their existing knowledge, making it easier to understand and retain new concepts. Additionally, worksheets often include visual aids and guided practice problems that provide clear examples and reinforce the learning process, facilitating a smoother transition to more complex topics.
Enhance Engagement
Interactive and visually appealing worksheets can increase student engagement and interest in geometry. Worksheets that incorporate colorful diagrams, real-world applications, and hands-on activities make learning more enjoyable and relatable for students. Engaging content helps maintain students’ attention and motivation, encouraging them to invest more effort in their studies. Furthermore, interactive elements such as puzzles, games, and collaborative exercises can make learning geometry feel less like a chore and more like an exciting challenge, fostering a positive attitude toward the subject.