Radius and Diameter Worksheets

About These 15 Worksheets

These worksheets will help students grasp and practice fundamental circle geometry concepts. These worksheets feature a variety of problems focusing on finding the radius, diameter, circumference, and area of circles. They cater to different learning levels, from basic identification and calculation tasks to more complex applications requiring a deeper understanding of geometric principles. These worksheets are essential resources for teachers to reinforce classroom instruction and for students to develop a solid foundation in geometry through structured practice.

What Are Radius and Diameter?

The radius of a circle is the distance from the center of the circle to any point on its circumference. It is a key geometric property that is half the length of the diameter, which spans the circle from one edge to the opposite edge, passing through the center. The diameter is twice the length of the radius and represents the longest distance across the circle. These measurements are fundamental in calculating other properties of the circle, such as its circumference and area.

Math Skills Explored

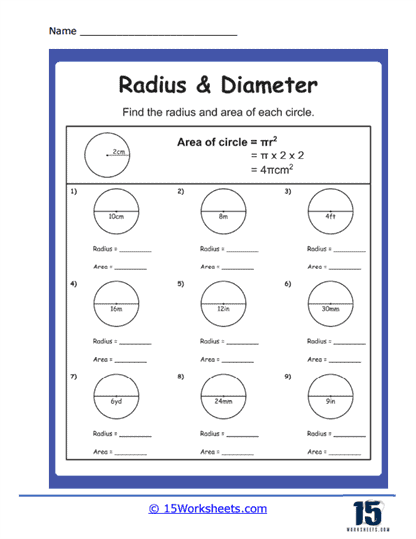
Radius and Diameter worksheets delve into several key math skills. They enhance students’ understanding of the basic properties of circles, such as the radius (distance from the center to any point on the edge) and diameter (twice the radius, spanning the circle through the center). Students practice using formulas to calculate the circumference and area of circles, applying the formulas for circumference (C = 2πr or C = πd) and area (A = πr²). These worksheets also often involve unit conversions, helping students handle different units of measurement and apply mathematical operations in various contexts.

Types of Exercises

Identifying Radius and Diameter

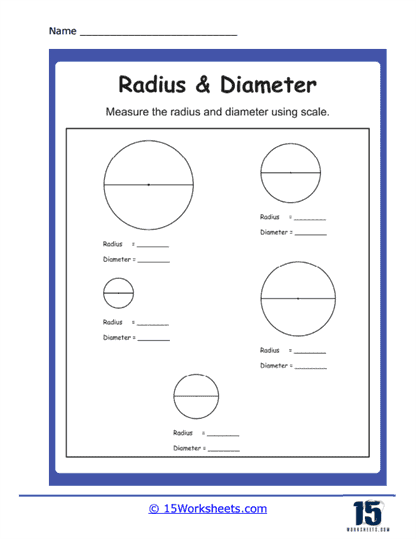
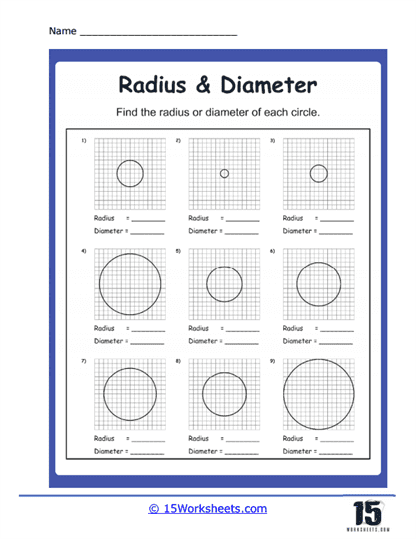
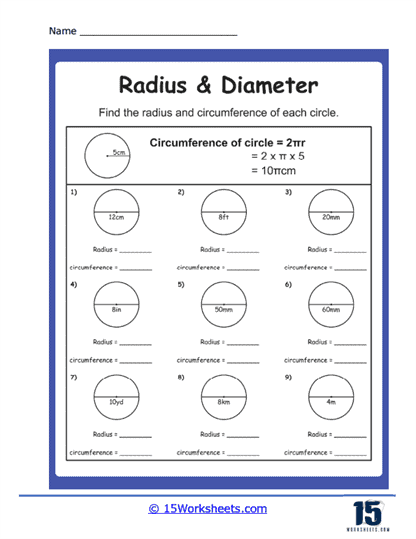
These problems require students to identify the radius and diameter in various circle diagrams. Students may be presented with circles where either the radius or diameter is marked, and they need to correctly label these parts. This type of problem helps students understand the definitions and visual representations of the radius and diameter, reinforcing their fundamental knowledge of circle geometry. Through these exercises, students become proficient in distinguishing between these two critical components of a circle.

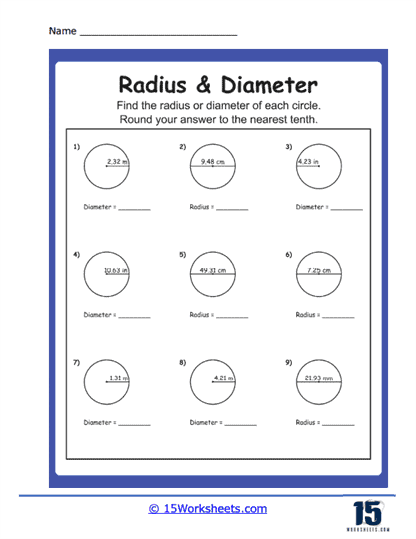
Calculating Radius from Diameter

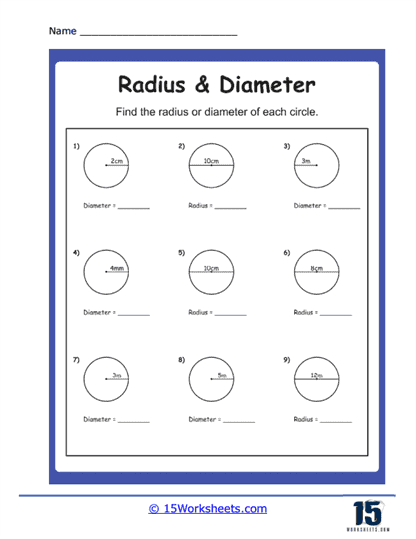
In these problems, students are given the diameter of a circle and must determine the radius. This requires understanding the relationship between the radius and diameter, specifically that the radius is half the length of the diameter. Such exercises help students practice basic arithmetic operations and develop an intuitive grasp of how changes in one measurement affect the other. This type of problem is crucial for building foundational skills in geometry and preparing students for more complex calculations involving circles.

Calculating Diameter from Radius

These problems present the radius of a circle and ask students to find the diameter. Here, students need to apply their understanding that the diameter is twice the length of the radius. These exercises reinforce the relationship between these two measurements and help students practice multiplication skills. They also emphasize the importance of understanding proportional relationships in geometry, which is a key concept in many advanced mathematical topics.

Word Problems Involving Real-World Contexts

Word problems integrate the concepts of radius and diameter into real-world scenarios, such as finding the size of a circular garden, a wheel, or a pizza. Students must extract the relevant information, understand the context, and apply their knowledge of radius and diameter relationships to solve the problem. These problems enhance critical thinking and demonstrate the practical applications of geometric concepts. They also improve students’ ability to translate everyday situations into mathematical terms, which is an essential skill for real-world problem-solving.

Drawing Circles with Given Radius or Diameter

In these problems, students are asked to draw circles with specified radii or diameters using a compass. This type of exercise helps students develop their geometric construction skills and reinforces their understanding of the spatial relationships within a circle. By physically drawing the circles, students gain a hands-on understanding of how the radius and diameter define the size and shape of the circle. This practical application also improves their precision and accuracy in geometric constructions.

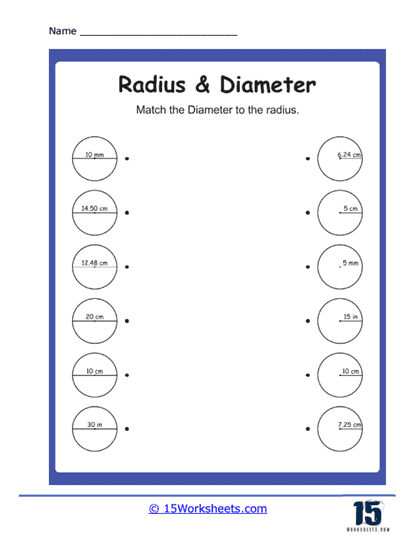
Comparing Radii and Diameters

Students are given multiple circles and must compare their radii and diameters to determine relationships such as which circle is larger or smaller. These problems enhance students’ ability to analyze and compare geometric figures based on their properties. Understanding how different measurements relate helps students develop a deeper comprehension of geometric principles. These comparison problems also prepare students for more complex geometric analyses and reasoning tasks.

Applications in Area and Circumference

While these problems do not directly calculate area or circumference, they lay the groundwork by asking students to identify and understand the roles of radius and diameter in these formulas. Problems might involve conceptual questions about how changing the radius or diameter would affect the area or circumference of a circle. This type of problem helps students see the broader implications of radius and diameter measurements and prepares them for future topics in circle geometry. Understanding these foundational concepts is crucial for mastering more advanced geometric calculations and applications.

Benefits of These Worksheets

Foundational Understanding of Circle Geometry

Radius and diameter worksheets provide students with a foundational understanding of circle geometry, which is essential for mastering more advanced mathematical concepts. By working through problems that require them to identify and label the radius and diameter, students become familiar with these key geometric terms and their visual representations. This foundational knowledge is crucial for understanding how circles are defined and measured, forming the basis for more complex topics such as area and circumference calculations.

Reinforcement of Basic Arithmetic Skills

These worksheets also reinforce basic arithmetic skills through problems that involve calculating the radius from the diameter and vice versa. Such exercises require students to perform simple division and multiplication, which strengthens their arithmetic abilities. By repeatedly applying these operations in a geometric context, students develop a stronger grasp of proportional relationships and numerical reasoning. This practice is beneficial not only for geometry but also for their overall mathematical proficiency.

Development of Critical Thinking and Problem-Solving Skills

Radius and diameter worksheets often include word problems that integrate real-world scenarios, encouraging students to apply their geometric knowledge to practical situations. These problems enhance critical thinking and problem-solving skills by requiring students to extract relevant information, understand the context, and determine the appropriate geometric relationships to find a solution. This process of translating everyday situations into mathematical terms helps students develop a deeper understanding of how geometric concepts are used in real life.

Improvement of Geometric Construction Skills

Drawing exercises included in these worksheets help students improve their geometric construction skills. By using a compass to draw circles with specified radii or diameters, students gain hands-on experience in creating precise geometric figures. This practical application reinforces their understanding of the spatial relationships within a circle and enhances their ability to perform accurate geometric constructions. Developing these skills is important for more advanced topics in geometry and for practical tasks in fields such as engineering and design.

Enhancement of Analytical and Comparative Skills

Worksheets that involve comparing the radii and diameters of different circles help students develop their analytical and comparative skills. These problems require students to analyze geometric figures based on their properties and make comparisons to determine relationships such as size and proportion. Understanding how different measurements relate to each other helps students build a deeper comprehension of geometric principles. These analytical skills are essential for more complex geometric analyses and reasoning tasks.

Preparation for Advanced Geometric Calculations

By laying the groundwork for understanding the roles of radius and diameter in calculations of area and circumference, these worksheets prepare students for more advanced geometric topics. Problems that explore the implications of changing the radius or diameter help students see the broader applications of these measurements. This preparation is crucial for mastering advanced calculations and for understanding the geometric properties of circles in greater depth. Developing a strong foundation in these basic concepts ensures that students are well-equipped for future mathematical challenges.

Encouragement of Independent Learning

Radius and diameter worksheets encourage independent learning by providing a structured yet flexible framework for students to practice and apply their geometric knowledge. These worksheets offer a variety of problems that challenge students to think critically and solve problems on their own. By working through these exercises independently, students develop confidence in their abilities and become more self-reliant learners. This independence is a valuable skill that will benefit them throughout their academic careers and beyond.

Real World Uses of These Concepts

Fundamental Measurements in Various Fields

Understanding the concepts of radius and diameter is crucial in the real world because these measurements are fundamental in various fields. In engineering and manufacturing, precise measurements of circular components like gears, pipes, and wheels are essential for designing and producing functional and reliable products. The radius and diameter help determine the size, fit, and function of these parts, ensuring that machinery operates smoothly and safely. Without a solid understanding of these concepts, it would be challenging to achieve the precision required in these industries.

Architectural and Construction Applications

In architecture and construction, the concepts of radius and diameter are used to design and construct various structures and features. For instance, when designing curved walls, arches, or circular windows, knowing the radius and diameter ensures that these elements are proportionate and structurally sound. These measurements also play a role in landscaping, where circular garden beds, fountains, and pathways must be accurately sized to fit within the overall design. Understanding these concepts helps architects and builders create aesthetically pleasing and functional spaces.

Everyday Practical Uses

In everyday life, understanding the radius and diameter can be very practical. For example, when baking, knowing the diameter of a cake pan helps in scaling recipes accurately. Similarly, when buying a new tire or a round table, understanding these measurements helps ensure a proper fit and function. These concepts are also useful in activities like crafts and DIY projects, where creating accurate circular shapes and designs can be important for the success of the project.

Scientific and Mathematical Applications

In science and mathematics, the concepts of radius and diameter are fundamental for understanding and exploring various phenomena. In physics, these measurements are crucial for studying the properties of circular motion, waves, and orbits. In biology, understanding the radius and diameter of cells, blood vessels, and other circular structures helps in studying their functions and behaviors. In mathematics, these concepts are foundational for exploring more advanced topics in geometry, trigonometry, and calculus, where precise measurements and relationships are essential.

Enhancing Spatial Awareness and Problem-Solving Skills

Understanding the radius and diameter enhances spatial awareness and problem-solving skills. These concepts help individuals visualize and comprehend the properties of circular objects and their relationships with other shapes. This spatial reasoning is critical in various tasks, from arranging furniture in a room to designing complex machinery. Moreover, solving problems involving radius and diameter helps develop logical thinking and analytical skills, which are valuable in both academic and real-world problem-solving scenarios.

Contributions to Innovation and Design

Knowledge of radius and diameter contributes significantly to innovation and design. Whether creating new products, developing architectural marvels, or designing efficient transportation systems, understanding these concepts allows for creativity and precision. Innovators and designers can use this knowledge to push the boundaries of what is possible, creating solutions that are both functional and groundbreaking. The ability to accurately measure and manipulate circular dimensions is a key component in turning visionary ideas into reality.

Example problem: A circular garden has a circumference of 31.4 meters. What is the diameter of the garden?

Step-by-Step Solution

1. Understand the formula: The circumference C of a circle is given by the formula:

C = π x d

where π (pi) is approximately 3.14, and d is the diameter of the circle.

2. Substitute the given value: You are given the circumference C=31.4 meters. Substitute this value into the formula:

31.4 = 3.14 x d

3. Solve for d: To find the diameter d, divide both sides of the equation by π (3.14):

d= 3.14/31.4
​
4. Calculate the result: d = 10

Conclusion: The diameter of the garden is 10 meters.