Angles Worksheets
About These 15 Worksheets
These worksheets in geometry provide a comprehensive and effective means for students to understand and master the various properties and relationships associated with angles. Through a diverse range of exercises and problems, these worksheets enhance students’ geometric understanding, problem-solving skills, algebraic proficiency, visual and spatial reasoning, and mathematical communication. Understanding angles is crucial for success in advanced mathematics and numerous real-world applications, making it an essential component of a well-rounded education. By developing a strong foundation in angles, students are better prepared for academic challenges and practical tasks, equipping them with valuable skills for their future endeavors.
Angle worksheets are an essential tool in the study of geometry, designed to help students understand and master the various properties and relationships associated with angles. These worksheets encompass a wide range of exercises and problems that facilitate learning through practice, visualization, and application of geometric concepts. Understanding angles is crucial for students as it forms the foundation for more advanced mathematical topics and is applicable in numerous real-world scenarios.
Types of Exercises
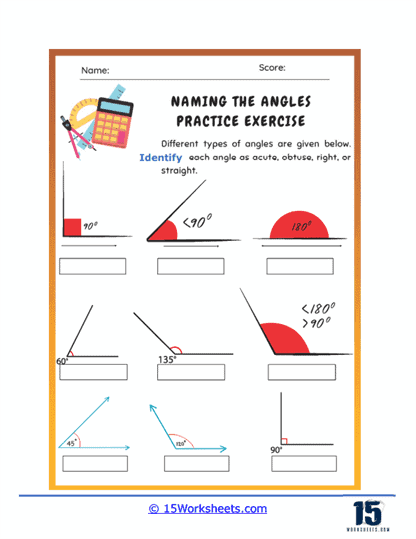
Identifying and Naming Angles – One of the basic exercises found on angle worksheets involves identifying and naming angles. Students are presented with diagrams of various geometric figures and asked to identify angles based on their position and notation. This exercise helps students become familiar with different types of angles, such as acute, obtuse, right, straight, and reflex angles. By practicing this skill, students learn to recognize angles and understand their properties, which is fundamental for further study in geometry.
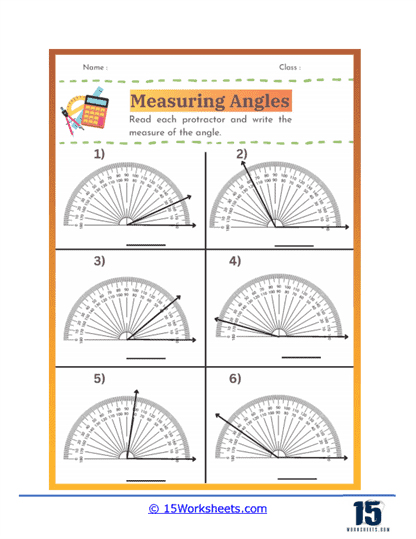
Measuring Angles – Measuring angles is a key component of angle worksheets. Students use protractors to measure the degree of given angles accurately. This exercise teaches students how to properly align the protractor with the vertex and arms of the angle, read the measurement, and record it correctly. Measuring angles is crucial for developing precision and attention to detail, skills that are valuable in both academic and real-world contexts.
Classifying Angles – Classifying angles based on their measures is another common exercise. Students are asked to categorize angles as acute, obtuse, right, straight, or reflex. This classification helps students understand the different types of angles and their properties. It also reinforces their ability to compare and contrast angles based on their measurements, enhancing their overall geometric understanding.
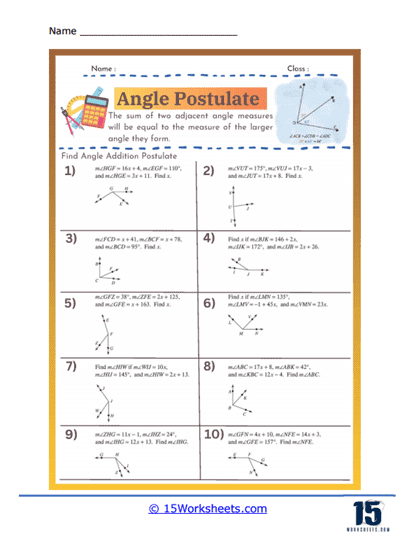
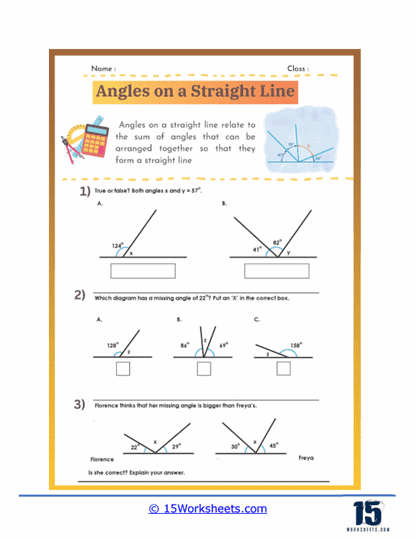
Complementary and Supplementary Angles – Worksheets often include problems involving complementary and supplementary angles. Complementary angles are two angles whose measures add up to 90 degrees, while supplementary angles add up to 180 degrees. Students practice identifying these angles in various geometric configurations and solving for unknown angle measures. These exercises help students understand the relationships between angles and develop their problem-solving skills.
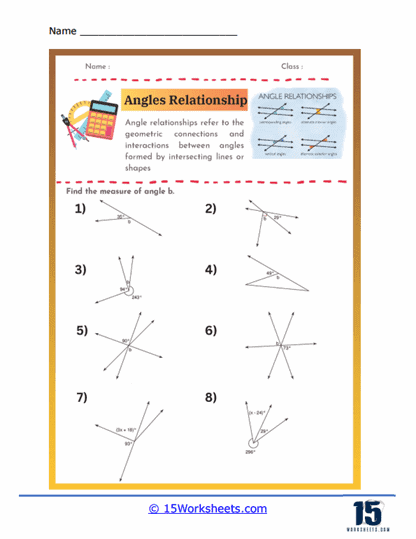
Vertical and Adjacent Angles – Problems involving vertical and adjacent angles are also common on angle worksheets. Vertical angles are the pairs of opposite angles formed when two lines intersect, and they are always congruent. Adjacent angles share a common vertex and a common side but do not overlap. Students are given diagrams of intersecting lines and asked to identify and measure vertical and adjacent angles. These exercises reinforce students’ understanding of angle relationships and help them practice identifying and measuring angles in various geometric configurations.
Angles Formed by Parallel Lines and a Transversal – A more advanced type of problem involves angles formed by parallel lines and a transversal. When a transversal intersects two parallel lines, it creates several angle pairs, including corresponding, alternate interior, alternate exterior, and consecutive interior angles. Students are asked to identify these angles and use their properties to calculate unknown angle measures. This type of exercise helps students understand the properties of angles in parallel line configurations and apply this knowledge to solve complex problems.
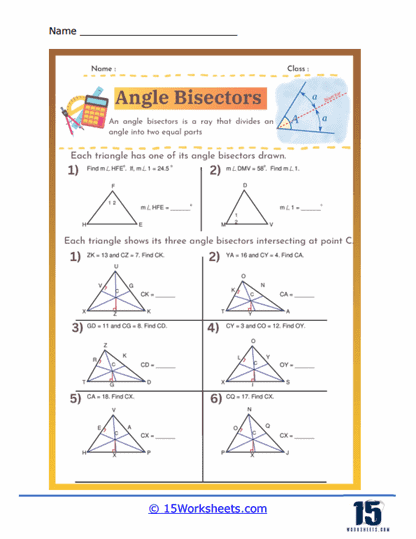
Angle Bisectors and Perpendicular Bisectors – Worksheets might include problems that require students to draw and identify angle bisectors and perpendicular bisectors. These exercises involve using a compass and straightedge to accurately bisect given angles or line segments, reinforcing students’ skills in geometric constructions. By practicing these constructions, students learn to divide angles and segments into equal parts, which is crucial for developing spatial reasoning and precision in geometric work.
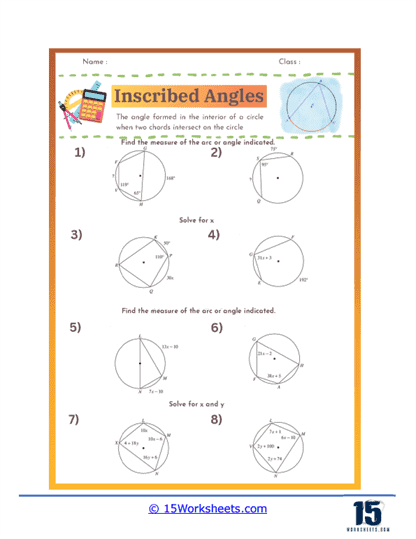
Inscribed Angles and Arcs – Inscribed angle worksheets help students understand the relationships between inscribed angles and the arcs they intercept. These exercises often involve identifying inscribed angles, calculating their measures, and understanding their properties. Students might be asked to prove that inscribed angles intercepting the same arc are congruent or to use inscribed angles to solve for unknown measures in geometric figures. These problems reinforce key geometric concepts and enhance students’ ability to work with circles and angles.
Real-World Application Problems – Many angle worksheets include real-world application problems where students must apply their geometric knowledge to practical scenarios. For example, students might be asked to determine the angles needed to construct a piece of furniture, design a garden layout, or analyze the angles in architectural designs. These problems require students to use their angle measurement skills in realistic contexts, demonstrating the relevance and importance of geometry in everyday life.
Estimating Angles – Some worksheets might include angle estimation exercises, where students are asked to estimate the measure of given angles without using a protractor. These problems develop students’ ability to visually assess and approximate angle measures, which is a valuable skill in both academic and real-life contexts. Estimating angles helps students develop a better intuitive understanding of angles and their relationships.
Solving for Unknown Angles Using Algebra – Angle worksheets often integrate algebraic concepts by requiring students to set up and solve equations based on angle relationships. For example, students might be given expressions for the measures of complementary or supplementary angles and asked to solve for a variable. These exercises help students understand the connection between algebra and geometry and reinforce their algebraic skills.
Angle Proofs – Advanced worksheets may include angle proofs, where students are required to use logical reasoning and geometric properties to prove statements about angles. These proofs might involve demonstrating that certain angles are congruent, that angle bisectors create equal angles, or that the sum of angles in a polygon meets specific criteria. Angle proofs help students develop critical thinking skills and a deeper understanding of geometric principles.
The Importance of Understanding Angles
Understanding everything we can about angle geometry is crucial for several reasons, spanning from foundational mathematical knowledge to practical real-world applications. Here’s an in-depth look at why mastering angle geometry is so important:
Building Blocks of Geometry – Angles are fundamental to the study of geometry, serving as the building blocks for more complex geometric concepts. They form the basis of understanding shapes, structures, and the relationships between different geometric elements. Without a solid grasp of angles, it becomes challenging to progress to more advanced topics such as polygons, circles, and three-dimensional shapes.
Precursor to Advanced Mathematics – A thorough understanding of angles is essential for delving into advanced mathematical fields such as trigonometry, calculus, and linear algebra. For instance, trigonometry revolves around the relationships between angles and sides of triangles, while calculus often involves analyzing the slopes of curves (essentially angles). Mastering angle geometry ensures that students have the necessary foundation to succeed in these higher-level courses.
Analytical and Critical Thinking -Working with angles helps develop analytical thinking skills. Solving problems involving angles requires students to break down complex problems into simpler parts, identify relationships, and apply logical reasoning to arrive at solutions. This analytical approach is beneficial not only in mathematics but also in other academic disciplines and everyday life.
Geometry problems often involve proofs and justifications, where understanding angles is crucial. By learning to prove the properties of angles and their relationships, students enhance their critical thinking skills. This ability to think critically is valuable across various fields, from scientific research to law, where constructing logical arguments and solving complex problems are key.
Visualization Skills – Understanding angles enhances students’ visualization skills. The ability to visualize geometric shapes and their relationships is crucial for solving problems in geometry and other fields. Improved visualization skills help students understand abstract concepts and apply them in various contexts, from mathematics to art.
Spatial Awareness – Angles are integral to spatial reasoning, which involves understanding and manipulating objects in space. Spatial reasoning skills are important in many fields, including engineering, architecture, robotics, and computer graphics. By mastering angles, students develop the ability to navigate and interpret three-dimensional spaces effectively.
Real-World Applications
Engineering and Architecture – In fields like engineering and architecture, precise knowledge of angles is indispensable. Engineers use angles to design and analyze the structural integrity of buildings, bridges, and machinery. Architects rely on angles to create aesthetically pleasing and functional designs. Understanding angles ensures that structures are safe, stable, and visually appealing.
Construction and Carpentry – In construction and carpentry, angles are crucial for creating accurate and functional projects. Carpenters need to measure and cut wood at precise angles to ensure that pieces fit together correctly. Knowledge of angles helps in creating joints, framing structures, and achieving the desired shapes in construction projects.
Navigation and Surveying – Angles play a vital role in navigation and surveying. Navigators use angles to chart courses, determine directions, and calculate distances. Surveyors measure angles to map out land, determine property boundaries, and plan construction projects. Accurate angle measurements are essential for ensuring that navigation routes are safe and that land measurements are precise.
Art and Design – In art and design, understanding angles is essential for creating accurate and proportionate works. Artists use angles to create perspectives and achieve realistic proportions in their drawings and paintings. Designers rely on angles to create balanced and harmonious compositions in graphic design, interior design, and fashion design.
Understanding everything we can about angle geometry is essential for building a strong foundation in mathematics, enhancing problem-solving skills, and applying geometric principles to real-world scenarios. Mastery of angles supports interdisciplinary learning, develops visual and spatial reasoning, and improves mathematical communication. By studying angles, students build confidence in their mathematical abilities and gain valuable skills for lifelong learning and success in various fields. The importance of angles extends beyond the classroom, influencing numerous aspects of our daily lives and professional endeavors.