Transformation Worksheets
About These 15 Worksheets
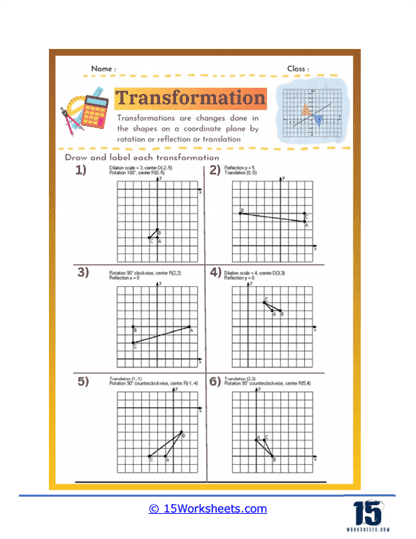
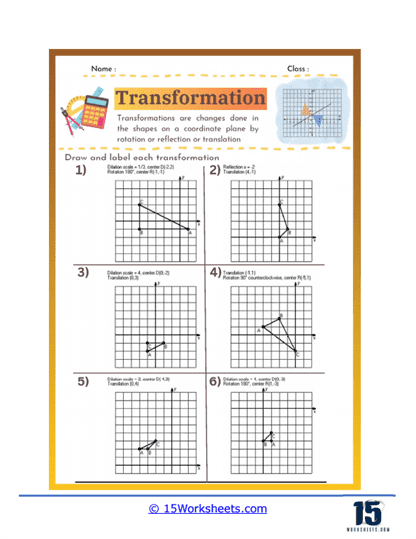
These worksheets will help students understand geometric transformations on a coordinate plane. These transformations include translations (sliding a shape), rotations (turning a shape around a point), reflections (flipping a shape over a line), and dilations (resizing a shape). By working through these worksheets, students gain a solid grasp of how these transformations affect the position, orientation, and size of geometric figures. Transformation worksheets typically involve plotting points, drawing transformed figures, and analyzing the relationships between the original and transformed shapes.
What Are Transformations in Geometry?
In geometry, a transformation is an operation that moves, flips, or changes a shape in some way while preserving certain properties, such as size, shape, and angles, through processes like translation (sliding), rotation (turning), reflection (flipping), and dilation (resizing).
Math Skills Explored
Understanding Geometric Transformations
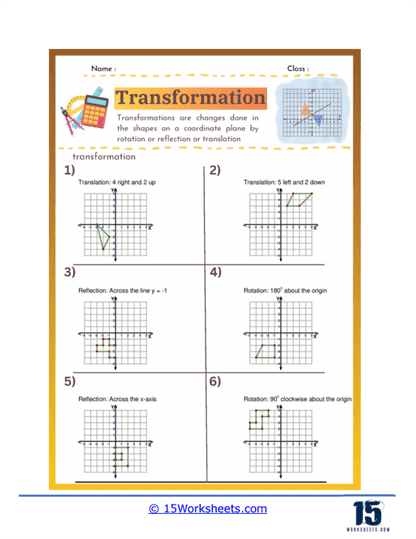
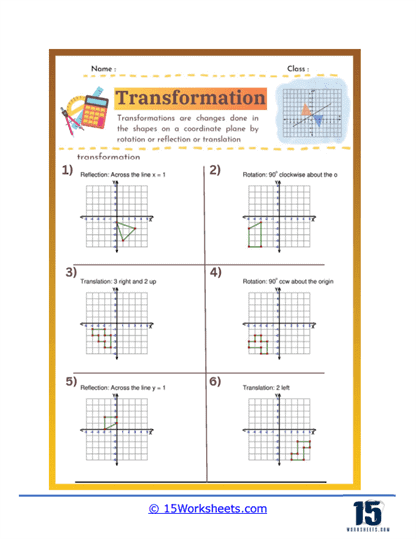
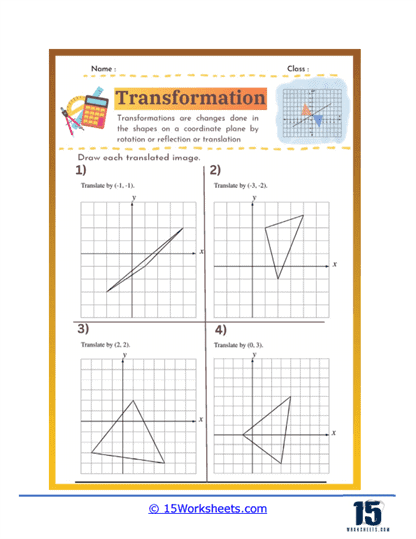
Translation – Translation involves sliding a shape from one position to another without rotating or flipping it. Worksheets focused on translation help students understand the concept of moving shapes along a straight path and how to determine the new coordinates of a shape’s vertices after a translation. These exercises reinforce students’ ability to work with vectors and coordinate systems.
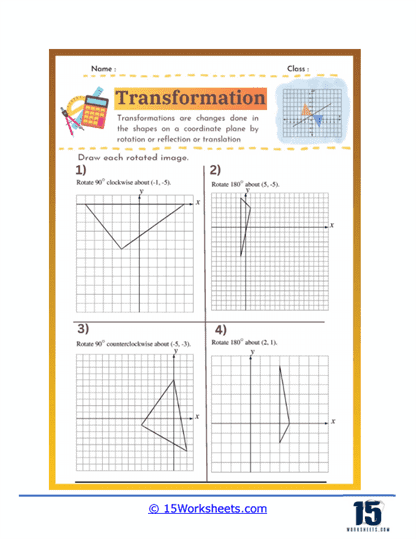
Rotation – Rotation requires turning a shape around a fixed point, usually the origin or a point on the shape. Worksheets on rotation help students grasp how to rotate shapes by specific angles, such as 90°, 180°, or 270°, and understand the resulting position of the shape. This skill helps students understand angular displacement and the effects of rotation on shapes in a plane.
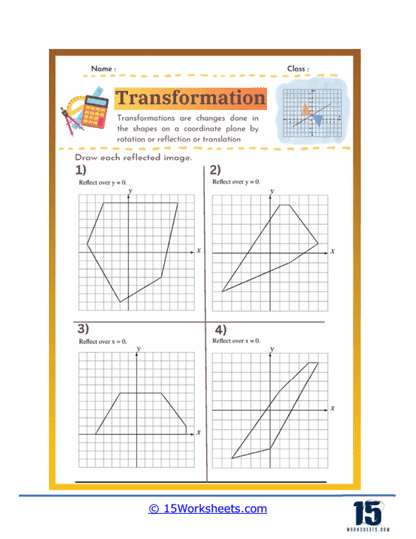
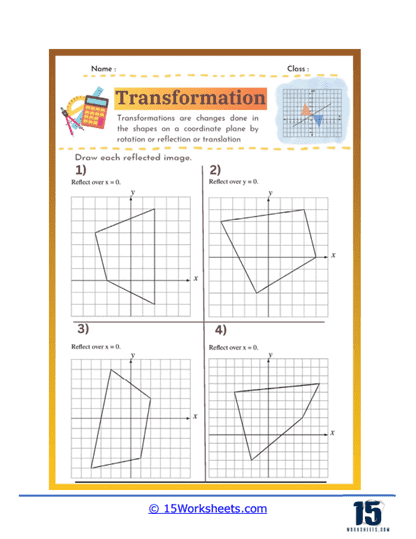
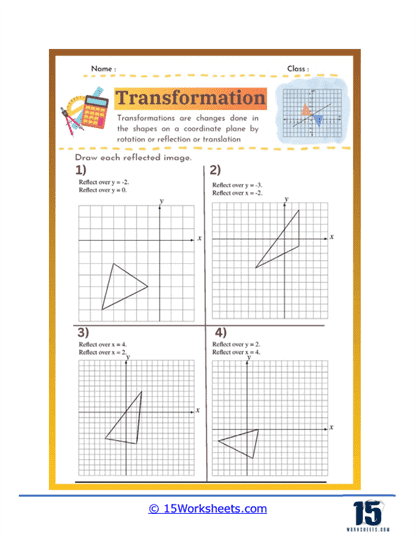
Reflection – Reflection involves flipping a shape over a line, such as the x-axis, y-axis, or another line in the plane. Reflection worksheets help students learn how to create mirror images of shapes and understand the concept of symmetry. These exercises develop students’ ability to use coordinate transformations and recognize symmetrical properties in geometric figures.
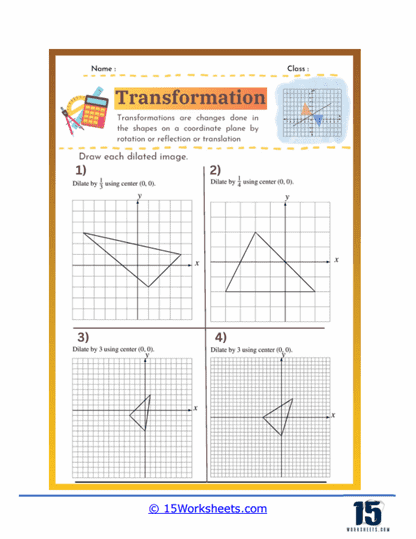
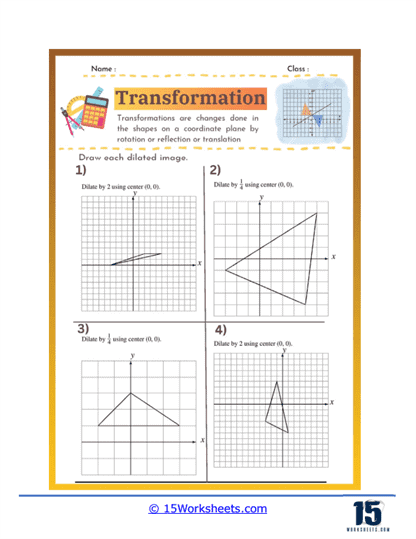
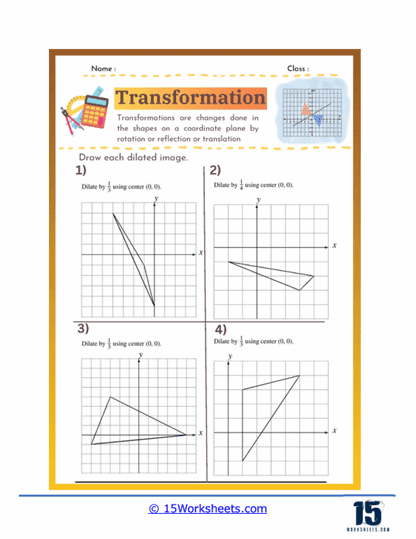
Dilation – Dilation involves resizing a shape while keeping its proportions constant, typically around a fixed center point. Worksheets on dilation help students understand the principles of scaling shapes up or down and the impact on the coordinates of the shape’s vertices. This skill is crucial for understanding similarity and proportional reasoning in geometry.
Developing Spatial Reasoning and Visualization
Spatial Awareness – By working with transformation worksheets, students enhance their spatial awareness and ability to visualize how shapes move and change in space. This skill is vital for understanding more complex geometric concepts and for applications in fields such as architecture, engineering, and computer graphics.
Coordinate Geometry – Transformation worksheets often require students to work within a coordinate plane, reinforcing their understanding of coordinate geometry. Students learn to plot points, interpret coordinates, and apply transformations to these points, which are essential skills for solving a wide range of geometric problems.
Reinforcing Mathematical Rigor and Precision
Accuracy and Precision – These worksheets demand a high level of accuracy and precision as students perform transformations and determine the new positions of shapes. This practice helps students develop meticulous attention to detail, which is important for mathematical problem-solving and for technical fields requiring precise measurements.
Logical Reasoning – Working through transformations requires logical reasoning and the ability to follow a sequence of steps accurately. Students must understand the rules governing each transformation and apply them systematically, which strengthens their problem-solving and critical thinking skills.
Applying Geometric Principles to Real-World Contexts
Real-World Applications – Many transformation worksheets include problems set in real-world contexts, such as designing patterns, navigating maps, or modeling physical objects. These exercises help students see the relevance of geometric transformations in everyday life and various professional fields, enhancing their motivation to learn and apply these concepts.
Symmetry and Patterns – Understanding transformations allows students to recognize and create symmetrical patterns, which are commonly found in art, design, and nature. This knowledge is useful for fields such as graphic design, where creating balanced and visually appealing compositions is crucial.
Types of Exercises On These Worksheets
Transformation worksheets come with a variety of exercises and practice problems that cater to different aspects of geometric transformations. Here are the types of problems typically found in these worksheets:
Translations
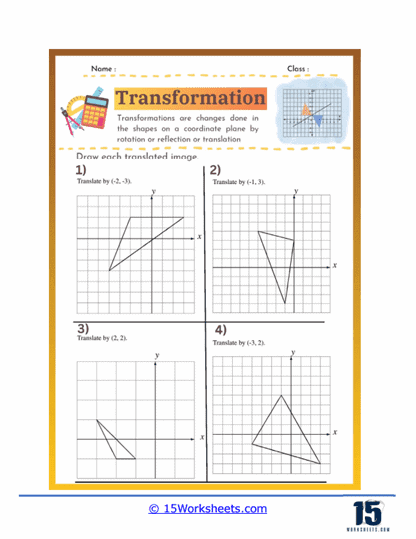
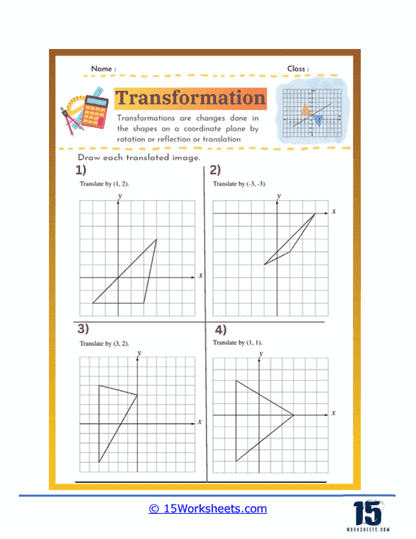
Translation exercises involve sliding a shape from one position to another without altering its orientation or size. Students are usually given a shape with specific coordinates and a vector indicating how far and in which direction to move the shape. For example, a problem might ask students to translate a triangle by a vector (3, -2), meaning they should move the shape 3 units to the right and 2 units down.
Rotations
Rotation problems require students to turn a shape around a specific point, usually the origin or a vertex of the shape. The exercises specify the angle and direction of rotation, such as 90 degrees clockwise or 180 degrees counterclockwise. Students must apply the rotation rule to each vertex of the shape and plot the new coordinates to see the rotated shape.
Reflections
Reflection exercises focus on flipping a shape over a specified line, such as the x-axis, y-axis, or another line like y = x. Students must determine the new positions of the shape’s vertices by using the reflection rules. For instance, reflecting a point (x, y) over the y-axis results in the point (-x, y).
Dilations
Dilation problems involve resizing a shape either by enlarging or reducing it based on a scale factor. The center of dilation is typically the origin or another specified point. Students need to apply the dilation formula to each vertex of the shape to determine the new size and position.
Combined Transformations
Some worksheets present problems that involve multiple transformations. For example, a shape might first be translated, then rotated, and finally reflected. These exercises challenge students to apply a sequence of transformations and understand how each step affects the overall result.
Identifying Transformations
In addition to performing transformations, students may also encounter exercises that require them to identify the type of transformation applied to a given shape. These problems help reinforce the characteristics of each transformation and ensure that students can recognize them in various contexts.
Real World Applications and Career Fields
Architecture and Urban Planning
Transformations are widely used in architecture and urban planning to design buildings, layouts, and cityscapes. Architects use reflections, rotations, and translations to create symmetrical building designs and aesthetic patterns. For instance, symmetrical facades are often designed using reflections, while rotations can help in creating repetitive patterns in architectural elements like windows and columns. Urban planners use translations to replicate street layouts and park designs across different parts of a city, ensuring consistency and coherence in urban development.
Engineering and Manufacturing
In engineering and manufacturing, transformations are essential for designing and producing parts that fit together precisely. Engineers use geometric transformations to rotate and translate parts in CAD (Computer-Aided Design) software, ensuring that components align correctly in assembly processes. For example, designing gears, bolts, and machine parts often involves rotating and translating shapes to fit within larger mechanical systems. Understanding these transformations ensures that parts are manufactured with exact specifications, reducing errors and improving efficiency in production lines.
Computer Graphics and Animation
Transformations are fundamental in computer graphics and animation for creating and manipulating digital images and models. In computer graphics, transformations like translation, rotation, and scaling are used to move, rotate, and resize objects within a scene. These transformations are crucial for rendering 3D models, animating characters, and creating visual effects. For example, animators use rotations to simulate natural movements of characters, while translations help in moving objects smoothly across a scene. Understanding these transformations allows for the creation of realistic and dynamic digital environments.
Robotics and Automation
In robotics and automation, transformations are used to program and control the movement of robots and automated systems. Robots use translations and rotations to navigate environments, manipulate objects, and perform tasks accurately. For example, a robotic arm might use a series of rotations to position itself correctly and translations to move objects from one place to another. Understanding transformations ensures that robots can perform complex tasks with precision, which is essential in industries like manufacturing, healthcare, and logistics.
Geographic Information Systems (GIS) and Mapping
Transformations are critical in Geographic Information Systems (GIS) and mapping for analyzing spatial data and creating accurate maps. GIS professionals use translations, rotations, and scaling to align and overlay different map layers, ensuring that spatial data is accurately represented. For example, transforming satellite images to align with geographical coordinates involves translating and rotating the images. Understanding these transformations allows for precise mapping, spatial analysis, and better decision-making in fields like environmental management, urban planning, and disaster response.
Art and Design
Artists and designers use transformations to create visually appealing and balanced artworks. In graphic design, transformations like reflections and rotations are used to create symmetrical patterns and designs. For instance, logos and graphic elements often incorporate rotational symmetry to achieve harmony and balance. In fine arts, transformations help artists experiment with different perspectives and compositions, enhancing the visual impact of their work. Understanding transformations allows artists and designers to create intricate and captivating designs.
Medical Imaging and Diagnostics
Transformations play a significant role in medical imaging and diagnostics for interpreting and analyzing medical images. Techniques like MRI, CT scans, and X-rays produce images that healthcare professionals must manipulate to diagnose conditions accurately. Transformations such as translations, rotations, and scaling help in aligning and comparing images from different angles and time points. Understanding these transformations allows for accurate analysis and better diagnosis, which is crucial for effective medical treatment and care.