Circumference Worksheets
About These 15 Worksheets
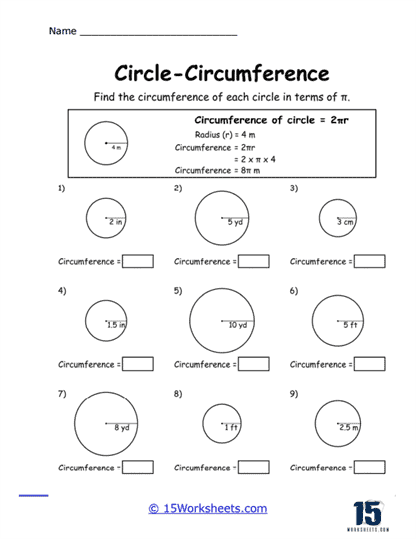
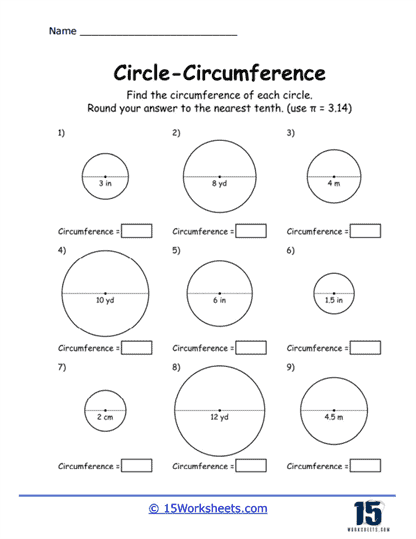
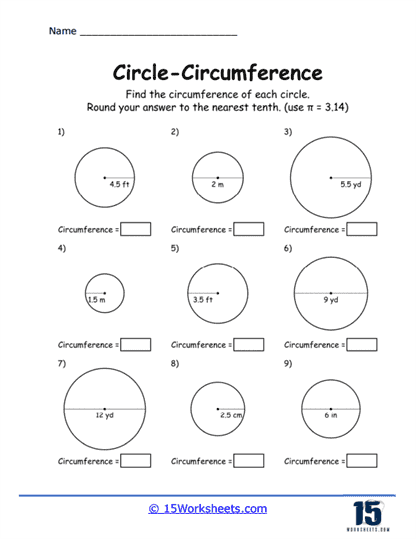
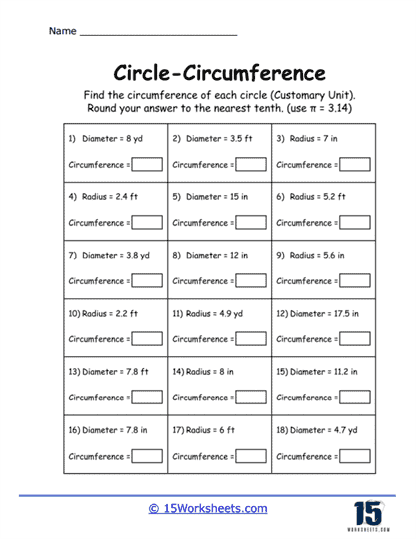
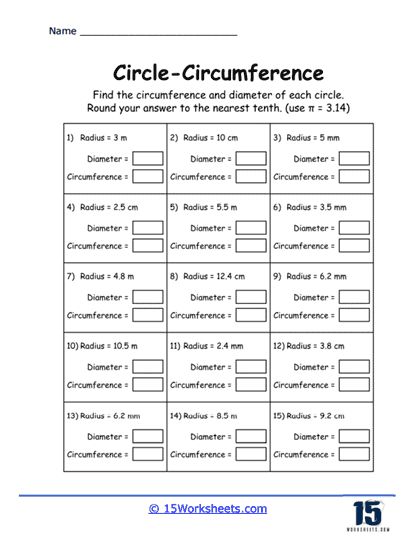
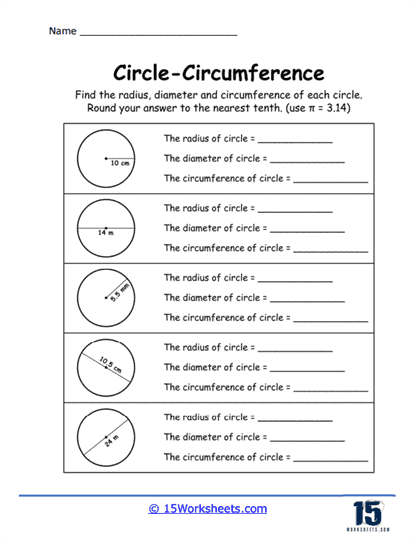
These worksheets can be used to help students understand and practice the concept of the circumference of a circle. These worksheets typically present a variety of problems that require students to apply mathematical formulas to find the circumference, given different pieces of information such as the radius or diameter of a circle. The primary formula used in these exercises is C = 2πr or C = πd, where C represents the circumference, π (pi) is approximately 3.14, r is the radius, and d is the diameter. These worksheets are essential for reinforcing the foundational concepts of geometry and ensuring students are comfortable with basic arithmetic operations involving circles.
What is Circumference?
Circumference is the distance around the edge or perimeter of a circle. It is a linear measurement, similar to the perimeter of other geometric shapes.
The concept of circumference is important in various fields, including geometry, engineering, and everyday life, such as when determining the distance around circular objects like wheels, coins, or circular tracks.
Benefits of These Worksheets
Circumference worksheets offer numerous benefits to students learning geometry. They help solidify the understanding of circle-related formulas and concepts, which are fundamental in mathematics. By regularly practicing with these worksheets, students improve their ability to solve real-world problems involving circular objects, enhancing their problem-solving and critical-thinking skills. These worksheets also help students develop precision and accuracy in their calculations, which are crucial skills in both academic and everyday contexts. Additionally, practicing with circumference worksheets prepares students for more advanced topics in mathematics and related fields such as engineering, physics, and architecture.
Math Skills Explored
Understanding and Using Formulas – Students learn to apply the formulas for the circumference of a circle. They become adept at identifying the necessary components (radius or diameter) and accurately substituting them into the formulas.
Arithmetic Operations – These worksheets often require multiplication and division, which helps students practice and refine these basic arithmetic skills.
Algebraic Manipulation – In more advanced exercises, students might need to rearrange formulas to solve for unknown variables, such as finding the radius or diameter given the circumference.
Measurement Units – Students gain experience working with different units of measurement, such as centimeters, meters, inches, and feet. This helps them understand the importance of unit consistency in calculations.
Rounding and Precision – Many circumference problems require students to round their answers to a specific decimal place, enhancing their understanding of significant figures and precision in mathematics.
Types of Exercises
Circumference worksheets include a variety of exercises to cater to different learning levels and to address multiple aspects of understanding and applying the circumference concept. Below are some common types of exercises and practice problems found in these worksheets:
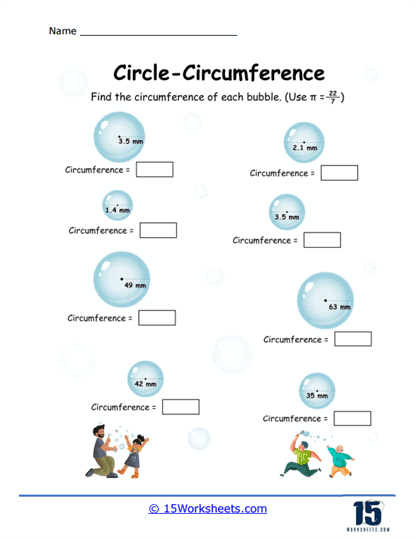
Basic Calculation Problems – These problems provide the radius or diameter of a circle and ask students to calculate the circumference using the appropriate formula. For example, “Find the circumference of a circle with a radius of 5 cm.”
Word Problems – These problems present real-world scenarios where students must apply their knowledge to find the circumference. For example, “A circular garden has a diameter of 10 meters. What is the length of the fence needed to surround the garden?”
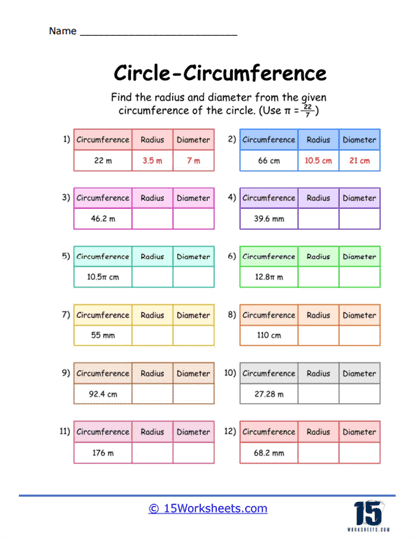
Missing Variable Problems – These problems provide the circumference and require students to work backward to find the radius or diameter. For example, “The circumference of a circle is 31.4 cm. What is the radius?”
Conversion Problems – These exercises require students to convert units before calculating the circumference. For example, “Find the circumference of a circle with a radius of 2.5 inches. Round your answer to the nearest tenth.”
Pi Estimation Problems – These problems emphasize the use of π and might provide it as a fraction (22/7) or as 3.14. For example, “Use π=22/7 to find the circumference of a circle with a diameter of 14 cm.”
Multi-step Problems – These involve more complex scenarios requiring multiple steps to solve. For example, “A circular track has a diameter of 400 meters. If you run around it 5 times, what is the total distance covered?”
Real-World Applications
Understanding the circumference of a circle is crucial in various professional fields. For instance, engineers frequently need to calculate the circumference of circular components in machinery to ensure proper fitting and function. Architects and designers use these calculations when planning structures that incorporate circular elements, such as domes or round windows. In the field of construction, knowing how to determine the circumference is essential for tasks like laying out circular foundations or planning road systems that include roundabouts.
In manufacturing, technicians often work with cylindrical objects where knowing the circumference is necessary for processes like cutting materials to precise lengths or fitting components together. Even in the realm of everyday business, understanding circumference can be crucial. For example, event planners may need to calculate the amount of material required to create circular decorations or the length of fencing needed to enclose a circular event space.
Understanding circumference is important in everyday use for several practical reasons:
Measurement and Construction
In construction and carpentry, accurately measuring the circumference of circular objects is crucial. For example, when creating circular tables, wheels, or columns, knowing the circumference helps ensure precision in cutting materials and fitting parts together seamlessly. This ensures stability, functionality, and aesthetics in various projects.
Fitness and Health
In fitness and health, understanding circumference is essential for measuring body parts, such as the waist, hips, and chest, to monitor changes in body size and shape. These measurements are used to assess fitness progress, health risks (e.g., waist circumference as an indicator of obesity), and tailor workout programs.
Engineering and Manufacturing
In engineering and manufacturing, calculating the circumference is vital for designing and producing circular objects like gears, pipes, and containers. Precise measurements are necessary to ensure parts fit together correctly, operate smoothly, and maintain safety standards. For example, engineers need to know the circumference of a wheel to design appropriate treads and to ensure proper rotation and balance.
Everyday Tasks
Even in simple everyday tasks, understanding circumference can be helpful. When wrapping gifts or decorating cakes, knowing the circumference allows you to cut ribbons or icing strips to the correct length. This knowledge can also be useful for gardening, such as determining the amount of fencing needed to enclose a circular garden bed.
Sports and Recreation
In sports, the concept of circumference is used to determine the size of balls and tracks. For instance, the circumference of a basketball or soccer ball is standardized to ensure consistency in gameplay. Similarly, measuring the circumference of running tracks ensures athletes cover the correct distances during training and competitions.
Transportation
In transportation, knowing the circumference of tires is crucial for vehicle maintenance and performance. The circumference affects the distance traveled per rotation and impacts speedometer accuracy, fuel efficiency, and overall driving safety. For cyclists, understanding tire circumference helps in calibrating cycle computers and improving riding efficiency.