Parallel Lines and Transversals Worksheets
About These 15 Worksheets
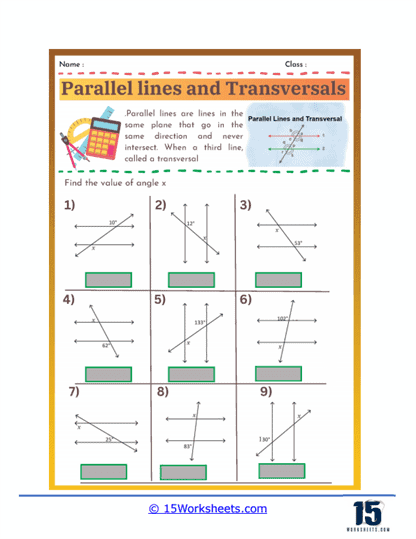
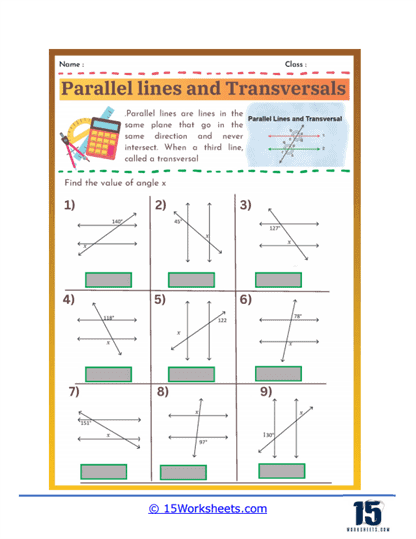
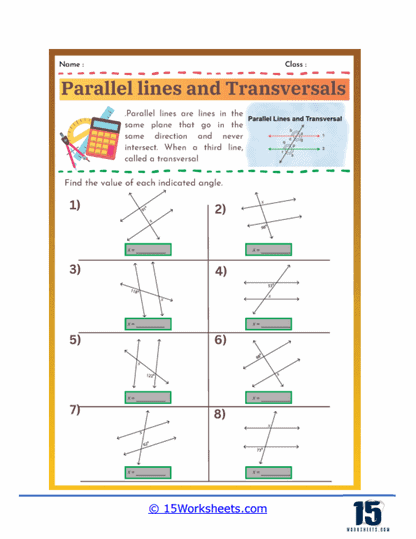
These worksheets teach and reinforce the understanding of geometric relationships between parallel lines and the angles formed when they are intersected by a transversal. A transversal is a line that crosses at least two other lines. When it intersects parallel lines, it creates various types of angles that have specific relationships and properties. These worksheets typically contain a variety of exercises designed to help students identify and calculate these angles, providing a solid foundation in geometry.
These worksheets include a variety of problems that challenge students to use geometric theorems and properties to find unknown angles, determine whether lines are parallel, and classify angle pairs. By engaging with these worksheets, students can develop a deep understanding of the relationships between angles formed by parallel lines and transversals. They also gain proficiency in using geometric postulates and theorems to solve problems, which are critical skills for more advanced studies in mathematics and related fields.
The Math Skills Explored
The primary math skills explored in parallel lines and transversals worksheets include understanding and applying properties of angles, recognizing different types of angles, and solving for unknown angle measures. Here are some key skills that students develop through these worksheets:
Identifying Angle Types
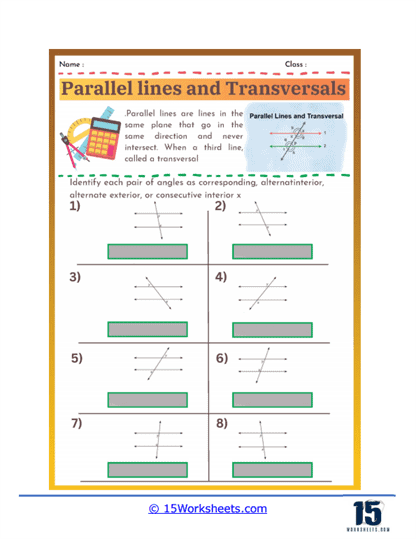
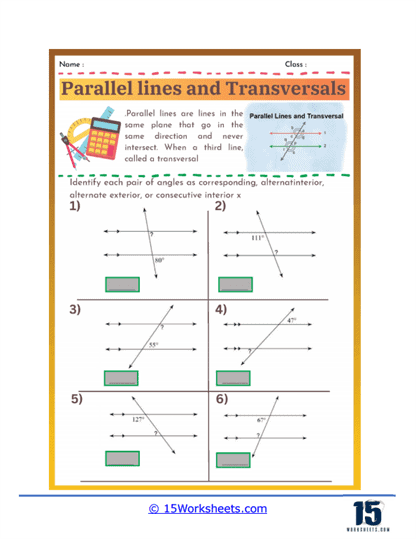
Corresponding Angles – These are pairs of angles that lie on the same side of the transversal and in corresponding positions. For example, one angle might be at the top left of one intersection and the other at the top left of the other intersection.
Alternate Interior Angles – These angles are on opposite sides of the transversal but inside the parallel lines.
Alternate Exterior Angles – These angles are on opposite sides of the transversal and outside the parallel lines.
Consecutive Interior Angles (Same-Side Interior Angles) – These angles are on the same side of the transversal and inside the parallel lines.
Using Geometric Theorems and Postulates
Corresponding Angles Postulate – States that if a transversal intersects two parallel lines, then each pair of corresponding angles is congruent.
Alternate Interior Angles Theorem – States that if a transversal intersects two parallel lines, then each pair of alternate interior angles is congruent.
Alternate Exterior Angles Theorem – States that if a transversal intersects two parallel lines, then each pair of alternate exterior angles is congruent.
Consecutive Interior Angles Theorem – States that if a transversal intersects two parallel lines, then each pair of consecutive interior angles is supplementary (sums to 180 degrees).
Solving for Unknown Angles
By understanding the key angle relationships formed when a transversal cuts through parallel lines, such as corresponding angles, alternate interior angles, and alternate exterior angles, which are all congruent, as well as consecutive interior angles, which are supplementary. By practicing these worksheets, students apply these relationships to identify and calculate unknown angles given one or more angle measures. The worksheets typically include diagrams that visually demonstrate these relationships, aiding in comprehension. Additionally, solving a variety of problems reinforces the concepts and helps students recognize patterns and develop problem-solving strategies. Through consistent practice, students build confidence in their ability to solve complex geometric problems involving parallel lines and transversals.
Types of Exercises On These Worksheets
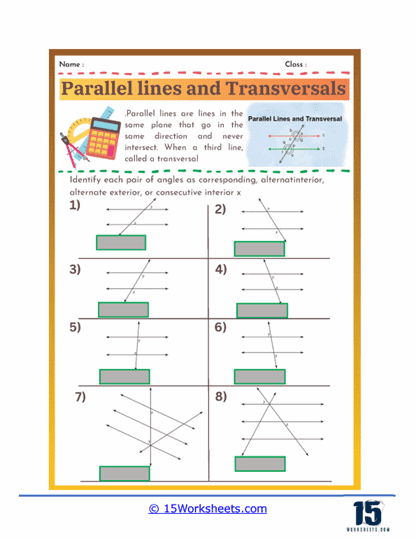
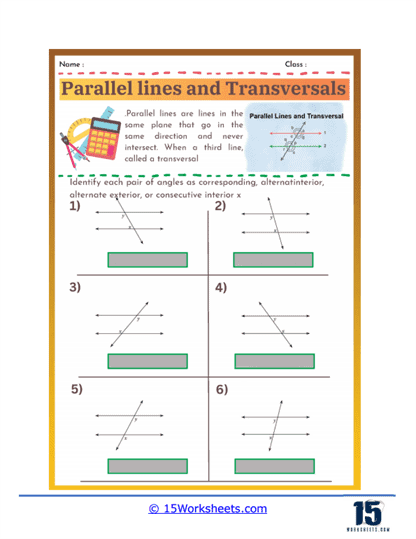
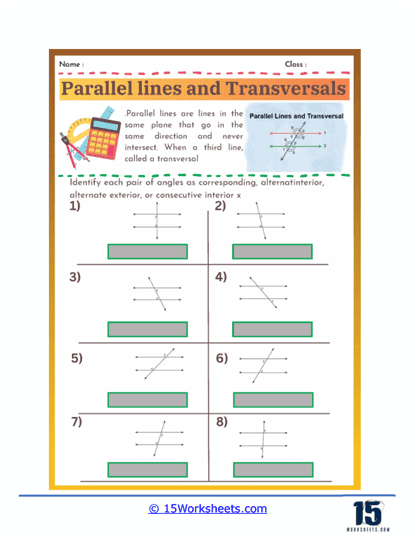
Identifying Angle Types
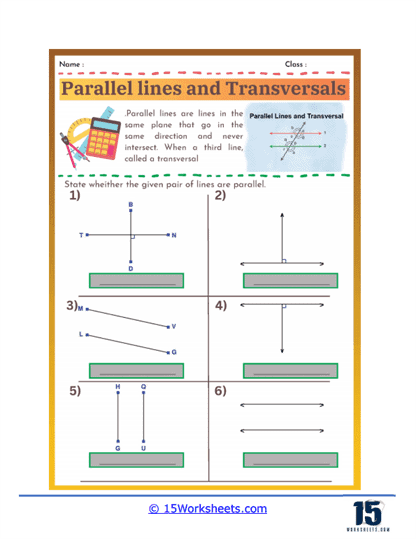
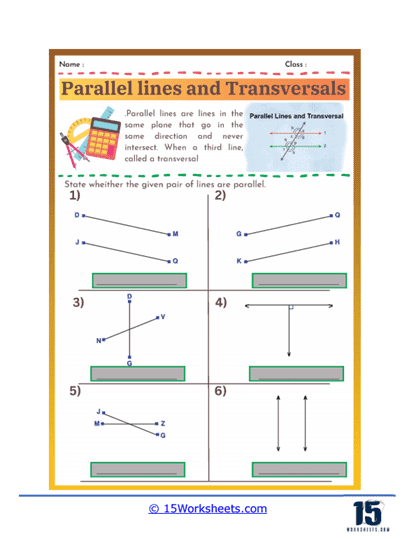
These problems present students with diagrams of parallel lines intersected by a transversal and ask them to identify specific angle types. Students need to recognize and label corresponding angles, alternate interior angles, alternate exterior angles, and consecutive (or same-side) interior angles. This type of problem helps students become familiar with the terminology and visual patterns associated with each angle type, laying the groundwork for more complex problem-solving.
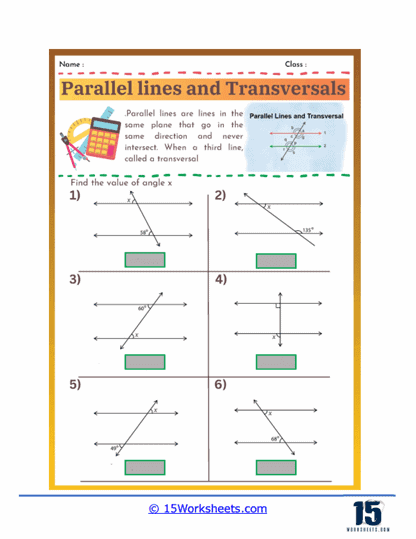
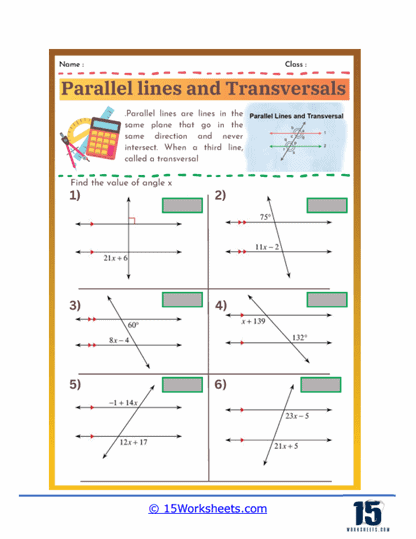
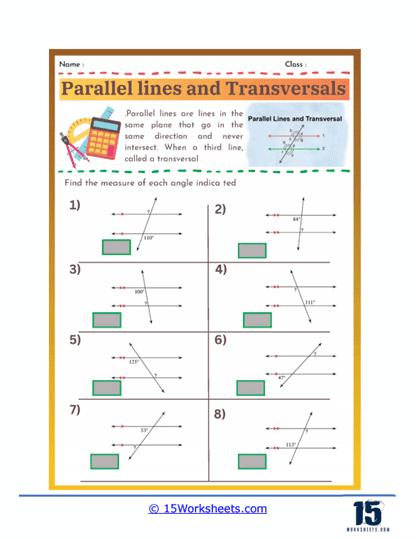
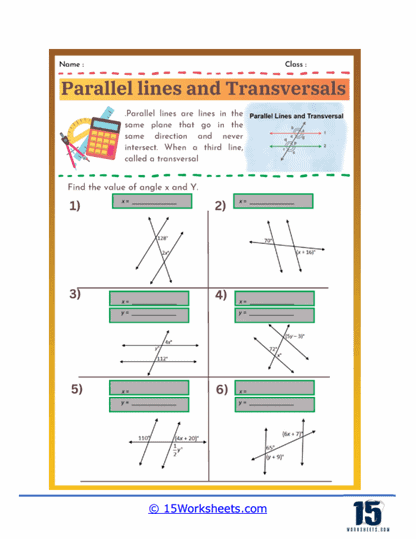
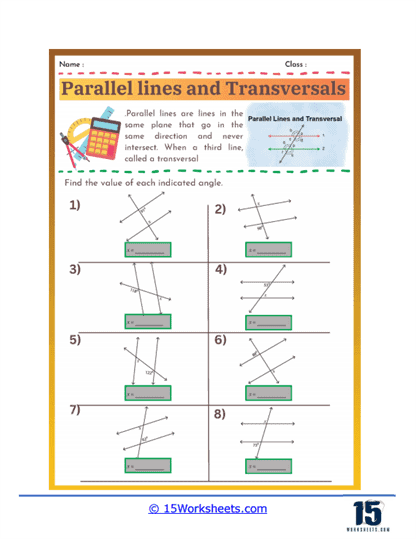
Calculating Unknown Angles
Students are given one or more angle measures in a diagram of parallel lines and a transversal and must use their knowledge of angle relationships to calculate the measures of unknown angles. These problems require students to apply properties such as the congruence of corresponding and alternate angles and the supplementary nature of consecutive interior angles. This type of exercise reinforces their understanding of these relationships and enhances their ability to use logical reasoning to find solutions.
Proof-Based Problems
Proof-based problems require students to write formal geometric proofs to demonstrate why certain angles are congruent or supplementary. Students must use axioms, definitions, and previously learned theorems to construct a logical argument. These problems develop students’ abilities to think critically and communicate their reasoning clearly, which are essential skills in both geometry and broader mathematical studies.
Real-World Application Problems
These problems present scenarios where students must apply their knowledge of parallel lines and transversals to solve real-world issues. Examples might include determining the angles of intersecting streets, the positioning of beams in construction, or angles of sunlight at different times of the day. These exercises show the practical relevance of geometric concepts and help students see the connection between theoretical knowledge and real-life applications.
Angle Relationships in Polygons
Students explore how parallel lines and transversals create angle relationships within various polygons, such as parallelograms and trapezoids. Problems might involve finding interior and exterior angles of these shapes by applying the properties of parallel lines and transversals. This type of problem helps students understand how these concepts extend beyond simple line diagrams to more complex geometric figures.
Angle Chasing
Angle chasing problems present a more complex diagram with multiple sets of parallel lines and transversals. Students must use a series of steps to determine unknown angles, often involving multiple angle relationships. These problems develop students’ abilities to follow a logical sequence of steps and use their geometric knowledge in a systematic way, enhancing their problem-solving skills.
Supplementary and Complementary Angles
These problems involve identifying pairs of supplementary (sum to 180 degrees) and complementary (sum to 90 degrees) angles formed by transversals cutting through parallel lines. Students use these relationships to find missing angle measures, reinforcing their understanding of these basic angle properties in the context of parallel lines and transversals.
Real-World Example
Consider an architect designing a building. The architect must ensure that the floors of the building are parallel to each other and that the walls intersect these floors at right angles. Understanding the geometric principles of parallel lines and transversals allows the architect to make precise calculations and ensure the structural integrity and aesthetic alignment of the building.
If the architect needs to determine the angle of a support beam intersecting parallel floors, they will use their knowledge of corresponding angles and alternate interior angles to make accurate measurements. This ensures that the support beams are installed correctly and contribute to the building’s stability.
Parallel lines and transversals worksheets are invaluable educational tools that help students develop essential geometric skills. Through a variety of exercises, students learn to identify and classify angles, apply geometric theorems, and solve for unknown angle measures. These worksheets provide a solid foundation in geometry, preparing students for advanced mathematical studies and real-world applications in fields such as architecture and engineering. By engaging with these worksheets, students enhance their analytical thinking and problem-solving abilities, making them well-equipped for future academic and professional challenges.