Graphing Circles Worksheets
About These 15 Worksheets
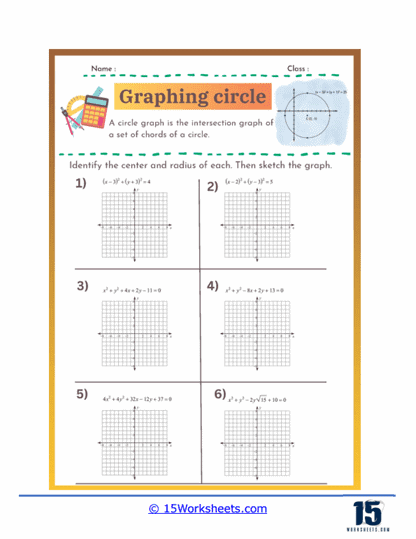
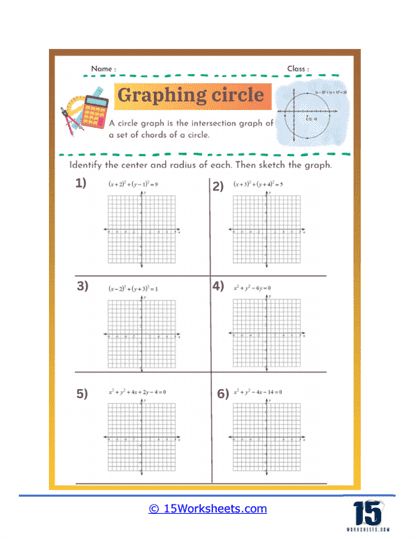
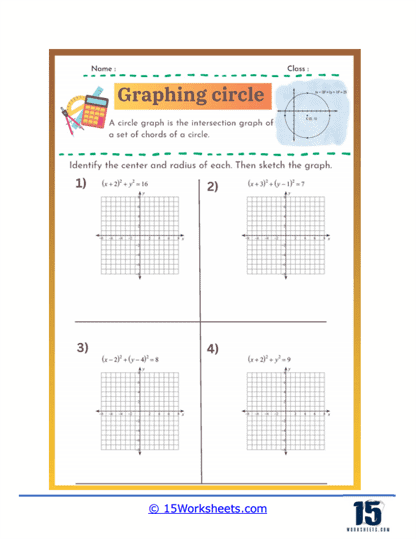
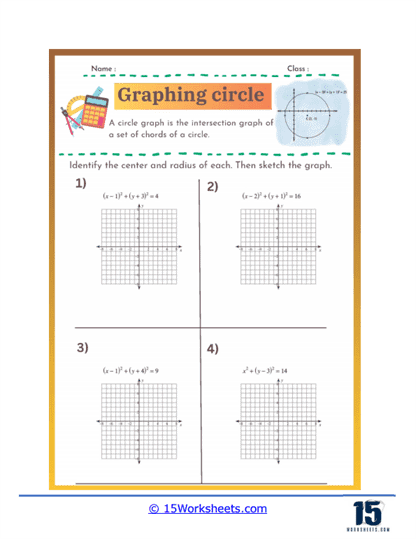
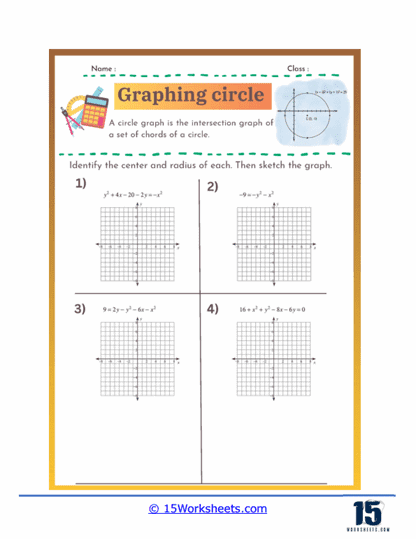
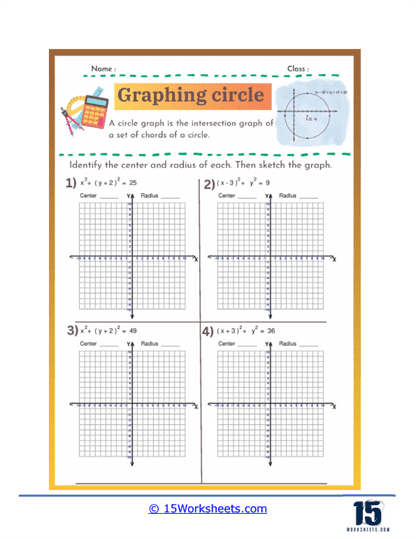
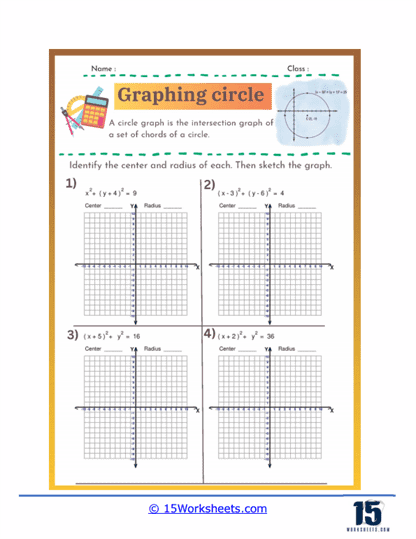
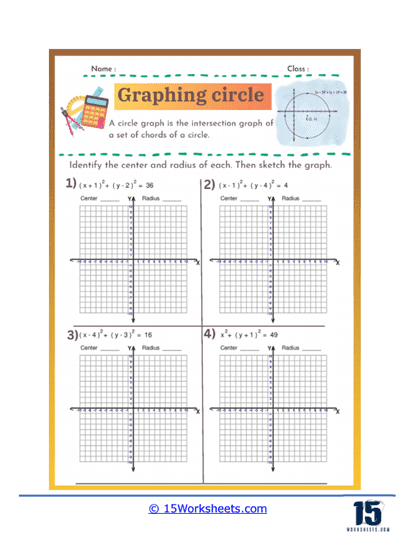
These worksheets were created to help students understand and practice the concepts related to circles in coordinate geometry. These worksheets guide students through the process of identifying the center and radius of a circle from its equation and graphing the circle on a coordinate plane. They are essential for reinforcing the geometric understanding of circles and the algebraic manipulations required to work with their equations. These worksheets are typically used in middle school and high school math classes to solidify students’ knowledge of circle equations, plotting points, and understanding geometric shapes.
Math Skills Explored
Understanding Circle Equations
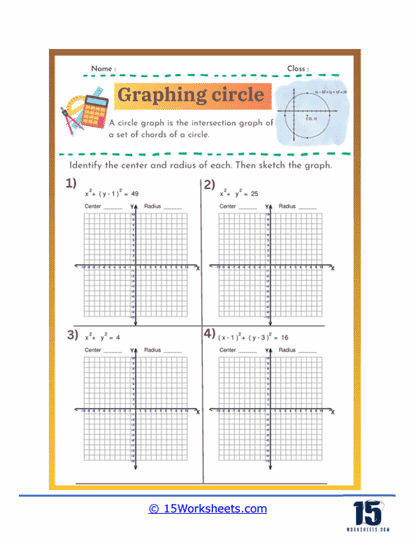
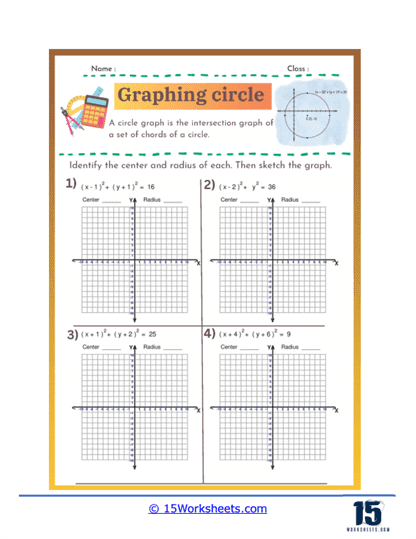
Graphing circles worksheets help students understand the standard equation of a circle and how to manipulate it. The standard form of a circle’s equation is (x – h)2 + (y – k)2 = r2. where (h, k) represents the circle’s center and r is the radius. These worksheets typically involve identifying the center and radius from the equation, as well as converting equations into standard form from other given formats. By practicing these skills, students develop a deeper understanding of the geometric properties of circles and how they are represented algebraically.
Plotting Points and Graphing
Graphing circles worksheets require students to plot points accurately on a coordinate plane, starting with the circle’s center and extending outward to define its radius. This exercise reinforces their ability to navigate and use the coordinate plane effectively. Additionally, students practice drawing the complete circle using the plotted points, which improves their precision and spatial awareness. This skill is fundamental not only in geometry but also in various applications of graphing in algebra and higher-level mathematics.
Solving Systems of Equations
Often, graphing circles worksheets include problems where students need to find the intersection points of a circle and a line or another circle. This requires solving systems of equations, where one equation represents the circle and the other represents the line or another circle. Students practice substituting and solving quadratic equations, reinforcing their algebraic manipulation skills and their understanding of how different geometric shapes interact on a coordinate plane.
Analyzing Graphs
Another key skill explored in these worksheets is analyzing and interpreting the graphs of circles. Students learn to recognize the effects of changing the radius or the center on the circle’s graph, enhancing their understanding of transformations in geometry. They also practice comparing different circles based on their equations and graphs, which helps in understanding concepts such as concentric circles and the relative positioning of multiple geometric figures. This analytical skill is crucial for more advanced studies in geometry and calculus, where interpreting graphs is a common task.
Types of Exercises
These worksheets offer a wide range of exercises and practice problems designed to reinforce different aspects of the concept of circles. Here are some common types of problems you might find:
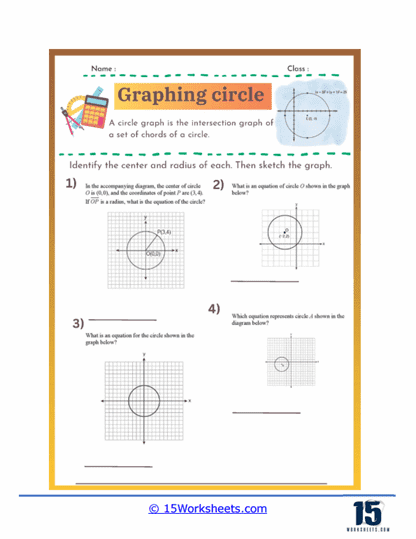
Identifying Center and Radius from Standard Form – These exercises provide the equation of a circle in its standard form and ask students to identify the center and radius. This type of problem helps students practice recognizing the components of the equation and understanding their geometric significance.
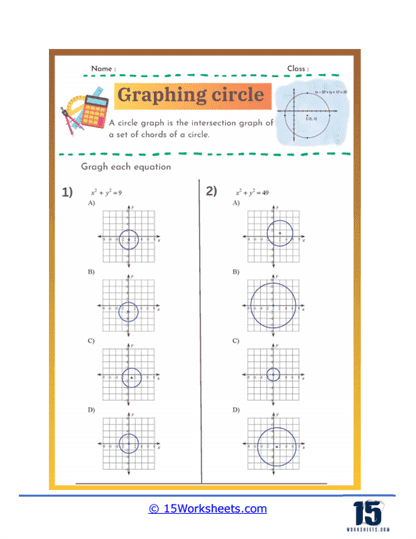
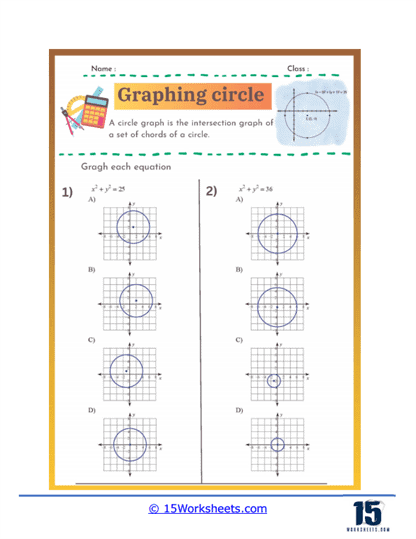
Graphing Circles – In these exercises, students are given the equation of a circle and must graph it on a coordinate plane. This type of problem reinforces their understanding of how the equation translates into a geometric shape.
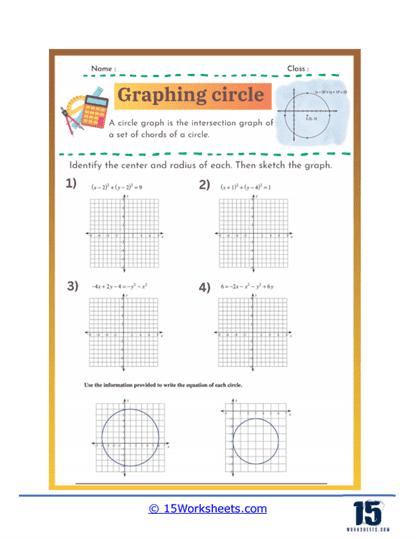
Converting General Form to Standard Form – These problems provide the equation of a circle in its general form and require students to convert it to the standard form. This helps students practice algebraic manipulation and understand the relationship between different forms of the equation.
Finding the Equation of a Circle from Geometric Information – In these exercises, students are given the center and radius of a circle or other geometric information, such as points on the circle or tangent lines, and must write the equation of the circle. This type of problem helps students practice translating geometric descriptions into algebraic equations.
Real-World Applications
These worksheets help students develop the skills necessary for various careers that involve the application of circle geometry. Understanding how to work with circles is crucial in numerous fields, and mastering these skills can open up exciting job opportunities. Here are some careers where knowledge of circle geometry plays a vital role:
Architecture and Urban Planning
Architects and urban planners use circle geometry regularly in their work. They design buildings, public spaces, and infrastructure, often incorporating circular elements such as fountains, roundabouts, and amphitheaters. Understanding how to graph and manipulate circles allows them to create aesthetically pleasing and functional designs. Architects need to calculate areas, perimeters, and distances to ensure their designs are both beautiful and practical. Accurate graphing ensures that the construction team can build the designs exactly as envisioned.
Engineering
Engineers, particularly civil and mechanical engineers, frequently use circle geometry in their projects. They design everything from bridges and tunnels to machinery and vehicles, often incorporating circular shapes and components. For instance, mechanical engineers might design gears, wheels, and rotating parts, all of which require precise calculations involving circles. Civil engineers might plan the layout of circular roundabouts or the curves of roads and highways. Mastery of circle equations and graphing is essential for creating efficient and safe designs.
Landscape Design
Landscape designers use circle geometry to plan gardens, parks, and outdoor spaces. They might design circular flower beds, pathways, and water features. Knowing how to accurately graph and calculate circles allows them to create harmonious and visually appealing landscapes. They need to understand the relationships between different circular elements and how they fit into the overall design of the space. Accurate calculations ensure that the landscape is not only beautiful but also functional and easy to maintain.
Astronomy
Astronomers and astrophysicists use circle geometry to study celestial bodies and their orbits. They analyze the paths of planets, moons, and satellites, which often involve circular or elliptical orbits. Understanding the equations of circles helps astronomers predict positions and movements in space. This knowledge is crucial for tasks such as launching satellites, planning space missions, and understanding the dynamics of planetary systems
Example Problem: Identify the center and radius of the circle given by the equation (x – 2)2 + (y + 3)2 = 25. Then sketch the graph of the circle.
Step-by-Step Solution
1. Identify the center of the circle
The equation of the circle is in the form
(x-h)2 + (y-k)2 = r2, where (h,k) is the center and r is the radius.
In this equation, h = 2 and k = -3.
Therefore, the center of the circle is (2,-3).
2. Determine the radius of the circle
The right side of the equation is 25, which represents 𝑟2.
To find the radius 𝑟, take the square root of 25.
𝑟 = 25 = 5.
3. Summarize the center and radius
Center: (2, -3)
Radius: 5
4. Sketch the graph of the circle
a. Plot the center of the circle at (2,-3) on the coordinate plane.
b. Use the radius of 5 to plot points that are 5 units away from the center in all directions (up, down, left, right).
c. Draw a smooth circle through these points.
Graph:
a. Center at (2,-3)
b. Radius of 5 units