Lines, Rays, Line Segments Worksheets
About These 15 Worksheets
These worksheets were developed to help students understand fundamental geometric concepts. These worksheets introduce and reinforce the definitions, properties, and differences between lines, rays, and line segments. Through a variety of exercises, students learn to identify and draw these geometric figures, enhancing their spatial reasoning and geometric understanding. The worksheets cater to various learning styles by combining textual explanations, visual diagrams, and practical exercises.
Lines
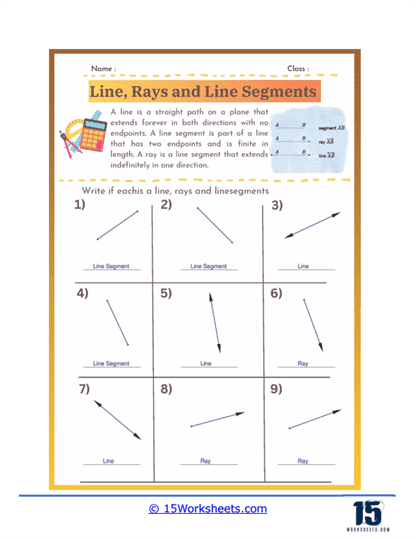
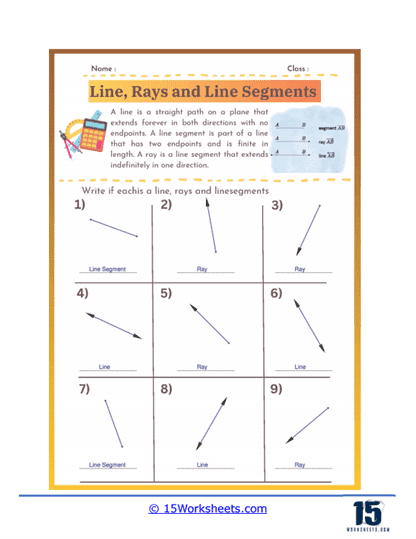
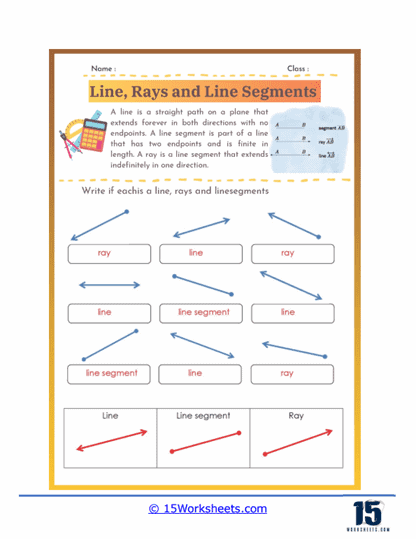
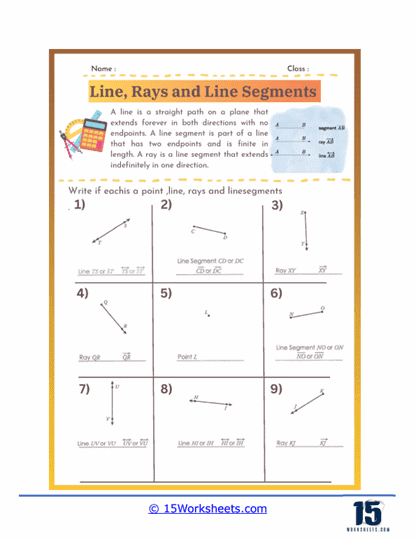
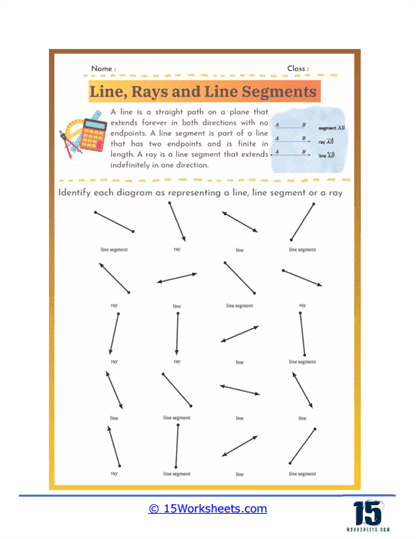
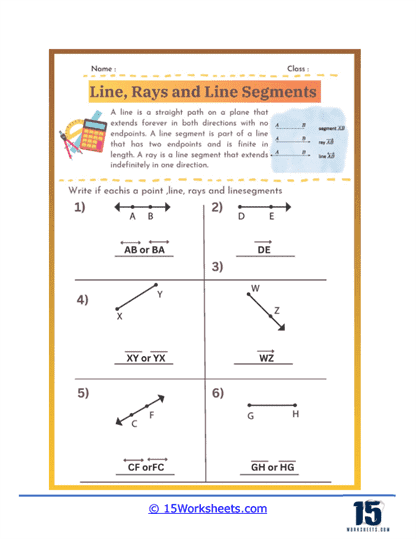
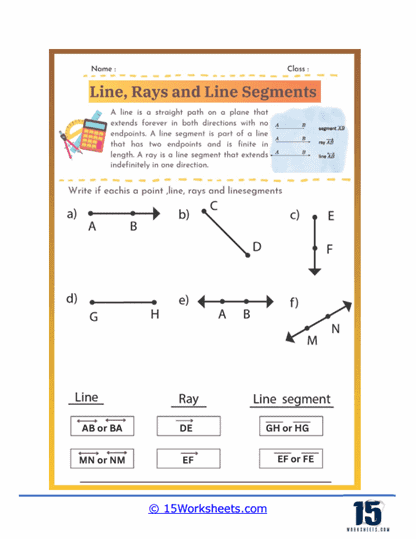
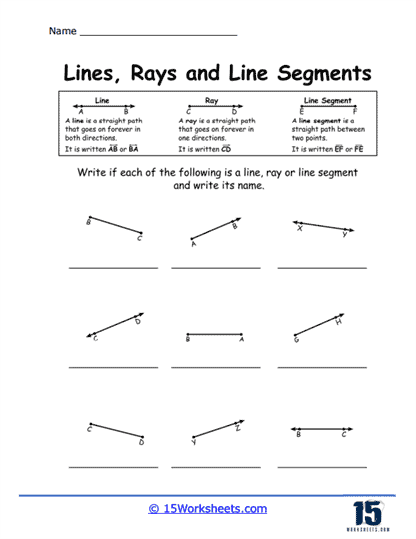
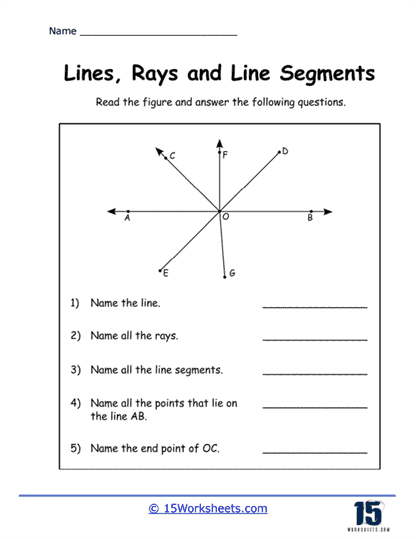
A line is a fundamental concept in geometry that represents a straight, one-dimensional figure extending infinitely in both directions. It is defined by any two points along its length, and is often denoted with a lowercase letter or by naming two points on the line with a double-headed arrow above the points. Lines have no endpoints and no fixed length, which distinguishes them from line segments and rays. They are essential in geometry for defining shapes, angles, and for describing the relationships between different geometric figures.
Rays
A ray is a part of a line that starts at a specific point, called the endpoint, and extends infinitely in one direction. It is represented by naming its endpoint first, followed by another point on the ray, with a single-headed arrow above the points indicating the direction. Rays are used in geometry to describe paths that have a starting point but no end, such as the direction of a light beam or the side of an angle. Unlike lines, rays have a defined starting point but continue indefinitely in one direction.
Line Segments
A line segment is a part of a line that is bounded by two distinct endpoints. It has a definite length, which can be measured, and is represented by naming its endpoints with a line above the points. Line segments are fundamental in defining the sides of polygons and other geometric shapes. Unlike lines and rays, line segments do not extend infinitely; they are finite and can be measured. They are crucial for constructing shapes, determining distances, and for various applications in both theoretical and applied geometry.
Explored Math Skills
Understanding Basic Geometric Concepts
Lines, rays, and segments worksheets help students grasp fundamental geometric concepts. These worksheets introduce students to the basic definitions and properties of lines, rays, and line segments. They provide exercises where students learn to differentiate between these geometric figures based on their characteristics, such as endpoints and directionality. This foundational knowledge is crucial for progressing to more complex geometric topics.
Plotting and Identifying Points
One of the key skills explored in these worksheets is the ability to plot and identify points on a coordinate plane. Students practice marking points that define lines, rays, and segments, reinforcing their understanding of the Cartesian coordinate system. This skill is essential for accurately drawing and interpreting geometric figures and for understanding the spatial relationships between different points.
Drawing and Measuring
Lines, rays, and segments worksheets often involve drawing these figures accurately. Students use rulers and protractors to measure and draw line segments to a specified length and to create rays and lines with precision. These exercises help students develop their skills in measurement and drawing, which are important for both geometry and practical applications like technical drawing and design.
Understanding and Applying Geometric Notation
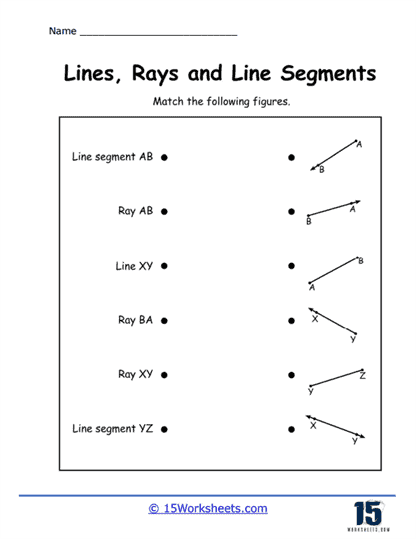
These worksheets teach students the correct notation for lines, rays, and line segments. For example, students learn to use symbols like ↔ for lines, __ for line segments. Understanding and using this notation correctly is crucial for clear communication in geometry. It also prepares students for advanced mathematical writing and problem-solving.
Analyzing Geometric Relationships
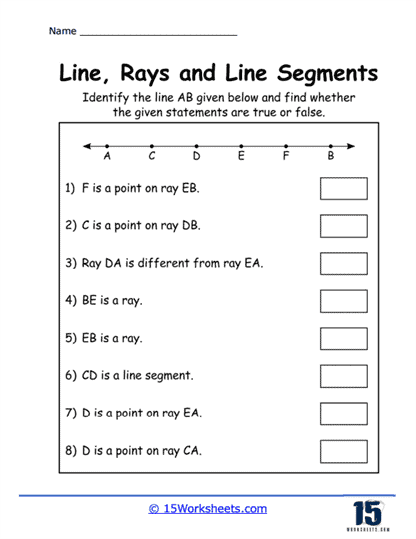
Worksheets on lines, rays, and segments often include problems that require students to analyze geometric relationships. For example, students might need to determine whether two lines are parallel or perpendicular, identify the intersection point of two lines, or understand the relationships between different segments within a polygon. These exercises enhance students’ analytical skills and their ability to reason logically about geometric relationships.
Solving Real-World Problems
Many worksheets incorporate real-world scenarios where students apply their knowledge of lines, rays, and segments. For example, they might need to find the shortest path between two points, understand the concept of line of sight, or determine the direction of a beam of light. These practical applications show students the relevance of geometry in everyday life and help them develop problem-solving skills that can be applied outside the classroom.
Calculating Distances
Another important skill explored in these worksheets is calculating the distance between points, particularly for line segments. Students practice using the distance formula. This exercise helps students understand how to calculate precise measurements in a coordinate plane, which is crucial for various applications in science, engineering, and everyday tasks that require precise measurements.
Understanding Segment Addition and Midpoints
Worksheets on lines, rays, and segments often include problems involving segment addition and midpoints. Students learn how to find the midpoint of a segment using the midpoint formula. They also practice adding segment lengths to find the total length of a composite segment. These exercises reinforce their understanding of arithmetic operations and their ability to manipulate and understand geometric figures.
Types of Exercises
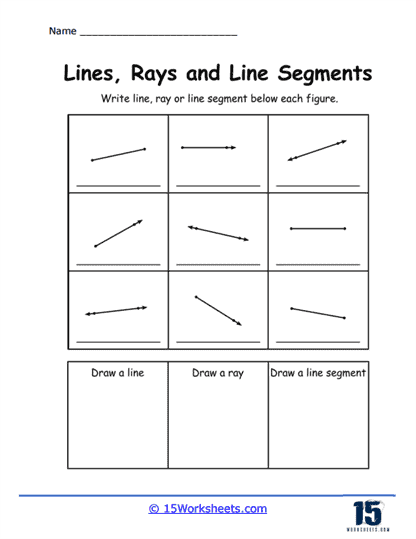
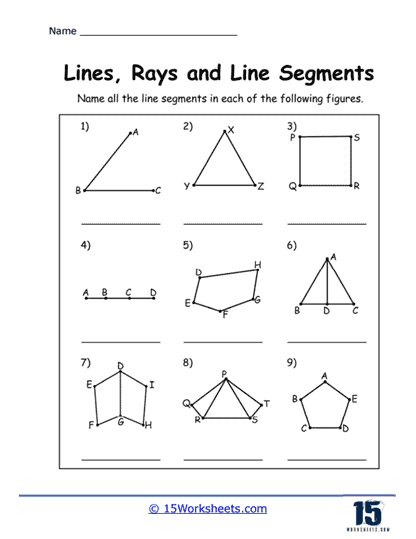
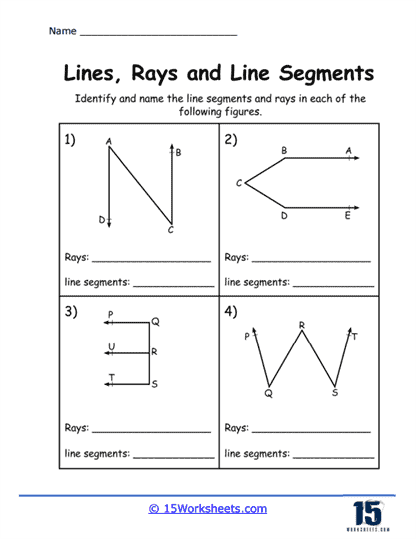
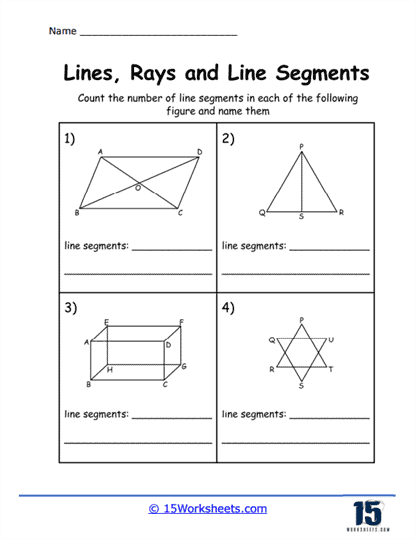
Identifying Lines, Rays, and Segments – In this type of problem, students are given several figures and must identify each one as a line, ray, or segment. These exercises help students understand the fundamental properties of each figure, such as the presence of endpoints and directionality. This type of problem reinforces their ability to distinguish between these basic geometric constructs.
Drawing Lines, Rays, and Segments – Students are tasked with drawing lines, rays, and segments based on given instructions. This helps them practice precision in creating geometric figures and ensures they understand how to represent each type correctly. These problems enhance their spatial awareness and ability to follow geometric instructions accurately.
Plotting Points on a Coordinate Plane – These problems involve placing specific points on a coordinate plane to form lines, rays, or segments. Students practice using the Cartesian coordinate system, which is crucial for understanding spatial relationships and for solving more complex geometric problems. Plotting points helps solidify their skills in graphing and interpreting geometric figures.
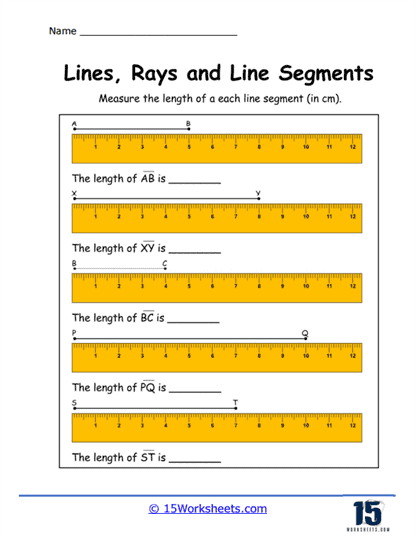
Measuring Line Segments – Students are asked to measure the length of given line segments using rulers or scales. This type of problem emphasizes accuracy in measurement and understanding the concept of length in a geometric context. It is essential for developing practical skills in both geometry and real-world applications.
Identifying Relationships Between Figures – Problems in this category require students to analyze the relationships between lines, rays, and segments, such as determining if they are parallel, perpendicular, or intersecting. These exercises develop their analytical skills and their ability to reason about geometric relationships. Understanding these relationships is key for more advanced geometric concepts.
Finding Midpoints and Endpoints – In these problems, students find the midpoint of a line segment or determine the coordinates of an endpoint given the midpoint and one endpoint. This reinforces their understanding of symmetry and division in geometry. It also helps them apply their knowledge of geometric properties to solve problems involving distance and positioning.
Segment Addition Problems – Students are given composite segments and must determine the total length by adding the lengths of individual segments. These problems help students understand the concept of adding lengths and the properties of line segments. They are essential for building skills in both arithmetic and geometry.
Real-World Application Problems – These problems present scenarios where students must apply their knowledge of lines, rays, and segments to solve practical issues, such as finding the shortest path or determining visibility. They help students see the relevance of geometric concepts in everyday life and develop problem-solving skills. This type of problem bridges the gap between theoretical geometry and real-world applications.
Comparing Lengths and Angles – Students compare the lengths of line segments or the angles formed by rays to determine which is longer or greater. These exercises help them develop an intuitive sense of measurement and comparison in geometry. They also reinforce the importance of precision and accuracy in geometric reasoning.
Transformations – In these problems, students apply transformations such as translations, reflections, and rotations to lines, rays, and segments. This helps them understand how geometric figures change under different transformations while maintaining their fundamental properties. These exercises are crucial for understanding more advanced concepts in geometry, such as symmetry and congruence.
Benefits of These Worksheets
Foundational Understanding of Geometry
Using lines, rays, and segments worksheets provides students with a solid foundation in geometry. These worksheets introduce basic geometric concepts and help students differentiate between different types of geometric figures. By working through these exercises, students gain a clear understanding of how lines extend infinitely, how rays have a single endpoint and extend in one direction, and how segments have two endpoints and a finite length. This foundational knowledge is crucial as it sets the stage for more complex geometric studies and applications.
Development of Precision and Accuracy
One of the key benefits of lines, rays, and segments worksheets is the development of precision and accuracy in students’ work. These worksheets often require students to draw geometric figures accurately using rulers and other tools, enhancing their ability to create precise drawings. Measuring line segments and plotting points on a coordinate plane further reinforce the importance of accuracy. These skills are not only essential for success in geometry but are also applicable in various fields that require meticulous attention to detail, such as engineering, architecture, and technical drawing.
Enhancement of Analytical and Problem-Solving Skills
Lines, rays, and segments worksheets are designed to improve students’ analytical and problem-solving skills. By engaging in exercises that require them to identify geometric relationships, such as determining if lines are parallel, perpendicular, or intersecting, students develop their ability to think critically and reason logically. These problems often involve multiple steps and require students to apply various geometric principles, fostering a deeper understanding of the subject. This analytical thinking is beneficial beyond geometry, as it is a crucial skill in many academic and professional disciplines.
Application of Mathematical Notation
Learning to use and understand geometric notation is another significant benefit of these worksheets. Students become familiar with the correct symbols for lines, rays, and segments, and practice writing and interpreting these notations accurately. This knowledge is essential for clear communication in geometry and is a skill that will be useful in higher-level mathematics and related fields. Proper use of mathematical notation also helps students when they need to write proofs or explain their reasoning in a clear and concise manner.
Real-World Relevance
Lines, rays, and segments worksheets often include real-world application problems, which help students see the practical relevance of geometry in everyday life. These problems might involve finding the shortest path, understanding sightlines, or solving issues related to design and construction. By applying geometric concepts to real-world scenarios, students appreciate the value of what they are learning and are more motivated to engage with the material. This practical application of geometric principles prepares students for real-life problem-solving and decision-making.