Reflection, Rotation, Translation Worksheets
About These 15 Worksheets
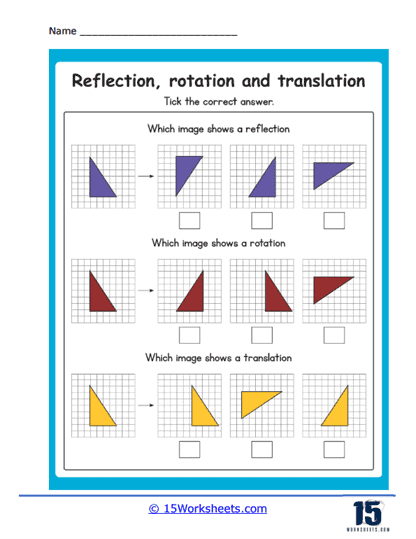
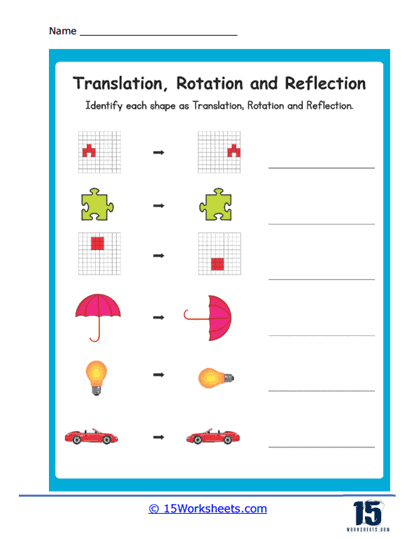
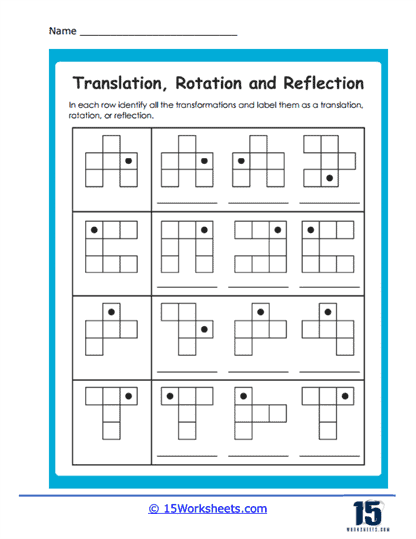
These worksheets were made to help students understand and practice geometric transformations. These worksheets focus on three main types of transformations – reflection (flipping a shape over a line), rotation (turning a shape around a point), and translation (sliding a shape from one position to another). By engaging with these worksheets, students can visualize and comprehend how shapes change their positions and orientations in a coordinate plane without altering their size or shape.
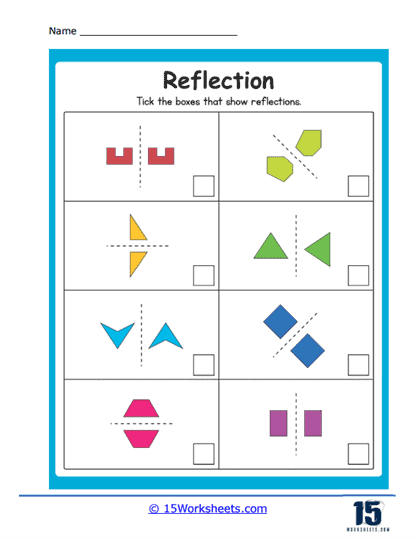
Understanding Reflection
Reflection involves flipping a shape over a specified line, creating a mirror image. In these worksheets, students typically encounter problems where they must reflect shapes across horizontal, vertical, or diagonal lines. The exercises often begin with simple shapes like triangles, squares, or letters, gradually progressing to more complex figures. By drawing the reflected image, students learn to identify the symmetry and the precise positioning of points relative to the reflection line.
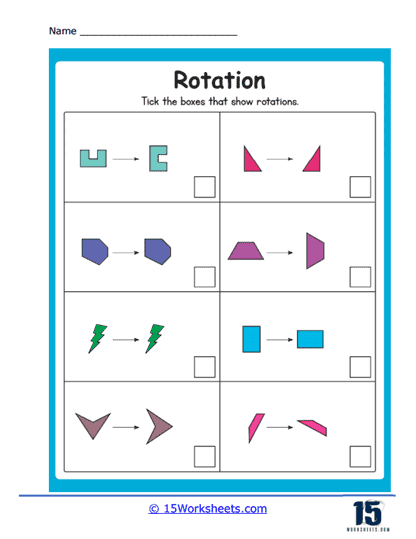
Exploring Rotation
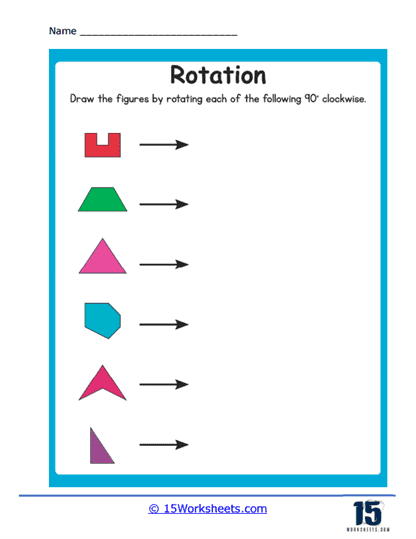
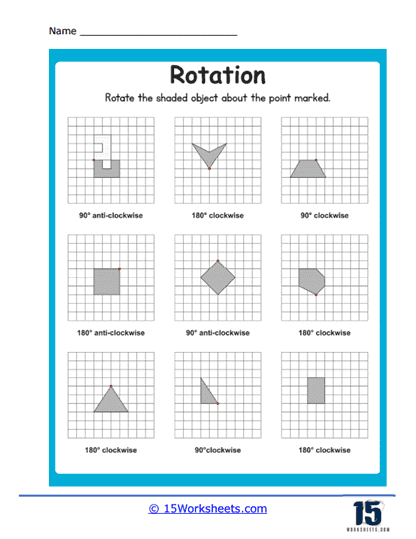
Rotation involves turning a shape around a fixed point by a specified angle, either clockwise or counterclockwise. These worksheets help students understand the concept of rotational symmetry and how shapes maintain their properties while changing orientation. Exercises might ask students to rotate shapes by 90 degrees, 180 degrees, or 270 degrees around a given point.
In one example, a worksheet might show a square centered at (2,2) and ask students to rotate it 90 degrees clockwise around the origin. Students would need to calculate the new coordinates of each vertex and redraw the square in its new orientation.
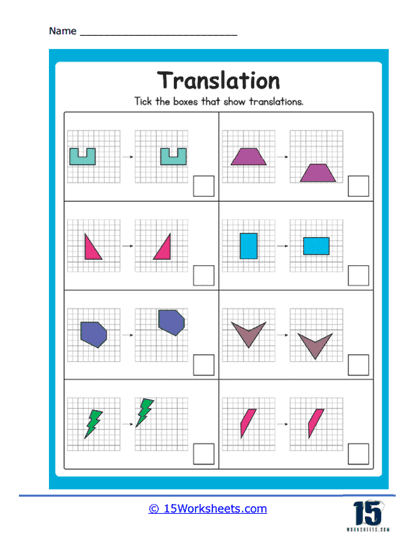
Practicing Translation
Translation is the process of moving a shape from one location to another on a grid without changing its orientation or size. Translation exercises on these worksheets require students to shift shapes by a specified number of units horizontally and vertically. These problems help students develop a strong sense of spatial awareness and the ability to visualize movements in a coordinate plane.
Types of Reflection Problems
Identifying Reflected Images – These problems present a shape and a line of reflection, asking students to draw the reflected image. Students must understand that each point on the shape is mirrored across the line of reflection at an equal distance.
Describing Reflections – Students are given a shape and its reflected image and must describe the line of reflection. These problems require them to analyze the symmetry and determine where the line of reflection lies.
Coordinate Reflections – These problems involve reflecting points or shapes across a given line in the coordinate plane, such as the x-axis or y-axis. Students practice determining the new coordinates of the reflected points.
Complex Reflections – Students might be asked to reflect shapes across lines that are not the x- or y-axis, such as y = x or y = -x. This type of problem requires a deeper understanding of reflection rules and coordinate transformations.
Types of Rotation Problems
Identifying Rotated Images – These problems provide a shape and a center of rotation, asking students to draw the shape after a specified rotation, such as 90°, 180°, or 270°. Students must visualize how the shape turns around the center.
Describing Rotations – Given a shape and its rotated image, students must describe the angle and direction of rotation, identifying the center of rotation as well. This involves understanding rotational symmetry and geometric relationships.
Coordinate Rotations – Students rotate points or shapes around the origin or another specified point in the coordinate plane. They need to determine the new coordinates after the rotation.
Complex Rotations – Problems may involve rotating shapes by angles that are not multiples of 90°, requiring students to apply trigonometric reasoning or more advanced rotational techniques.
Types of Translation Problems
Identifying Translated Images – Students are given a shape and asked to draw the image after it has been translated a certain distance in a specified direction (e.g., 5 units right and 3 units up). They must accurately shift the entire shape based on the given translation vector.
Describing Translations – Given a shape and its translated image, students must describe the translation vector that maps the original shape to its new position. This helps them understand the concept of vector addition.
Coordinate Translations – These problems involve translating points or shapes in the coordinate plane by adding or subtracting the translation vector to the coordinates of the points.
Complex Translations – Problems may combine translations with other transformations, requiring students to apply multiple steps to find the final position of a shape.
Benefits of These Worksheets
Enhancing Spatial Reasoning and Visualization Skills
Working with reflection, rotation, and translation worksheets significantly enhances students’ spatial reasoning and visualization skills. These worksheets require students to mentally manipulate shapes and figures, helping them to better understand how objects move and change in space. By practicing these transformations, students develop the ability to visualize geometric operations and their effects, which is crucial for solving complex problems in geometry and other fields that involve spatial reasoning.
Understanding Geometric Transformations
These worksheets provide a hands-on approach to understanding geometric transformations, which are foundational concepts in geometry. Reflection involves flipping a shape over a line to create a mirror image, rotation involves turning a shape around a fixed point, and translation involves sliding a shape from one position to another without changing its orientation. By working through these exercises, students learn the properties and rules of each transformation, deepening their comprehension of how shapes can be manipulated while preserving their fundamental characteristics.
Reinforcing Mathematical Rigor and Precision
Reflection, rotation, and translation worksheets require students to apply precise mathematical rules and procedures. For instance, they must accurately measure angles and distances to perform rotations and translations, and use coordinate pairs to map reflections. This precision helps reinforce mathematical rigor, as students must carefully follow steps and check their work to ensure accuracy. Developing this attention to detail is valuable for higher-level mathematics and technical fields where precision is paramount.
Building Problem-Solving Skills
These worksheets present various challenges that enhance students’ problem-solving skills. Each transformation type requires a different approach and set of strategies, encouraging students to think critically and creatively. For example, determining the correct angle and direction for a rotation or the line of reflection for a mirror image involves analytical thinking and systematic problem-solving. These skills are transferable to many areas of study and real-world situations, where complex problems often require innovative solutions.
Application to Real-World Contexts
Understanding reflections, rotations, and translations has practical applications in the real world. These transformations are used in various fields such as computer graphics, engineering, architecture, and even in everyday tasks like navigating maps or arranging furniture. By working with these worksheets, students see the relevance of geometric transformations in real-life contexts, which can increase their interest and motivation in learning geometry.
Enhancing Understanding of Symmetry and Patterns
Worksheets on reflections, rotations, and translations help students recognize and understand symmetry and patterns in shapes and designs. Symmetry is a fundamental concept in many areas of mathematics and the natural world. By exploring how shapes can be transformed to create symmetrical patterns, students develop a deeper appreciation for the aesthetic and structural aspects of symmetry. This understanding is particularly useful in art, design, and architecture.
Preparing for Advanced Studies
Mastering geometric transformations prepares students for more advanced studies in mathematics and related disciplines. Concepts like congruence, similarity, and coordinate geometry all build on an understanding of transformations. For students pursuing STEM fields, this knowledge is essential for subjects such as physics, computer science, and engineering. These worksheets lay the groundwork for understanding more complex mathematical theories and applications.
Promoting Active Learning and Engagement
Reflection, rotation, and translation worksheets often involve interactive and hands-on activities, which promote active learning and engagement. Students might use graph paper, drawing tools, or software to perform transformations, making the learning process dynamic and engaging. This active involvement helps students retain information better and fosters a more enjoyable learning experience.
Improving Coordination and Fine Motor Skills
When students use tools like compasses, protractors, and rulers to perform transformations, they also improve their coordination and fine motor skills. These practical skills are important for tasks that require precision and control, such as technical drawing, drafting, and various hands-on professions. Developing these skills through geometry worksheets provides a well-rounded educational experience.
Encouraging Collaborative Learning
These worksheets can also be used in group activities, encouraging collaborative learning. Students can work together to solve transformation problems, discuss strategies, and share insights. This collaboration fosters communication skills, teamwork, and the ability to learn from others, which are important competencies in both academic and professional environments.