Graphing Lines Worksheets
About These 15 Worksheets
Graphing Lines Worksheets are educational tools designed to help middle school students understand and master the concept of graphing lines on a coordinate plane. These worksheets typically contain a variety of exercises that build on each other, starting from the fundamental principles of graphing lines and progressively incorporating more complex elements.
The basic idea behind graphing lines is that you’re taking an equation, like y = 2x + 3, and drawing it on a coordinate plane. This graph visually represents all possible solutions to the equation. The coordinate plane, as you may already know, is a two-dimensional space defined by a horizontal axis (x-axis) and a vertical axis (y-axis). A line graphed on this plane provides a visual representation of a relationship between two variables – the x (independent variable) and y (dependent variable).
The Types of Exercises on These Worksheets
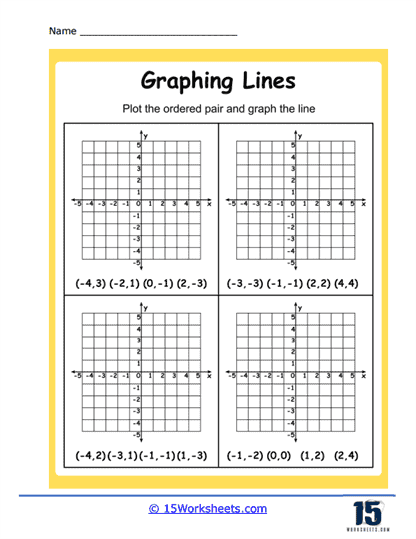
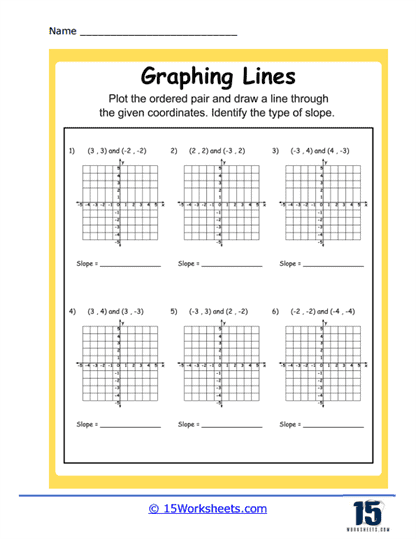
1. Plotting Points and Drawing Lines – These are typically the first exercises you’ll encounter. Here, you’re given a series of ordered pairs, or coordinates, to plot on a coordinate plane. After plotting these points, you’ll connect them to form a line. This helps you understand how lines are represented on a coordinate plane.
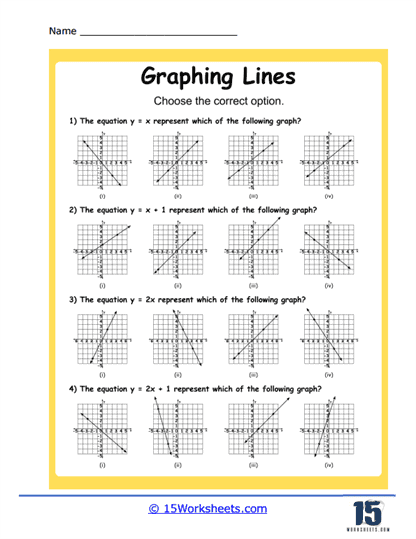
2. Graphing Lines from Equations – In this type of exercise, you’re given a linear equation (such as y = 2x + 3) and asked to graph it. To do this, you might select a few values for x, calculate the corresponding y-values, and then plot these points on the plane. You can then draw a line through the points. These exercises help you understand how to translate an equation into a visual representation.
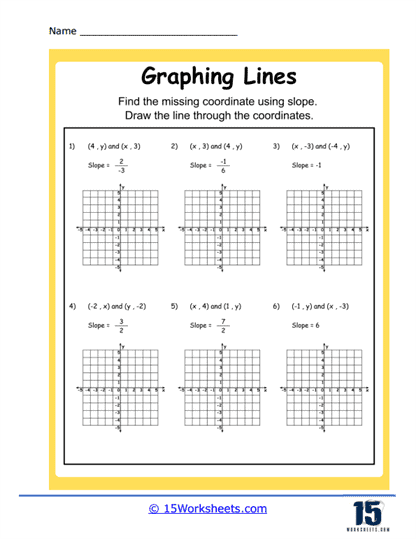
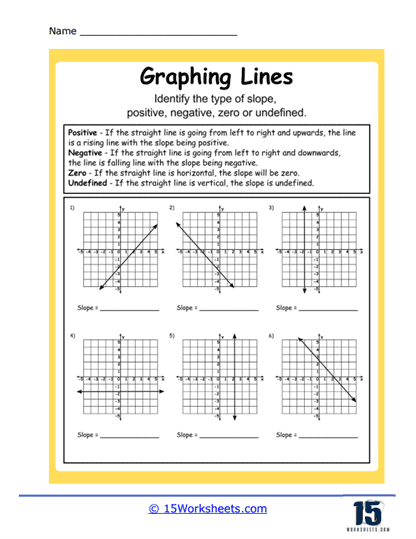
3. Determining Slope and Y-Intercept – This type of exercise involves identifying the slope and y-intercept from a given equation and using these to graph the line. The slope, represented by ‘m’ in the equation y = mx + b, tells you how steep the line is, while the y-intercept ‘b’ tells you where the line crosses the y-axis.
4. Graphing from Slope-Intercept Form – These exercises provide equations in slope-intercept form (y = mx + b) and ask you to graph the line. This not only solidifies your understanding of slope and y-intercept but also lets you practice creating graphs from these forms of equations.
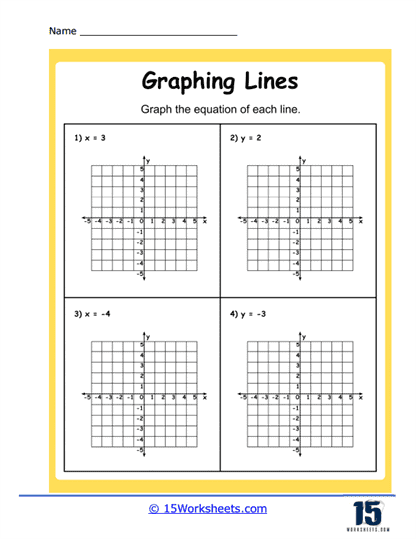
5. Graphing Horizontal and Vertical Lines – In these exercises, you’ll graph horizontal and vertical lines, which have equations like x = 4 or y = -2. This helps you understand how these special types of lines relate to the coordinate plane and how their equations differ from the standard y = mx + b format.
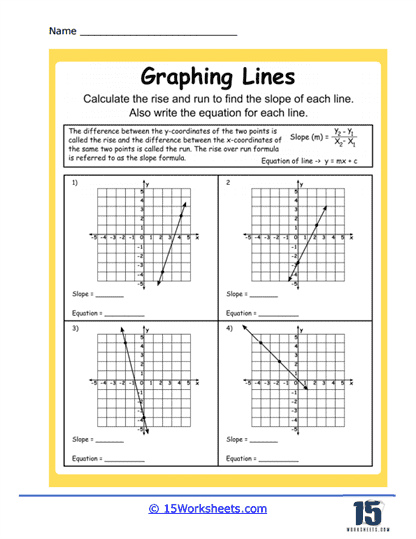
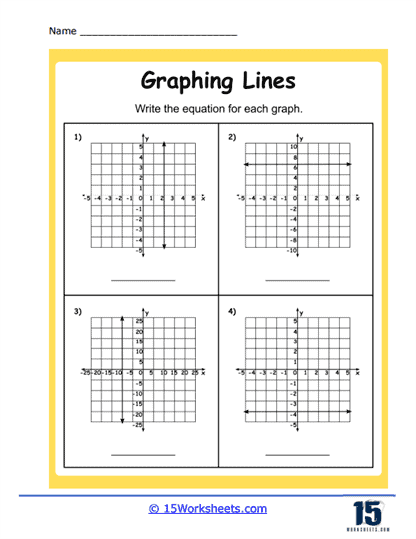
6. Interpreting Graphs – These exercises involve already-plotted lines, and your task is to interpret the graph. You might be asked to determine the slope and y-intercept of the line, write the equation of the line, or describe what the line represents in a given context.
7. Problem-Solving Exercises – In these exercises, you might be given a word problem that involves a real-life situation, like tracking a car’s distance over time. You’ll need to formulate a linear equation representing the scenario, then graph the line.
What Are the Benefits Of These Worksheets
By regularly practicing on Graphing Lines Worksheets, you gain a deeper understanding of the relationships between equations and their corresponding lines. You’ll learn how to visualize abstract mathematical concepts, which is a critical step in understanding and solving more complex problems in algebra and geometry.
Graphing lines helps you understand the concept of slope and y-intercept. Recognizing how these two parameters affect a line’s orientation on the coordinate plane is an essential skill in mathematics. It aids you in interpreting the rate of change and initial value in real-world scenarios, like understanding the speed of a moving object (slope) or the starting point of a process (y-intercept).
These worksheets also enhance your data interpretation skills. The ability to read, interpret, and analyze graphical data is crucial in many fields, including science, business, and social studies. By interpreting the line graphs, you can identify trends, make predictions, and draw conclusions about the data.
How to Graph a Linear Equation
Graphing a linear equation can seem like a daunting task if you’re not familiar with the process, but once you understand the steps involved, it becomes straightforward. Let’s break it down.
A linear equation is an equation between two variables that produces a straight line when graphed. These equations are typically written in the form y = mx + b, where m represents the slope of the line and b is the y-intercept. Here’s a step-by-step guide on how to graph a linear equation:
1. Identify the Slope and the y-intercept – Start by rewriting your equation in slope-intercept form (y = mx + b) if it’s not already in that form. In this form, m is the slope of the line, and b is the y-intercept.
For example, in the equation y = 2x – 3, the slope (m) is 2, and the y-intercept (b) is -3.
2. Plot the y-intercept – The y-intercept is the point where the line crosses the y-axis. This is always the point (0,b). Start by finding the y-intercept on your graph and make a point at this location.
In our example, the y-intercept is -3. So, plot a point at (0, -3).
3. Use the Slope to Plot the Next Point – The slope is a measure of the steepness of the line and is defined as the ratio of the vertical change (the rise) to the horizontal change (the run). If the slope is positive, the line rises from left to right, and if it’s negative, it falls from left to right. If the slope is 2, for example, this means you go up 2 units (rise) for every 1 unit you go to the right (run).
In our example, the slope is 2. Starting from the y-intercept, count 2 units up (rise of 2) and 1 unit to the right (run of 1), and then make a point there.
4. Draw the Line – Once you have at least two points, you can draw a line that passes through them. This line is the graph of your linear equation. You can extend the line as far as you want in both directions, but be sure to draw arrows on the ends of the line to indicate it extends indefinitely.
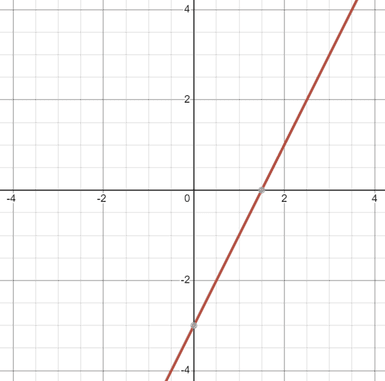
In our example, you should have a line passing through the points (0, -3) and (1, -1).
Remember to label your graph, indicating the equation of the line, and the x and y axes.
Understanding how to graph a linear equation is a fundamental skill in algebra. It helps you visualize the solutions to the equation and the relationship between the variables. Additionally, it aids in understanding more complex mathematical concepts like systems of equations and inequalities.
Real-life applications of graphing linear equations are abundant in various fields such as physics, economics, and engineering. For instance, businesses often use linear equations to predict future sales based on past data, and engineers use them to model and solve problems involving constant rates of change.
By learning to graph a linear equation, you’re not only gaining a key mathematical skill but also equipping yourself with a tool that can help solve real-world problems and make informed decisions based on trends and predictions.