Measuring Angles Worksheets
About These 15 Worksheets
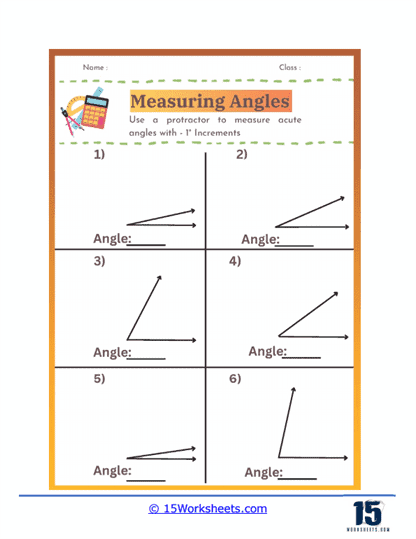
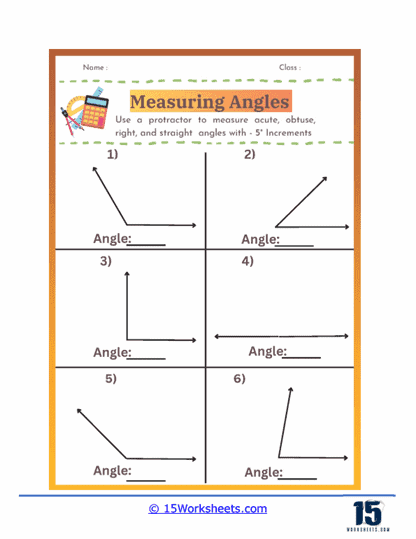
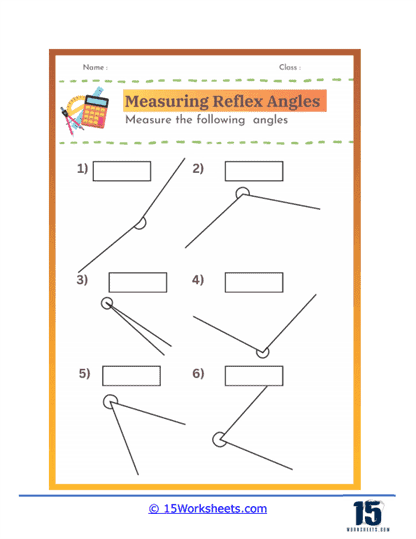
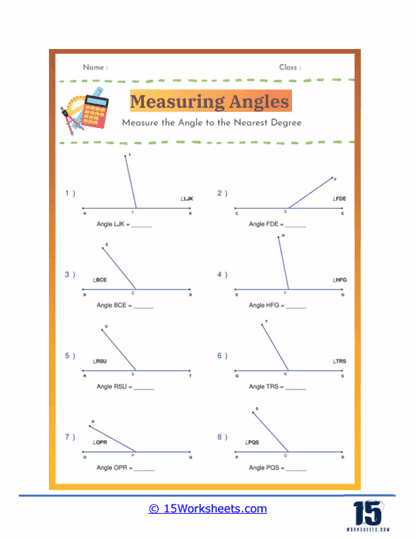
These worksheets will help students practice and master the skill of measuring angles using a protractor. These worksheets present various types of angles, ranging from acute to obtuse, and require students to measure and record the angles accurately. By engaging with these worksheets, students enhance their understanding of geometric concepts and improve their ability to use a protractor effectively.
These worksheets typically include a variety of angles presented in different orientations, ensuring that students become comfortable with measuring angles regardless of their position on the page. The primary focus is on developing students’ proficiency in identifying the degrees of angles and understanding the relationships between different types of angles. As students work through these exercises, they gain a deeper comprehension of geometry and its practical applications.
Math Skills Explored
Measuring Angles worksheets explore several critical math skills that are essential for students’ overall mathematical development. These skills include:
Protractor Usage – Students learn how to use a protractor to measure angles accurately. They become familiar with the protractor’s scale and how to align it correctly with the angle’s vertex and arms.
Angle Identification – Students practice identifying different types of angles, such as acute, obtuse, right, and straight angles. This skill helps them recognize the characteristics of each angle type and understand their properties.
Angle Measurement – Measuring angles to the nearest degree is a fundamental skill emphasized in these worksheets. Students learn to read the protractor scale accurately and record their measurements precisely.
Spatial Awareness – By measuring angles in various orientations, students develop their spatial awareness and ability to visualize geometric concepts. This skill is crucial for understanding more advanced geometry and practical applications.
Types of Problems
Identifying and Measuring Individual Angles – One common type of problem on measuring angles geometry worksheets involves identifying and measuring individual angles. These exercises typically present students with a variety of geometric figures, such as triangles, quadrilaterals, or other polygons, and ask them to measure specific angles using a protractor. Students must accurately place the protractor, align it correctly, and read the measurement. This type of problem helps students become proficient in using geometric tools and understanding the basic properties of angles. Additionally, these exercises reinforce the importance of precision and accuracy in mathematical measurements. By consistently practicing these skills, students build a solid foundation in basic geometry.
Finding Missing Angles in Polygons – Another type of problem commonly found on these worksheets involves finding missing angles in polygons. Students are given a polygon with some angle measures provided and are required to calculate the missing angles based on the properties of the polygon. For example, in a triangle, students use the fact that the sum of the interior angles is always 180 degrees to find the unknown angle. In a quadrilateral, they use the sum of 360 degrees. These problems help students understand the relationships between angles in various shapes and reinforce their ability to apply geometric rules and formulas. By working through these exercises, students enhance their problem-solving skills and deepen their understanding of polygon properties.
Angle Bisectors and Perpendicular Bisectors – Worksheets might include problems that require students to draw and identify angle bisectors and perpendicular bisectors. These exercises involve using a compass and straightedge to accurately bisect given angles or line segments, reinforcing students’ skills in geometric constructions. For instance, students might be asked to bisect a 60-degree angle and then measure the resulting 30-degree angles to verify their work. These types of problems not only teach geometric construction techniques but also help students understand the concept of dividing angles and segments into equal parts. This practice is crucial for developing spatial reasoning and precision in geometric constructions.
Complementary and Supplementary Angles – Problems involving complementary and supplementary angles are also common on measuring angles worksheets. These exercises present pairs of angles and ask students to identify whether they are complementary (summing to 90 degrees) or supplementary (summing to 180 degrees). Students may also be required to calculate the measure of one angle given the measure of its complement or supplement. For example, if one angle is 35 degrees, students must determine that its complement is 55 degrees and its supplement is 145 degrees. These problems help students understand and apply the relationships between angles, enhancing their ability to work with angle pairs in various geometric contexts.
Vertical and Adjacent Angles – Worksheets often include problems focused on vertical and adjacent angles. Vertical angles are the pairs of opposite angles formed when two lines intersect, and they are always equal. Adjacent angles share a common vertex and a common side but do not overlap. Students might be given diagrams of intersecting lines and asked to identify and measure vertical and adjacent angles. For instance, if one angle is 50 degrees, students must identify the vertical angle as also 50 degrees and calculate the adjacent angles based on their supplementary relationship. These exercises reinforce students’ understanding of angle relationships and help them practice identifying and measuring angles in various geometric configurations.
Angles Formed by Parallel Lines and a Transversal – A more advanced type of problem involves angles formed by parallel lines and a transversal. Students are presented with diagrams of two parallel lines intersected by a transversal, creating various angle pairs such as corresponding, alternate interior, alternate exterior, and consecutive interior angles. Problems might ask students to identify these angles and use their properties to calculate unknown angle measures. For example, if one corresponding angle is 120 degrees, students must determine that all other corresponding and alternate interior angles are also 120 degrees, while consecutive interior angles sum to 180 degrees. These exercises help students understand the properties of angles in parallel line configurations and apply this knowledge to solve complex problems.
Angle Estimation Exercises – Some worksheets might include angle estimation exercises, where students are asked to estimate the measure of given angles without using a protractor. These problems develop students’ ability to visually assess and approximate angle measures, which is a valuable skill in both academic and real-life contexts. Students practice making educated guesses about angle sizes, which helps them develop a better intuitive understanding of angles and their relationships. This skill is particularly useful in situations where precise measurement tools are not available, and quick, approximate judgments are needed.
Real World Applications
Measuring angles is a fundamental skill that finds numerous applications in the real world, making it an essential part of mathematical education. Angles are everywhere, from the design of buildings and furniture to the navigation of vehicles and the creation of art. By learning how to measure angles, students gain the ability to understand and interact with the world around them more effectively.
In architecture and construction, measuring angles is crucial for designing buildings and other structures. Architects and engineers use angles to ensure that walls meet correctly, roofs are pitched properly, and various components of a building fit together as planned. For instance, the precise measurement of angles ensures that a roof can adequately support snow load or that a staircase meets safety regulations. Construction workers also rely on angle measurements to cut materials accurately and to assemble components with the necessary precision.
Students might come across the need to measure angles in various everyday activities. For example, when they help in cooking, they may need to cut ingredients at specific angles to follow a recipe or to create a particular presentation. In sports, understanding angles can improve performance; for instance, a basketball player needs to consider the angle of their shot to make a basket, or a pool player must calculate angles to make successful shots. Additionally, angles play a significant role in navigation, whether using a map and compass or understanding the angles at which to turn when driving.
The skills related to measuring angles are foundational for various fields, including science, technology, engineering, and mathematics (STEM). In science, students may use angle measurements in experiments involving light reflection and refraction or in studying the angles of celestial bodies. In technology, creating computer graphics and animations involves precise angle calculations to render images correctly. Engineering disciplines, from civil to mechanical, require accurate angle measurements to design and analyze systems and structures.
The ability to measure and understand angles enhances critical thinking and problem-solving skills. When students measure angles, they learn to be precise and methodical, which are essential skills in any scientific or technical endeavor. This practice also helps them develop spatial awareness, allowing them to visualize and manipulate objects in their minds, a skill useful in fields like robotics, video game design, and even surgery.