Corresponding Angles Worksheets
About These 15 Worksheets
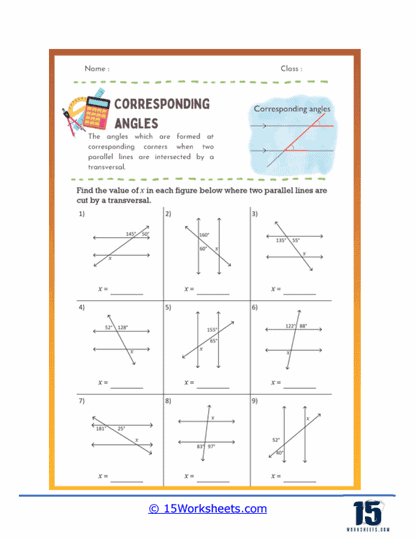
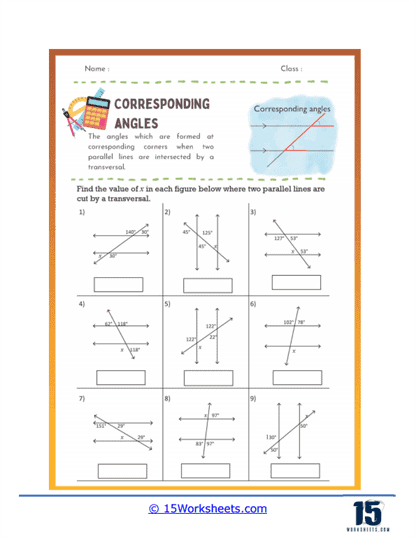
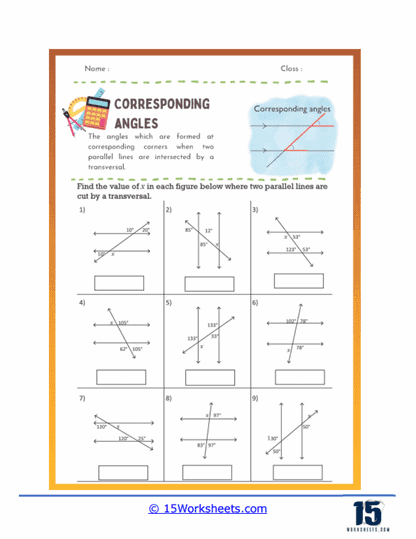
These worksheets will help students understand and practice the concept of corresponding angles, which are angles that occupy the same relative position at each intersection where a transversal crosses two parallel lines. These worksheets typically feature a variety of diagrams where parallel lines are intersected by one or more transversals, presenting students with opportunities to identify, measure, and calculate corresponding angles. The primary objective of these worksheets is to enhance students’ geometric reasoning and their ability to recognize angle relationships in different geometric configurations.
What Are Corresponding Angles?
Corresponding angles are pairs of angles that occur when a transversal intersects two parallel lines. They are located on the same side of the transversal and in corresponding positions relative to the parallel lines. Specifically, one angle is exterior (outside the parallel lines) while the other is interior (between the parallel lines), but both are on the same side of the transversal. These angles are always congruent, meaning they have equal measures. Understanding corresponding angles helps in solving geometric problems involving parallel lines and transversals. They are fundamental in proving theorems and properties related to parallel lines. Recognizing and working with corresponding angles is essential in fields like architecture, engineering, and design, where precise angle measurements are crucial.
Types of Exercises
Corresponding angles worksheets offer a range of exercises designed to solidify students’ understanding of this geometric concept. Here are some common types of exercises found in these worksheets:
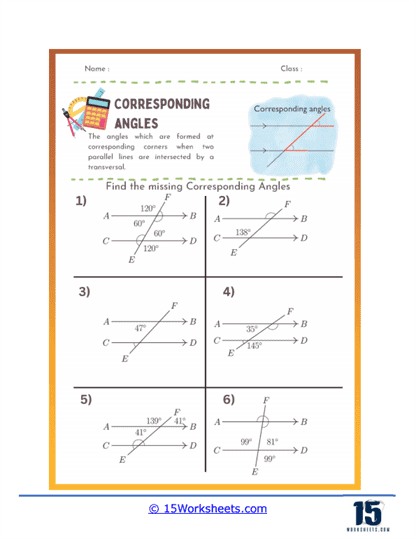
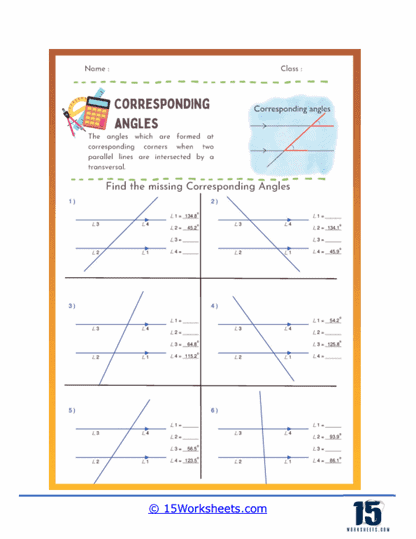
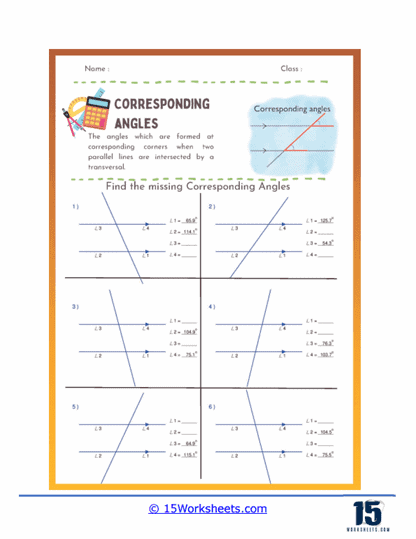
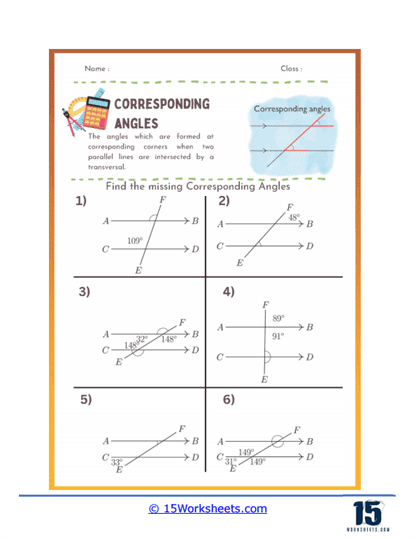
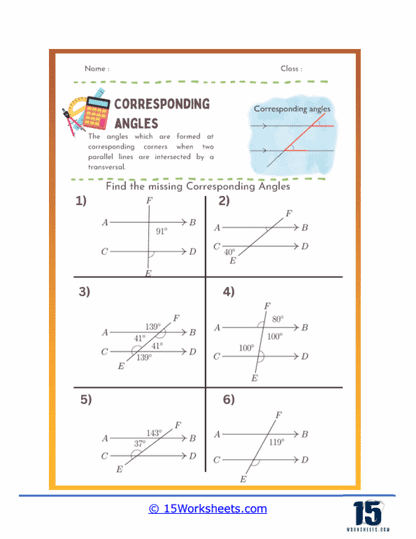
Identification of Corresponding Angles – These exercises present diagrams with parallel lines and a transversal. Students are asked to identify pairs of corresponding angles. This helps them practice visual recognition of corresponding angles and understand their positions.
Measuring Angles – Some worksheets include diagrams with given angles, and students must measure the corresponding angles using a protractor. This exercise reinforces the practical application of angle measurement tools and the properties of corresponding angles.
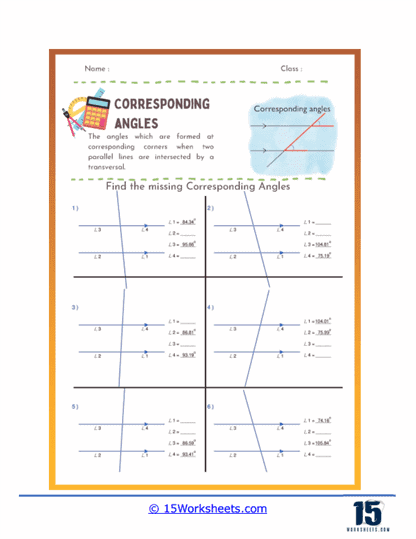
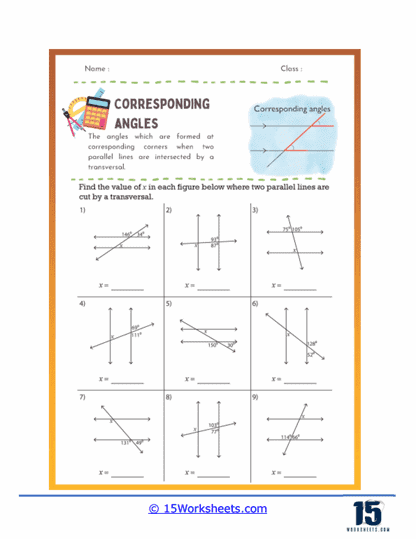
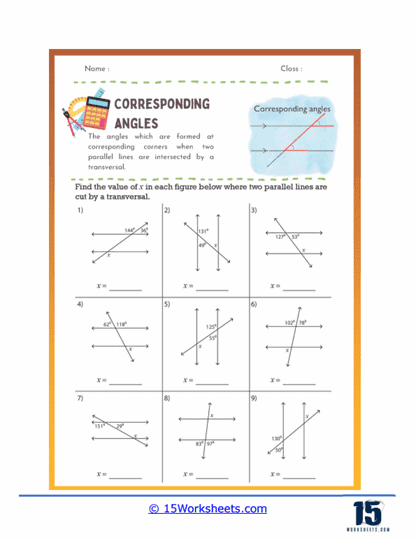
Finding Missing Angles – These problems provide some angle measures and require students to calculate the missing corresponding angles. For instance, if ∠1 is 60 degrees, students need to find ∠2 which corresponds to ∠1.
Multiple Transversals – Advanced worksheets might feature diagrams where multiple transversals intersect parallel lines. Students must identify and calculate corresponding angles created by these intersections, adding complexity to their practice.
Real-World Applications – Some worksheets incorporate real-world scenarios where students apply their knowledge of corresponding angles. For example, they might analyze architectural designs or street layouts to find corresponding angles, making the learning process more engaging and relevant.
Proof-Based Problems – Higher-level worksheets might include proof-based problems where students must use logical reasoning to prove that certain angles are corresponding angles and therefore equal. This develops their ability to construct and understand geometric proofs.
Benefits of These Worksheets
Enhancing Geometric Understanding
Corresponding angles worksheets play a crucial role in enhancing students’ understanding of geometry. By consistently working with diagrams of parallel lines and transversals, students become familiar with the visual and theoretical aspects of corresponding angles. This foundational knowledge is essential for more advanced geometric concepts and problem-solving. As students practice identifying and working with corresponding angles, they build a strong conceptual framework that supports their learning in other areas of mathematics. This repeated exposure to key geometric principles helps solidify their understanding, making it easier to grasp more complex topics later on. Furthermore, a deep understanding of corresponding angles is vital for mastering theorems and proofs related to parallel lines and transversals.
Developing Critical Thinking Skills
These worksheets encourage critical thinking as students must apply the properties of corresponding angles to solve problems. Whether identifying, measuring, or calculating angles, students engage in analytical thinking, which is valuable across all areas of mathematics and beyond. The ability to think critically and logically is a key skill developed through these exercises. By encountering various problems that require them to analyze relationships between angles and make deductions based on geometric principles, students enhance their problem-solving abilities. This skill not only benefits their mathematical studies but also equips them with the ability to approach challenges methodically in other academic subjects and real-life situations.
Promoting Precision and Accuracy
Working with corresponding angles requires students to be precise and accurate, especially in measurement and calculation tasks. Using protractors to measure angles and ensuring that calculations are correct fosters attention to detail, an important skill in both academic and real-world contexts. These worksheets help students develop a meticulous approach to problem-solving. As they practice measuring and verifying angle relationships, students learn the importance of accuracy in mathematics. This focus on precision is essential for success in fields such as engineering, architecture, and any profession that relies on exact measurements and careful planning.
Building a Strong Mathematical Foundation
A solid understanding of corresponding angles is foundational for success in higher-level geometry and other areas of mathematics. Mastery of this concept prepares students for more complex topics such as triangle congruence, similarity, and the properties of polygons. Corresponding angles worksheets ensure that students build this strong mathematical foundation early on. By mastering these fundamental concepts, students are better equipped to tackle more advanced mathematical problems and theories. This preparation is crucial for academic progression, providing a seamless transition from basic geometric principles to more sophisticated mathematical challenges.
Varied Problem Types
The diverse range of problems found in corresponding angles worksheets ensures comprehensive practice. From simple identification tasks to complex proof-based problems, these worksheets cater to different learning levels and styles. This variety keeps students motivated and challenged, promoting continuous learning and improvement. By encountering a wide array of problem types, students can develop a robust understanding of corresponding angles and their applications. This comprehensive practice helps students build confidence in their abilities, ensuring they are well-prepared for both academic assessments and real-world applications of geometry.
Real-World Applications of Corresponding Angles
Corresponding angles are not just theoretical constructs confined to the classroom; they have practical applications that permeate various aspects of the real world. Understanding corresponding angles and their properties equips students with skills that are applicable in numerous fields, from architecture to navigation. In architecture, for instance, precise angle measurements are crucial for designing buildings and ensuring structural integrity. Engineers use corresponding angles to design machinery and components that fit together seamlessly. In navigation, pilots and sailors use angle calculations to determine their courses and ensure they reach their destinations accurately. These applications highlight the importance of mastering corresponding angles for various professional paths.
Teachers can enhance students’ learning by incorporating real-world scenarios into their lessons on corresponding angles. For example, students might be asked to design a simple structure using craft materials, applying their knowledge of angles to ensure stability and symmetry. Alternatively, they might analyze maps and plan routes, using angles to determine the most efficient paths. These activities help students see the relevance of corresponding angles, making their learning experience more engaging and meaningful. By connecting mathematical concepts to real-life situations, educators can inspire students to appreciate the practical value of their studies, fostering a deeper interest in geometry and its applications.
By incorporating real-world scenarios, corresponding angles worksheets make learning more engaging and relevant. Students see the practical applications of geometric concepts in fields such as architecture, engineering, and design. This not only enhances their interest in the subject but also demonstrates the importance of geometry in everyday life. Understanding how corresponding angles are used in real-world contexts helps students appreciate the value of their mathematical education. For example, recognizing that architects use these angles to design buildings or that engineers rely on them for constructing bridges makes the subject matter more tangible and significant.
Everyday Problem-Solving
Even in everyday life, understanding corresponding angles can be beneficial. When hanging pictures or shelves at home, knowing how to measure and match angles ensures that items are level and aligned. DIY enthusiasts and hobbyists frequently use these principles when creating projects that require precise measurements and fitting parts together. Students who grasp corresponding angles can apply this knowledge to solve practical problems around the house, making their daily tasks easier and more efficient. Whether assembling furniture or ensuring that home improvements are done correctly, the skills learned from corresponding angles worksheets are incredibly useful in day-to-day activities.