Classifying Angles Worksheets
About These 15 Worksheets
These worksheets will help students understand, identify, and differentiate between various types of angles. These worksheets are essential components of the mathematics curriculum, particularly in geometry, as they provide practical exercises for students to apply theoretical knowledge. The primary objective of these worksheets is to enhance students’ ability to recognize different angles in various contexts, ranging from simple geometric figures to complex real-world applications.
These worksheets typically present a variety of angles that students must identify and categorize as acute, obtuse, right, reflex, or straight. They are visually engaging and often include a mix of diagrams, real-life images, and abstract shapes to ensure a comprehensive understanding of the topic. The exercises on these worksheets are designed to be progressively challenging, starting with basic identification tasks and moving towards more complex classification and application problems.
What Are The Common Angle Classifications?
Acute Angles
Acute angles are those that measure less than 90 degrees. These angles are sharp and can be found in various geometric shapes, such as triangles, where at least two angles are often acute. Understanding acute angles is fundamental in geometry, as they frequently appear in different configurations and play a crucial role in the properties of polygons. For example, in an acute triangle, all three interior angles are less than 90 degrees, making the triangle a specific type of geometric figure with unique properties. Recognizing and measuring acute angles helps students develop a keen sense of angle relationships and spatial reasoning.
Right Angles
Right angles measure exactly 90 degrees and are one of the most recognizable and important types of angles in geometry. They are often marked with a small square at the vertex to denote their exact measure. Right angles are fundamental in many aspects of geometry and everyday life, as they are used to define perpendicular lines and form the basis of various geometric shapes such as squares and rectangles. In practical applications, right angles are crucial in construction, engineering, and design, ensuring that structures and components meet at precise and stable junctions. The ability to identify and work with right angles is essential for students, as it forms the foundation for more complex geometric and algebraic concepts.
Obtuse Angles
Obtuse angles measure more than 90 degrees but less than 180 degrees. These angles appear wider and are commonly found in various geometric configurations, such as obtuse triangles, which contain one obtuse angle and two acute angles. Understanding obtuse angles helps students recognize the diversity of angle types and their implications in different shapes and figures. For instance, in polygons, the presence of obtuse angles affects the overall shape and internal angle sum of the figure. In real-world contexts, obtuse angles are used in design and architecture to create specific aesthetic effects and functional structures that require angles greater than 90 degrees.
Straight Angles
Straight angles measure exactly 180 degrees and are essentially a straight line. These angles are important in understanding the concept of supplementary angles, where two angles add up to form a straight angle. In geometric proofs and constructions, straight angles are used to establish relationships between angles and lines, providing a basis for understanding parallel lines and transversals. In practical applications, straight angles are crucial in fields such as surveying and navigation, where accurate linear measurements are essential. Recognizing straight angles helps students comprehend how angles interact to form linear paths and structures.
Reflex Angles
Reflex angles measure more than 180 degrees but less than 360 degrees. These angles represent a larger sweep and are often used to describe angles that go beyond a straight line. Reflex angles are important in advanced geometric studies and applications, such as in rotational symmetry and certain design elements that require a broader range of motion. In real-world scenarios, reflex angles can be observed in mechanical systems and various design fields, where components need to rotate or pivot through large angles. Understanding reflex angles helps students appreciate the full spectrum of angle measurements and their applications in complex geometric and practical situations.
Full Angles
Full angles measure exactly 360 degrees and represent a complete rotation around a point. These angles are fundamental in understanding circular motion and rotational symmetry. Full angles are used in various fields, including trigonometry, physics, and engineering, where rotational dynamics are essential. In geometry, full angles help students understand the concept of angle sum and the relationship between rotation and angle measures. Recognizing full angles is crucial for comprehending cyclic patterns and motions, as well as for solving problems involving circular paths and rotational systems.
Adjacent Angles
Adjacent angles share a common vertex and a common side but do not overlap. These angles are positioned next to each other and are often found in geometric figures such as polygons and complex shapes. Understanding adjacent angles is important for solving problems related to angle measurement and construction, as they frequently appear in practical applications. In real-world contexts, adjacent angles are used in tasks such as tiling, carpentry, and any activities requiring precise angle measurements to ensure parts fit together seamlessly. Recognizing and calculating adjacent angles helps students develop spatial awareness and accuracy in geometric constructions.
Complementary Angles
Complementary angles are pairs of angles whose measures add up to 90 degrees. These angles are often found in right triangles and other geometric configurations that require precise angle measures. Understanding complementary angles is essential for constructing geometric shapes and solving problems involving right angles. In practical applications, complementary angles are used in various design and engineering tasks to ensure that components meet at precise angles. Recognizing complementary angles helps students develop a strong foundation in geometry and enhances their ability to solve problems involving angle relationships.
Supplementary Angles
Supplementary angles are pairs of angles whose measures total 180 degrees. These angles are typically found on a straight line, where two adjacent angles combine to form a straight angle. Understanding supplementary angles is crucial in geometry as they help explain the properties of straight lines and the relationships between intersecting lines. In real-world applications, supplementary angles are used in designing and analyzing structures that rely on linear and angular measurements to ensure that components fit together seamlessly and maintain structural integrity. Recognizing supplementary angles helps students develop a deeper understanding of geometric principles and their practical applications.
Vertical Angles
Vertical angles are pairs of opposite angles formed when two lines intersect. These angles are always congruent, meaning they have equal measures. Vertical angles are fundamental in geometric proofs and constructions because they provide a reliable way to identify equal angles in various configurations. In everyday life, vertical angles can be observed in many situations where lines intersect, such as in the crossing of roads, the design of window panes, and various other structural elements where symmetry and balance are important. Understanding vertical angles helps students develop critical thinking skills and enhances their ability to solve geometric problems.
Types of Exercises
Classifying Angles worksheets feature a wide range of exercises and practice problems designed to reinforce learning and ensure mastery of the topic. Below are some common types of exercises found in these worksheets:
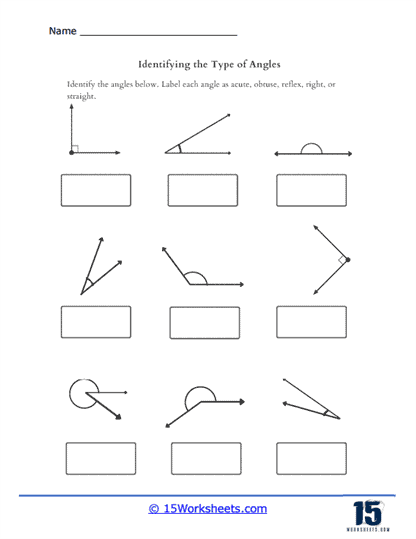
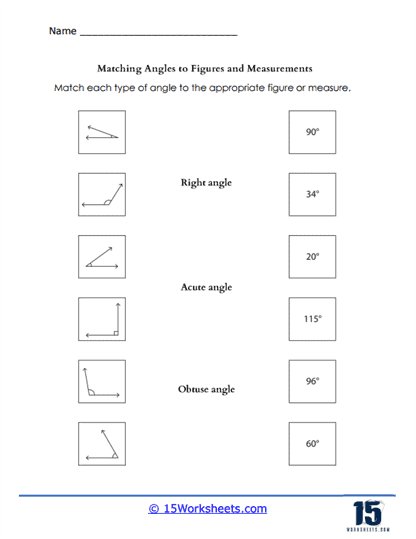
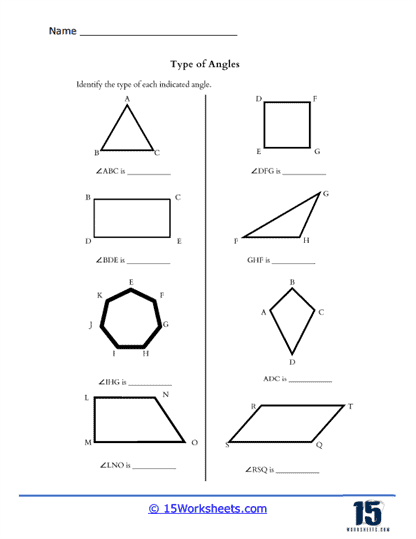
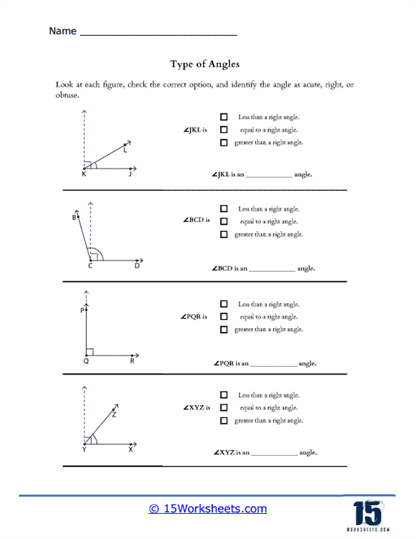
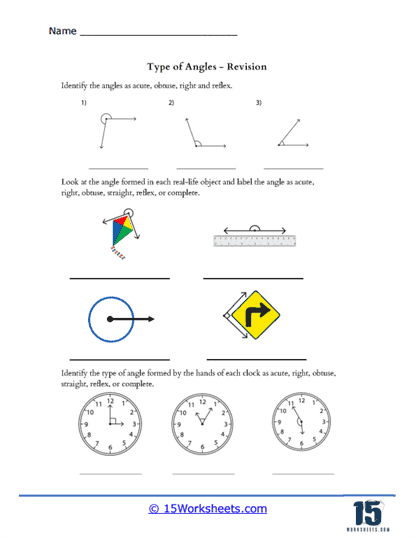
Basic Identification – Students are presented with a variety of angles and must identify each one as acute, obtuse, right, reflex, or straight. This exercise typically involves simple geometric shapes and serves as an introduction to angle classification. Students learn to identify different types of angles based on their measurements. Acute angles measure less than 90 degrees, obtuse angles measure more than 90 degrees but less than 180 degrees, right angles measure exactly 90 degrees, reflex angles measure more than 180 degrees but less than 360 degrees, and straight angles measure exactly 180 degrees.
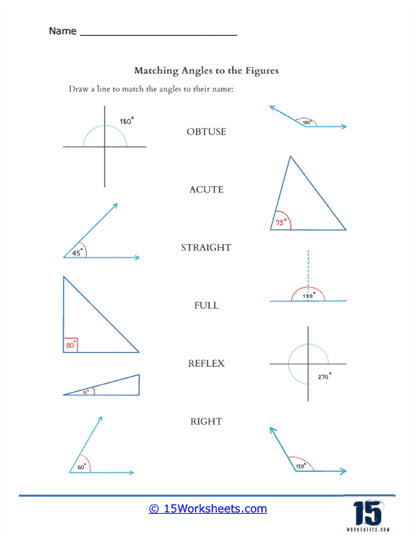
Matching Angles to Names – Students draw lines connecting angles to their correct names. This exercise helps reinforce the terminology associated with different angles. By working with different shapes and angles, students develop better spatial awareness. They learn to visualize and mentally manipulate shapes, which is a key skill in geometry.
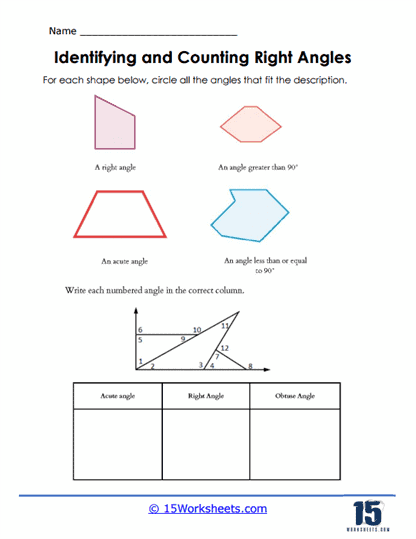
Labeling Angles in Figures – Worksheets present students with complex shapes and require them to label the angles within these shapes. This exercise helps students understand how angles are part of larger geometric figures.
Classifying Angles in Real-Life Images – These worksheet includes real-life images where students must identify and classify angles. This type of exercise helps students apply their knowledge to everyday situations, making learning more relevant and engaging.
Drawing and Measuring Angles – Some worksheets may require students to draw angles of specific measurements using a protractor. This exercise not only reinforces the concept of angle measurement but also improves students’ skills in using mathematical tools. Classifying angles requires students to analyze and compare different angles, fostering critical thinking and analytical skills.
Angle Addition and Subtraction – Advanced worksheets may include problems where students must find the measure of unknown angles by adding or subtracting known angles. This type of problem enhances their problem-solving skills and understanding of angle relationships.
Benefits of These Worksheets
Improved Analytical Skills
By identifying and comparing angles, students develop strong analytical and critical thinking skills. Classifying Angles worksheets require students to analyze the properties of each angle, measure them accurately, and determine their classifications based on specific criteria. This process enhances their ability to think logically and methodically, skills that are valuable not only in mathematics but also in other subjects and real-life situations. For instance, the critical thinking skills honed through these exercises can be applied to scientific research, engineering problems, and even everyday decision-making processes. The rigorous practice of analyzing angles fosters a mindset geared towards precision, reasoning, and problem-solving.
Practical Application
Including real-life images and scenarios in these worksheets helps students see the practical applications of their mathematical knowledge. By relating angle classification to everyday objects and situations, such as the angles in a piece of furniture, the slope of a roof, or the structure of a bridge, students can better appreciate the relevance of what they are learning. This practical application makes learning more engaging and motivates students to see the value of geometry in the world around them. Additionally, understanding how to classify angles in real-life contexts prepares students for careers in fields such as architecture, engineering, and design, where precise angle measurement and classification are crucial.
Visual Learning
The visual nature of these worksheets caters to visual learners, helping them understand abstract concepts through diagrams and images. Visual aids, such as colorful diagrams, clear illustrations, and real-life photographs, enhance comprehension and retention by making abstract geometric concepts more tangible. This approach is particularly effective for students who struggle with traditional text-based learning methods. By seeing angles in various contexts, students can better grasp the concept and apply their knowledge more effectively. The use of visual learning tools also supports diverse learning styles, ensuring that all students have the opportunity to succeed in understanding geometry.
Versatility in Teaching
Teachers can use these worksheets in various ways, including individual practice, group activities, homework assignments, and assessments. This versatility makes them a valuable resource in the classroom, allowing educators to adapt their teaching strategies to meet the needs of their students. For instance, worksheets can be used as a quick assessment tool to gauge students’ understanding, as a collaborative group activity to encourage peer learning, or as homework to reinforce classroom instruction. This flexibility ensures that students receive comprehensive instruction in angle classification, tailored to their individual learning paces and preferences. Furthermore, the ability to use these worksheets in different settings promotes a well-rounded educational experience.
Progressive Difficulty
The progressive nature of the exercises ensures that students can build their skills gradually. Starting with basic identification tasks, such as recognizing and labeling angles, and moving to more complex problems, like solving for unknown angles in geometric figures, helps ensure a thorough understanding of the topic. This gradual increase in difficulty allows students to build confidence as they master each level before moving on to more challenging tasks. By scaffolding the learning process, these worksheets support continuous improvement and mastery of geometric concepts. This methodical approach to skill-building prepares students for more advanced studies and helps prevent gaps in their understanding.
Engagement and Motivation
The interactive and visually engaging nature of these worksheets keeps students motivated and interested in learning. Creative titles like “Angle Zoo Safari!” and “Angle Explorer’s Treasure Hunt!” add an element of excitement and adventure to the learning process, transforming routine exercises into fun and engaging activities. This gamified approach to education not only captures students’ attention but also encourages active participation and sustained interest in geometry. By making learning enjoyable, these worksheets help students develop a positive attitude towards mathematics, fostering a lifelong interest in the subject. This engagement is critical for maintaining motivation and ensuring that students remain invested in their educational journey.
Real World Applications
Classifying angles is a fundamental skill in geometry that has numerous practical applications in the real world. Students learn to classify angles to better understand and engage with various real-life contexts and problems. This knowledge is not only crucial for academic success but also for everyday situations that involve spatial awareness and problem-solving.
One of the most direct applications of classifying angles is in construction and architecture. Architects and engineers routinely use angles to design buildings, bridges, and other structures. Accurate measurement and classification of angles ensure that structures are safe, functional, and aesthetically pleasing. For instance, ensuring that a corner is a perfect right angle is crucial in constructing stable and level buildings. When students classify angles, they gain insight into how different structures maintain their integrity and functionality.
In the classroom, students might come across angles in subjects like physics, where understanding angles is crucial for studying forces and motion. For example, the angle of incidence in optics determines how light behaves when it strikes a surface. Similarly, understanding angles is important in mechanics, where the direction and magnitude of forces are analyzed. By classifying angles, students can better grasp these physical concepts and their applications.
Understanding angles enhances problem-solving and critical-thinking skills. When students classify angles, they learn to observe, analyze, and draw conclusions based on geometric properties. These skills are transferable to various aspects of life, from making informed decisions to solving complex problems. The ability to classify and work with angles fosters a logical and systematic approach to thinking, which is valuable in both academic and real-world contexts.