Angle Postulate Worksheets
About These 15 Worksheets
These worksheets will help students understand and apply geometric principles related to angles. These worksheets typically include a variety of exercises and problems aimed at reinforcing the fundamental concepts of angles within geometric contexts. They serve as tools for educators to assess and enhance students’ comprehension and proficiency in geometry, specifically focusing on the properties and relationships of angles.
What Is The Angle Postulate?
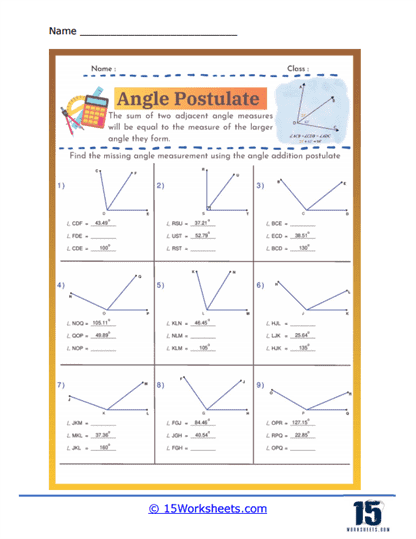
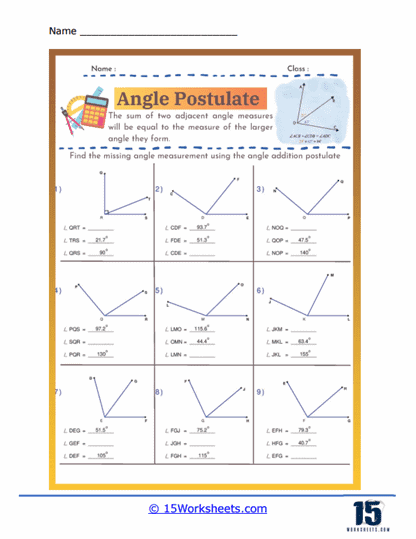
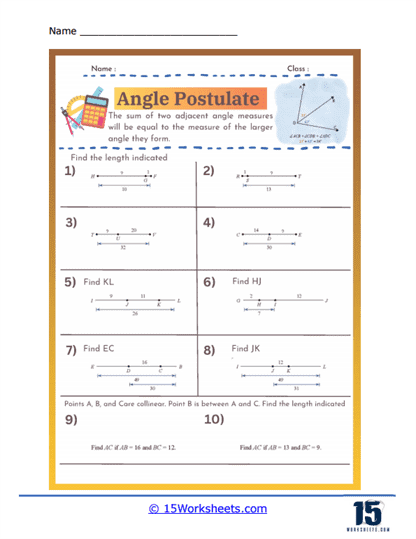
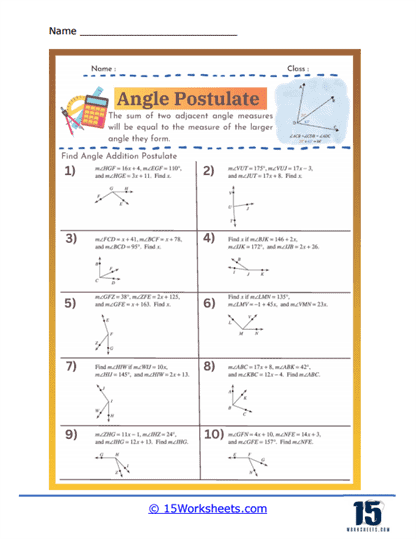
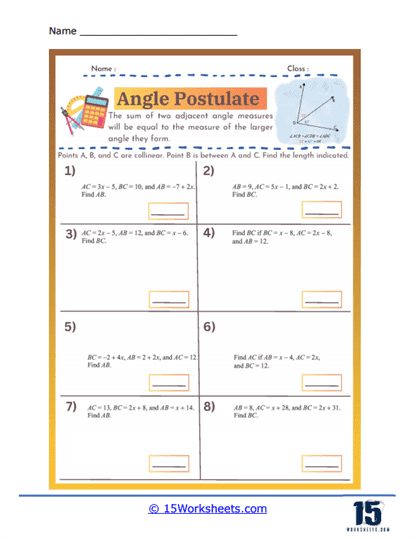
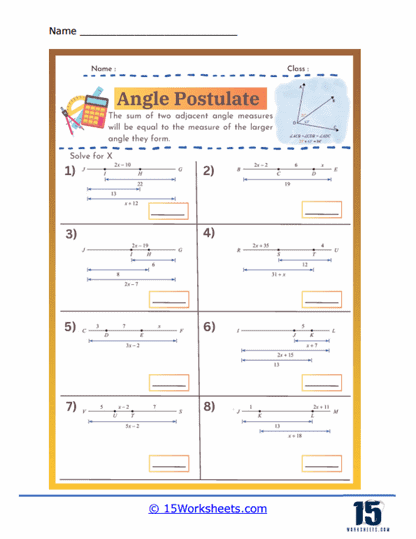
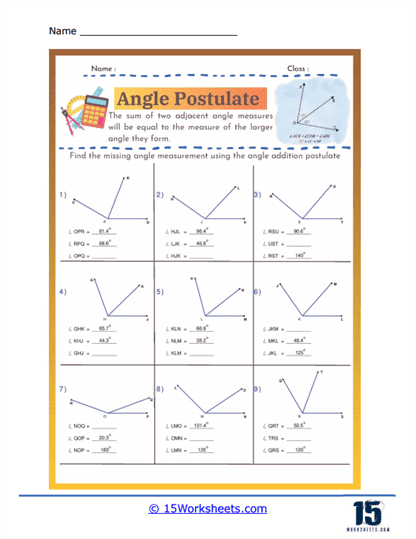
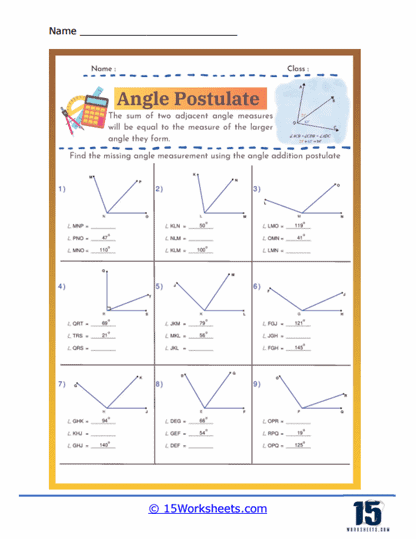
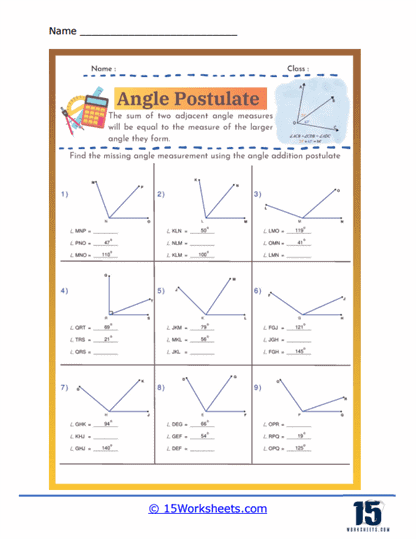
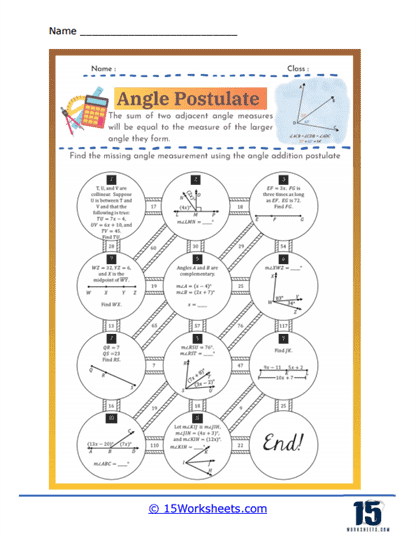
The Angle Addition Postulate states that if a point lies inside an angle, the angle formed by the two smaller angles created is equal to the original angle. Specifically, if point B lies in the interior of ∠AOC, then ∠AOB + ∠BOC = ∠AOC. This postulate is fundamental in geometry as it allows for the measurement and calculation of angles within complex figures. It is essential for proving the properties of geometric shapes and solving problems involving angle measurements. Understanding the Angle Addition Postulate aids in comprehending how angles interact and combine in geometric constructions. This principle is widely used in various applications, from basic geometric proofs to advanced fields such as architecture and engineering. Mastery of the Angle Addition Postulate enhances logical reasoning and analytical skills in geometry.
Math Skills Explored
These worksheets delve into several essential math skills. Students learn to identify and classify different types of angles, such as acute, obtuse, right, and straight angles. This classification helps them understand the basic characteristics of angles based on their measurements. Students explore angle measurement, learning how to use protractors or other measuring tools to determine the size of angles in degrees. This skill is crucial for accurately describing and comparing angles in geometric figures. Students practice angle relationships, such as complementary and supplementary angles, which deepen their understanding of how angles interact within shapes and diagrams.
Types of Exercises
These worksheets feature a variety of exercises to reinforce learning. These include identifying angles in geometric figures, where students must locate and label angles based on given descriptions or diagrams. Another common exercise involves measuring angles using protractors, where students apply their knowledge of angle measurement to determine the precise degrees of various angles. Additionally, worksheets often include problems on angle relationships, requiring students to solve for unknown angles or identify specific angle pairs (e.g., vertical angles, corresponding angles) within geometric configurations. Problem-solving tasks may also involve applying the properties of angles to solve real-world scenarios or geometric puzzles, promoting critical thinking and practical application of geometric concepts.
Benefits of Angle Postulate Worksheets
Using angle postulate worksheets offers numerous benefits to both students and educators, significantly enhancing the learning process in geometry. These worksheets provide a structured and systematic approach to practicing and understanding geometric principles, particularly those related to angle postulates. By working through these worksheets, students can reinforce classroom learning and consolidate their understanding independently, ensuring that they grasp fundamental concepts thoroughly.
Reinforcement of Classroom Learning
Angle postulate worksheets reinforce classroom instruction by providing additional practice that helps students internalize geometric principles. This reinforcement is crucial as it allows students to revisit and apply what they have learned in various contexts, solidifying their comprehension and retention of key concepts. The structured nature of these worksheets ensures that students systematically cover all necessary aspects of angle postulates, building a strong foundational knowledge in geometry.
Active Engagement with Geometry
These worksheets encourage active engagement with geometry through hands-on activities such as measuring angles and solving angle-related problems. Active learning is more effective than passive methods, as it involves students directly in the learning process, making abstract concepts more tangible and understandable. By actively participating in these exercises, students develop a deeper comprehension of geometric concepts, which enhances their ability to apply these principles in different scenarios.
Development of Critical Thinking Skills
Angle postulate worksheets challenge students to think critically and solve problems, fostering the development of important analytical and reasoning skills. By encountering various problems that require them to apply angle postulates, students learn to approach geometric problems methodically and develop strategies for finding solutions. This critical thinking is essential not only in geometry but also in other areas of mathematics and real-world problem-solving.
Targeted Support and Differentiation
For educators, angle postulate worksheets are invaluable tools for assessing students’ progress and identifying areas where additional instruction or practice is needed. This capability allows teachers to provide targeted support and differentiate their teaching methods to meet the diverse needs of their students. By pinpointing specific areas of difficulty, educators can tailor their instruction to address individual learning gaps, ensuring that all students achieve a solid understanding of geometric principles.
Preparation for Advanced Studies
Mastering the concepts covered in angle postulate worksheets prepares students for more advanced mathematical studies. A solid understanding of angle postulates is foundational for higher-level topics such as trigonometry, calculus, and various branches of engineering and physics. These worksheets ensure that students have the necessary skills and knowledge to succeed in these advanced subjects, providing a seamless transition from basic geometry to more complex mathematical concepts.
Real-World Examples
Understanding angles is essential in many real-world applications, particularly in fields such as architecture and engineering. For instance, architects must consider angles when designing structures to ensure both stability and aesthetics. They use geometric principles to calculate angles for supporting structures like beams and columns, as well as for designing angles in building facades and interiors. Precise angle measurements are crucial for creating visually appealing and structurally sound buildings.
Engineers also rely heavily on angle measurements to design components for machines and devices. Ensuring that parts fit together correctly and function smoothly often depends on accurately understanding and applying angle postulates. For example, in mechanical engineering, the alignment of gears and other moving parts requires precise angle calculations to ensure efficient operation and avoid mechanical failures.
The ability to accurately measure and understand angles extends beyond the classroom and is crucial in practical applications. Mastering angle postulates through dedicated worksheets helps students see the relevance of geometric concepts in everyday life and various professions, demonstrating the importance of geometric literacy.