Inscribed Angles Worksheets
About These 15 Worksheets
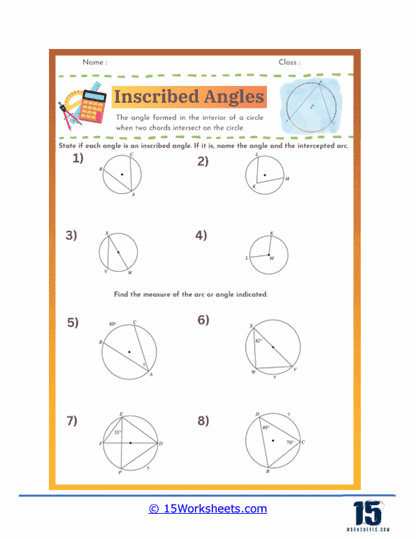
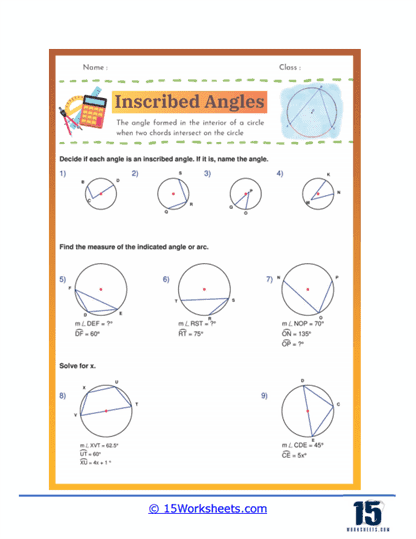
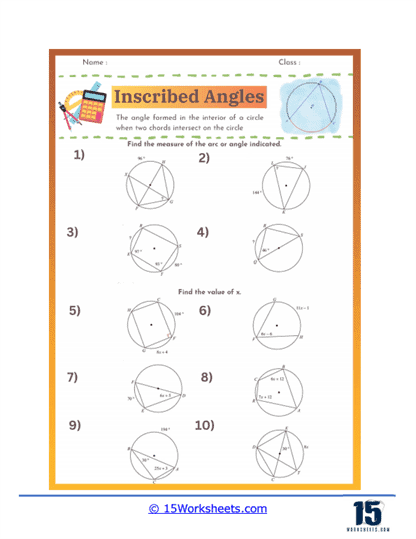
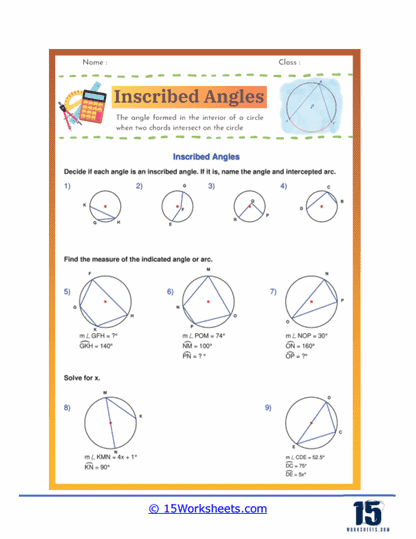
These worksheets will help students understand and practice the concept of inscribed angles in circles. An inscribed angle is formed by two chords in a circle that share an endpoint on the circle. The vertex of the inscribed angle lies on the circle, and the angle itself intercepts an arc between the endpoints of the chords. These worksheets aim to provide students with a solid understanding of this geometric concept through a variety of exercises and practice problems. By working through these worksheets, students learn to identify inscribed angles, apply related geometric theorems, and solve problems involving circles and angles.
What Are Inscribed Angles?
Inscribed angles are angles formed by two chords in a circle that meet at a common endpoint on the circle’s circumference. The vertex of an inscribed angle lies on the circle itself, and its sides, or arms, extend to intersect the circle at two other points. A key property of inscribed angles is that they subtend, or “cut off,” an arc of the circle. This means that the measure of the inscribed angle is half the measure of the arc it intercepts. Inscribed angles that intercept the same arc or congruent arcs are always equal. This property is useful in solving various geometric problems and proving theorems related to circles. Inscribed angles are fundamental in the study of circles and play a significant role in understanding cyclic quadrilaterals, where all vertices lie on the circumference of a circle. Recognizing and working with inscribed angles helps in grasping more complex geometric relationships and properties within circles.
Math Skills Explored
Inscribed angle worksheets cover a range of important math skills that are fundamental to geometry. Firstly, students learn to identify inscribed angles and distinguish them from other types of angles in circles, such as central angles. This skill is crucial for accurately applying geometric principles and solving related problems. The worksheets reinforce the understanding that the measure of an inscribed angle is always half the measure of the intercepted arc. This principle is a key geometric theorem that students must master to solve problems involving circles.
In addition to identifying and measuring inscribed angles, students practice calculating the measures of intercepted arcs and other related angles. These calculations often involve applying the properties of inscribed angles, central angles, and the relationships between different angles in a circle. By combining these principles, students can solve for unknown measures in complex diagrams. These exercises help develop algebraic skills, as students frequently set up and solve equations to find the measures of unknown angles and arcs.
Another important skill explored in these worksheets is the ability to use geometric notation correctly. Students learn to label angles, arcs, chords, and points accurately, which is essential for clear communication in geometry. This notation practice supports their ability to follow and create geometric proofs, an advanced skill that is crucial for higher-level math courses.
Types of Exercises
Inscribed angle worksheets feature a variety of exercises and practice problems designed to reinforce the concepts and skills mentioned above. These problems range from basic identification tasks to more complex calculations and proof-based questions. Here are some common types of exercises found on inscribed angle worksheets:
Identification of Inscribed Angles – One of the foundational exercises in these worksheets involves identifying inscribed angles in various diagrams. Students are presented with circles containing multiple angles and chords and are asked to mark or color the inscribed angles. This exercise helps them visually recognize the geometric relationships and understand the concept of inscribed angles being half the measure of their intercepted arcs. Often, these identification problems serve as the first step before moving on to calculation-based questions.
Calculating the Measure of Inscribed Angles – A significant portion of inscribed angle worksheets focuses on calculating the measures of inscribed angles. These problems typically provide the measure of an intercepted arc or a central angle, and students must use the property that an inscribed angle is half the measure of its intercepted arc to find the angle measure. These exercises often require setting up and solving algebraic equations, reinforcing both geometric and algebraic skills.
Finding Intercepted Arc Measures – Some worksheets include problems where students are given the measure of an inscribed angle and must find the measure of the intercepted arc. This exercise requires students to apply the inscribed angle theorem in reverse, multiplying the angle measure by two to find the arc measure. These problems help students understand the direct relationship between inscribed angles and their intercepted arcs and develop their ability to manipulate geometric relationships.
Word Problems – Some worksheets incorporate word problems that require the application of inscribed angle principles to real-world scenarios. For instance, a problem might describe a situation involving a Ferris wheel, and students must calculate angles or arc measures based on given information. These word problems help students see the practical applications of inscribed angles and enhance their problem-solving abilities by requiring them to translate verbal descriptions into geometric diagrams and equations.
Angle Relationships in Circles – Some worksheets extend the concept of inscribed angles to explore relationships between different angles and arcs in circles. For example, students might work with problems involving central angles, inscribed angles, and angles formed by intersecting chords or tangents. These exercises require students to apply multiple geometric principles and understand the interplay between different types of angles and arcs in a circle. Solving these problems helps students develop a comprehensive understanding of angle relationships in circles.
Proofs Involving Inscribed Angles – Advanced inscribed angle worksheets might include proof-based problems where students must use logical reasoning to demonstrate geometric theorems involving inscribed angles. These exercises develop critical thinking and understanding of geometric properties. Proofs might involve multiple steps and the use of other geometric principles, such as the relationships between inscribed angles and opposite arcs, or the properties of cyclic quadrilaterals. Writing out these proofs helps students articulate their reasoning and understand the logical flow of geometric arguments.
Mixed Review Problems – To reinforce learning and ensure mastery, many inscribed angle worksheets include mixed review problems that combine different types of exercises. These worksheets might present a series of diagrams where students need to identify inscribed angles, calculate unknown measures, find intercepted arc measures, and prove angle relationships in one comprehensive activity. Mixed review problems help students apply their knowledge in varied contexts and build confidence in their geometric skills.
Benefits of These Worksheets
Enhanced Understanding of Circle Geometry
Inscribed angle worksheets play a crucial role in enhancing students’ understanding of circle geometry. By working through these worksheets, students become familiar with the properties and relationships specific to inscribed angles and their intercepted arcs. This foundational knowledge is essential for grasping more advanced concepts related to circles, such as the relationships between central angles, chords, and tangents. Through consistent practice, students develop a comprehensive understanding of how inscribed angles function within the broader context of circle geometry, preparing them for more complex mathematical studies.
Development of Analytical Skills
Inscribed angle worksheets require students to apply logical reasoning and critical thinking to solve problems. As they work through various exercises, students must identify inscribed angles, calculate their measures, and understand their relationships with intercepted arcs and other angles. This analytical approach helps students develop strong problem-solving skills, which are valuable not only in mathematics but also in other academic disciplines and real-life situations. By learning to approach problems methodically and think critically, students enhance their overall cognitive abilities and become more adept at tackling challenging tasks.
Reinforcement of Key Geometric Concepts
These worksheets reinforce key geometric concepts by providing numerous opportunities for students to apply their knowledge of inscribed angles in different contexts. For example, students might be asked to prove that inscribed angles intercepting the same arc are congruent or to use inscribed angles to solve for unknown measures in geometric figures. This repetition and variation help solidify students’ understanding and improve their ability to recall and apply geometric principles. Reinforcing these concepts through practice ensures that students retain the information and can use it effectively in future mathematical endeavors.
Practical Application of Mathematical Skills
Inscribed angle worksheets provide practical applications of mathematical skills, particularly in the context of geometry. Students practice measuring angles, calculating arc lengths, and understanding the relationships between different geometric elements within a circle. These skills are not only essential for academic success but also have practical applications in fields such as engineering, architecture, and design. By working through real-world problems involving inscribed angles, students see the relevance of geometry in everyday life and gain a deeper appreciation for the subject.
Visual Learning and Comprehension
The visual nature of inscribed angle worksheets caters to visual learners and helps students understand abstract concepts through diagrams and illustrations. Visual aids, such as circle diagrams with marked inscribed angles and arcs, make it easier for students to grasp the relationships between different geometric elements. This visual approach enhances comprehension and retention by making abstract geometric principles more concrete and accessible. By seeing the concepts in action, students can better understand how inscribed angles function and how to apply their properties in various situations.
Versatility in Teaching
Inscribed angle worksheets are versatile tools that teachers can use in various instructional settings, including individual practice, group activities, homework assignments, and assessments. This versatility makes them valuable resources in the classroom, allowing educators to tailor their teaching strategies to meet the needs of their students. For instance, worksheets can be used to introduce new concepts, reinforce previously learned material, or assess students’ understanding of inscribed angles. This flexibility ensures that students receive comprehensive instruction and multiple opportunities to practice and master the concepts.
Progressive Difficulty for Skill Building
The progressive nature of inscribed angle worksheets ensures that students can build their skills gradually. Starting with basic identification and measurement tasks and progressing to more complex problems involving proofs and applications helps ensure a thorough understanding of the topic. This gradual increase in difficulty allows students to build confidence as they master each level before moving on to more challenging tasks. By scaffolding the learning process, these worksheets support continuous improvement and mastery of geometric concepts, preparing students for more advanced studies.
Engagement and Motivation
Inscribed angle worksheets often include engaging and interactive elements that keep students motivated and interested in learning. Activities such as puzzle-solving, real-world problem scenarios, and creative design tasks make learning about inscribed angles enjoyable and relevant. By incorporating elements of fun and challenge, these worksheets encourage active participation and sustained interest in geometry. This engagement is critical for maintaining students’ motivation and fostering a positive attitude towards mathematics, which can lead to greater academic success and a lifelong interest in the subject.