Alternate Angles Worksheets
About These 15 Worksheets
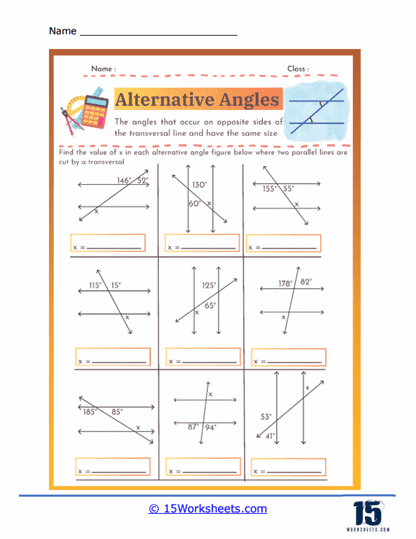
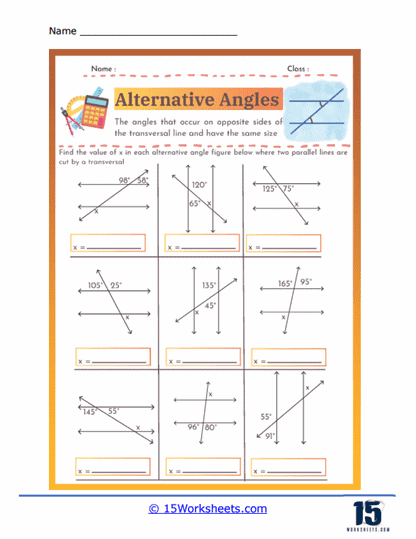
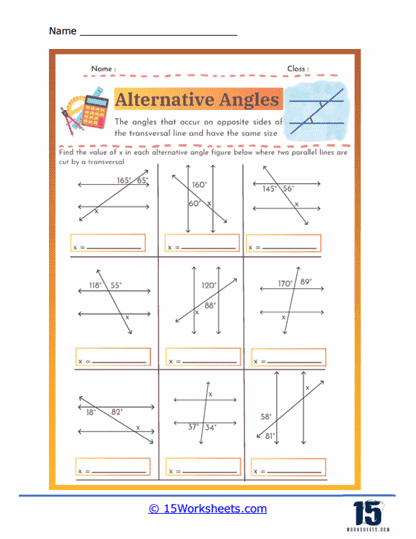
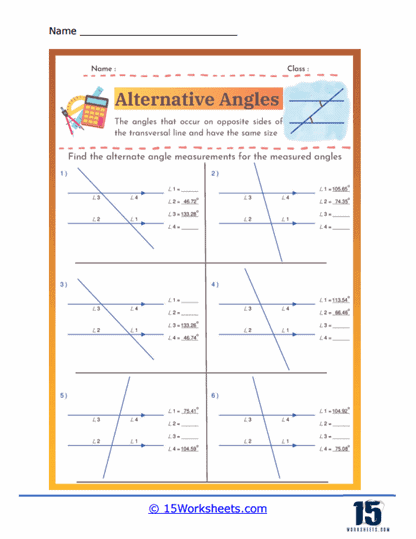
These worksheets are will help students understand and practice the concept of alternate angles. These angles are formed when a transversal line crosses two parallel lines, creating pairs of angles that are equal in measure. Specifically, alternate interior angles are located between the two parallel lines on opposite sides of the transversal, while alternate exterior angles are found outside the parallel lines, also on opposite sides of the transversal. These worksheets typically include a variety of exercises that require students to identify alternate angles, calculate their measures, and apply their understanding to solve geometric problems.
What Are Alternate Angles?
Alternate angles are pairs of angles that occur on opposite sides of a transversal when it intersects two parallel lines. There are two types: alternate interior angles, which lie between the parallel lines, and alternate exterior angles, which lie outside the parallel lines. Both types of alternate angles are congruent, meaning they have equal measures. This property is fundamental in proving various geometric theorems and solving problems involving parallel lines and transversals. Understanding alternate angles helps in identifying relationships between angles and developing logical reasoning in geometry. They are essential in fields such as architecture, engineering, and design, where precise angle measurements are crucial. Recognizing and using alternate angles simplifies the analysis of complex geometric figures and real-world structures.
Math Skills Explored
Alternate angles worksheets focus on several important math skills, including:
Angle Identification – Students learn to identify alternate interior and exterior angles in various geometric configurations. This skill requires careful observation and a solid understanding of the definitions of these angles.
Angle Measurement – Worksheets often include exercises where students must calculate the measures of unknown angles. This involves using the property that alternate angles are congruent, meaning they have the same measure.
Problem-Solving – Students apply their knowledge of alternate angles to solve more complex problems. This might involve finding missing angle measures in polygons, working with parallel lines cut by transversals, or proving geometric theorems.
Critical Thinking – Understanding alternate angles and their properties requires logical reasoning and the ability to apply geometric principles to new situations. This skill is developed through practice and problem-solving.
Benefits of Alternate Angles Worksheets
Using alternate angles worksheets in the classroom offers a range of benefits that go beyond simple practice, contributing to a comprehensive understanding of geometric concepts and enhancing students’ overall mathematical skills. Here are the expanded advantages of incorporating these worksheets into the learning process:
Enhanced Understanding
Alternate angles worksheets provide structured and repetitive practice that aids students in internalizing the concept of alternate angles and their properties. By repeatedly working through problems that involve alternate angles, students develop a deeper comprehension of how these angles function within geometric figures. This foundational understanding is crucial not only for success in geometry but also for advanced mathematics and related fields. When students grasp the properties and applications of alternate angles, they are better equipped to tackle more complex geometric problems with confidence and accuracy.
Skill Development
Through regular practice with alternate angles worksheets, students develop essential mathematical skills. These include angle identification, precise measurement, problem-solving, and logical reasoning. Mastery of these skills is not only beneficial in academic settings but also in various career paths that require analytical thinking and precision. For instance, fields such as engineering, architecture, and computer science often require a solid understanding of geometric principles. By honing these skills through worksheets, students prepare themselves for future professional challenges and opportunities.
Engagement and Motivation
Well-designed alternate angles worksheets can significantly enhance student engagement and motivation in learning geometry. By incorporating a variety of exercises, puzzles, and real-world applications, these worksheets make learning more interactive and enjoyable. When students see the relevance of geometric concepts in everyday life, they are more likely to be motivated to learn and apply their knowledge. Engaging worksheets that challenge students and provide a sense of accomplishment can foster a positive attitude towards mathematics and encourage continuous learning.
Assessment and Feedback
Teachers can effectively use alternate angles worksheets as a tool for assessing students’ understanding and providing targeted feedback. By analyzing students’ performance on these worksheets, teachers can identify areas where students may struggle and need additional support. This allows for personalized instruction that addresses individual learning needs. Providing timely and specific feedback helps students improve their understanding and correct any misconceptions, leading to a more robust grasp of geometric concepts.
Real-World Example
Consider a situation where an architect is designing a bridge with parallel supports and needs to determine the angles formed by the supporting beams. Understanding alternate angles is crucial in this context to ensure the bridge’s structural integrity and aesthetic appeal. Suppose the angle formed by one beam and the ground is 45°. Knowing that this angle and the corresponding angle on the opposite side of the support are alternate interior angles, the architect can confidently state that the angle on the opposite side is also 45°. This application of alternate angles ensures that the beams are properly aligned, contributing to the stability and symmetry of the bridge design. By leveraging their knowledge of alternate angles, the architect can create a bridge that is not only functional but also visually harmonious.