Powers of Products Worksheets
About These 15 Worksheets
These worksheets were meticulously created to enhance a student’s grasp of exponent rules, particularly focusing on the application of exponents to products. These worksheets serve as a pivotal tool in the mathematical curriculum, aiming to solidify the foundational concept that when a product of two or more factors is raised to a power, the exponent applies to each factor within the product. This principle is crucial for simplifying complex algebraic expressions and solving problems efficiently in higher-level math, science, and engineering courses.
The core principle behind Powers of Products Worksheets is the rule that (ab)n = anbn, where a and b represent any numbers or variables, and n is the exponent. This rule indicates that when a product is raised to a power, the exponent applies to each term in the product separately. It’s a fundamental property of exponents that allows for the simplification and manipulation of expressions involving powers of products, fostering a deeper understanding of algebraic structures and the properties of exponents.
By engaging with a variety of exercises, students not only learn the rule itself but also develop a deeper understanding of algebraic expressions and enhance their problem-solving skills. These worksheets prepare students for more advanced mathematical challenges, fostering a solid foundation in algebra that will support their academic and professional pursuits in fields where mathematics is essential. Through diligent practice, students can achieve proficiency in this fundamental aspect of algebra, opening the door to a wide range of mathematical and scientific endeavors.
Types of Exercises
Our powers of products worksheets include a diverse array of exercises tailored to practice and reinforce different aspects of applying exponents to products. These exercises range from introductory to more advanced levels, catering to the varied learning stages of students. Here’s an overview of the types of exercises typically found on these worksheets:
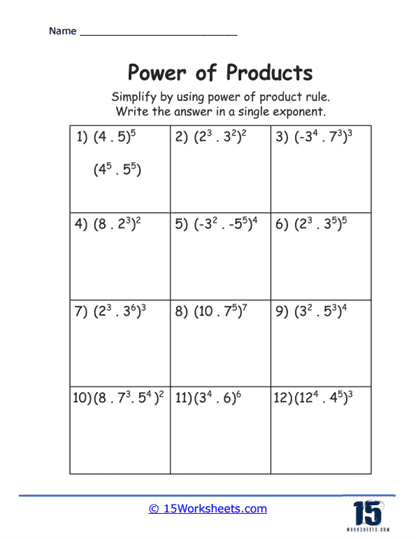
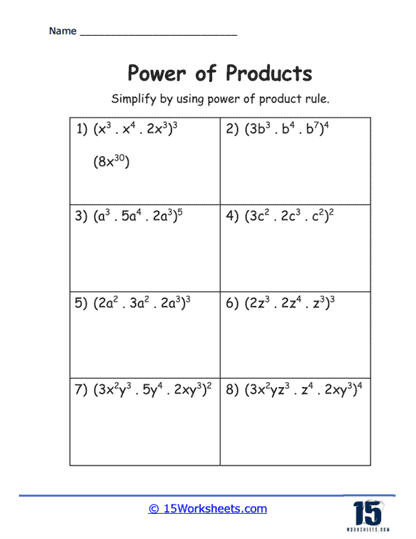
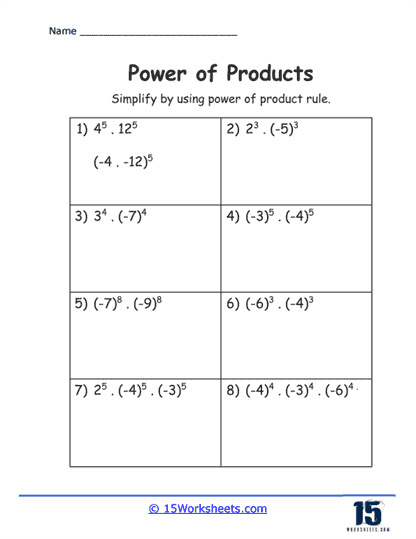
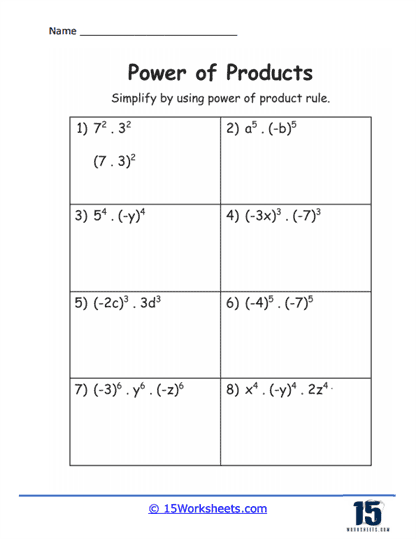
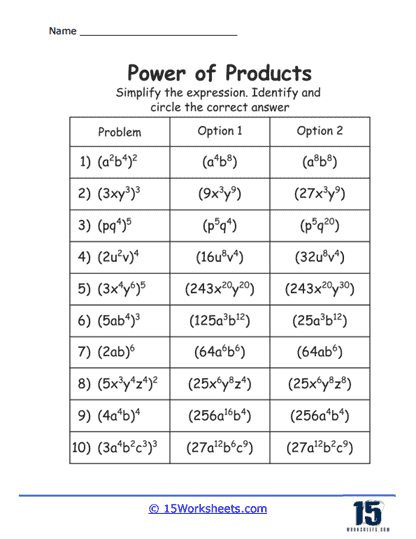
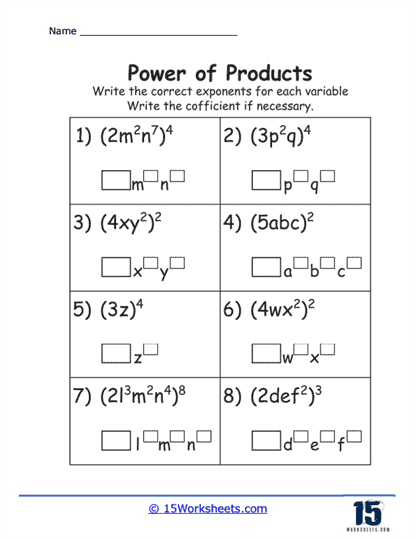
Basic Multiplication to Powers – The simplest exercises involve applying a power to a basic multiplication problem, such as (2 x 3)2. These problems help students understand the initial concept of applying the exponent to each factor separately.
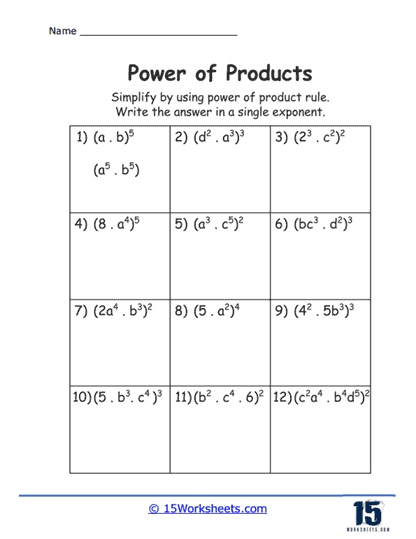
Variable Expressions – As students progress, exercises start incorporating variables, such as (xy)3. These problems require students to apply the exponent to each variable in the product, aiding in the understanding of how the rule extends to algebraic expressions.
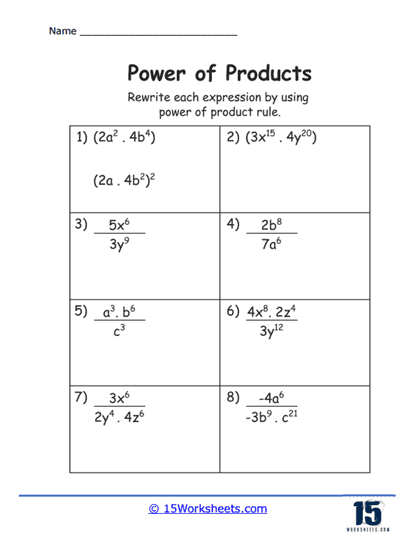
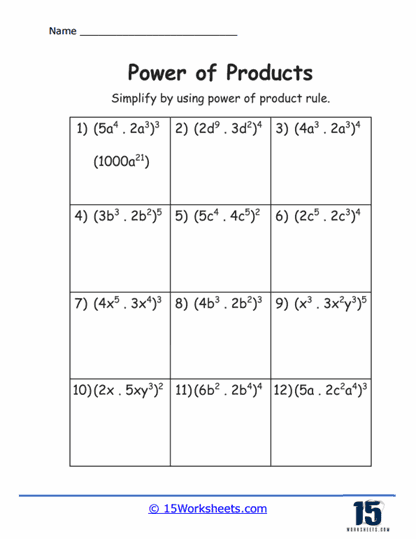
Multiple Factors – More complex exercises involve products with more than two factors, such as (2xy)4. Students practice applying the exponent to each factor within the product, enhancing their ability to handle larger and more complex expressions.
Mixed Numeric and Algebraic Factors – Exercises that combine both numbers and variables within the product, like
(3x2y)3, challenge students to apply exponents to both types of factors. These problems improve students’ skills in manipulating mixed expressions.
Application in Formulas – Some worksheets may include exercises where students apply the power of a product rule to simplify expressions found in geometric or scientific formulas. For example, simplifying the volume formula of a cube when the side length is given as a product raised to a power.
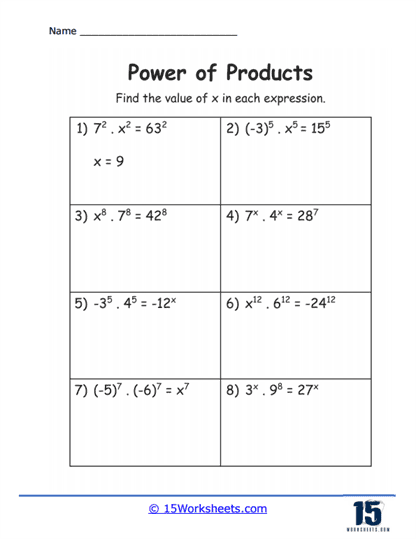
Comparative Problems – Exercises that require students to compare expressions or determine the simplified form of one expression versus another test the student’s understanding and application skills. These problems often involve critical thinking and a deeper comprehension of exponent rules.
The Benefits Of These Worksheets
Reinforcement of Exponent Rules – Continuous practice with these worksheets helps in reinforcing the understanding of how exponent rules work, particularly the power of a product rule. This reinforcement is crucial for students to become fluent in manipulating expressions with exponents.
Building Algebraic Proficiency – Through the manipulation of algebraic expressions involving products raised to powers, students enhance their algebraic skills. This proficiency is fundamental for success in higher mathematics, where algebra serves as a cornerstone.
Improving Problem-Solving Skills – The variety of exercises on these worksheets challenges students to apply the power of a product rule in different contexts, thereby improving their problem-solving abilities. The ability to break down and simplify complex problems is a valuable skill in mathematics and beyond.
Preparation for Advanced Topics – Mastery of the powers of products rule prepares students for more advanced topics in mathematics, physics, and engineering, where the manipulation of expressions and formulas becomes increasingly complex.
Confidence Building – As students become more comfortable and proficient in using the power of a product rule, their confidence in handling exponents and algebraic expressions grows. This confidence can lead to better performance in mathematics overall.
What is the Power of a Product Property of Exponents?
This is a fundamental rule in mathematics that simplifies the process of working with exponents, especially when dealing with products raised to a power. This property is instrumental in both simplifying algebraic expressions and solving complex mathematical problems, serving as a cornerstone in the study of algebra and calculus. Understanding and applying this rule can significantly enhance a student’s ability to manipulate and understand mathematical expressions involving exponents.
The Power of a Product Property states that when a product of two or more factors is raised to an exponent, the exponent applies to each factor within the product individually. The formal expression of this rule is:
(ab)n = anbn
, where a and b are any real numbers, variables, or expressions, and n is the exponent.
This rule can extend to products of more than two factors as well, such as:
(abc)n = anbncn
The essence of this rule lies in its ability to distribute the exponent across each factor in the product separately. This distribution is based on the properties of exponents, which dictate how to handle multiplication and division of powers. The Power of a Product Property simplifies expressions by allowing each component of the product to be dealt with individually, making it easier to perform further algebraic manipulations or calculations.
How Is The Power of a Product Property Used In the Real World?
The Power of a Product Property of Exponents is not just a mathematical principle confined to textbooks; it’s a vital tool that finds application in various real-world scenarios, enhancing our ability to solve complex problems across multiple disciplines. This foundational concept in mathematics simplifies calculations involving products raised to powers, making it indispensable in fields ranging from physics and engineering to finance, computer science, and beyond.
In Physics and Engineering
In the realms of physics and engineering, this mathematical property streamlines the analysis of physical phenomena and the design of systems. Whether calculating the energy stored in electrical components, determining forces and work, or analyzing the dynamics of structures, engineers and physicists rely on this principle to break down complex equations. It allows for a clearer understanding and manipulation of variables and constants, facilitating precise calculations and innovations in technology and infrastructure.
Financial Applications
The finance sector greatly benefits from this principle, especially in the computation of compound interest, a cornerstone of savings strategies, loan structures, and investment planning. Simplifying the process of forecasting future values of financial instruments, it enables individuals and institutions to make informed decisions. By applying this principle, financial analysts and economists can model economic phenomena, predict market trends, and develop strategies that influence fiscal policy and investment decisions.
Computer Science and Algorithm Design
In computer science, the optimization of algorithms—procedures or formulas for solving problems—often involves this property. It’s crucial in expressing the computational complexity of algorithms, helping programmers and developers enhance the efficiency and performance of software and systems. Understanding how to manipulate expressions involving powers of products is key to developing solutions that scale with growing data sizes and complexities.
Chemistry and Pharmacology
The field of chemistry utilizes this property to calculate reaction rates and concentrations, essential for understanding how substances interact under various conditions. Similarly, pharmacology applies this principle in determining medication dosages based on factors like body weight, ensuring efficacy and safety in treatments. These applications demonstrate how the principle aids in the precise formulation and analysis of chemical and biological processes.
Acoustics and Sound Engineering
In acoustics, the design and optimization of audio equipment and environments benefit from the ability to simplify calculations related to sound intensity and distribution. This principle assists sound engineers in creating systems that deliver clear and balanced audio, whether in consumer electronics, concert halls, or public spaces, showcasing the intersection of mathematics, physics, and technology.
Economic Modeling
Economists employ this principle to model complex interactions within markets and predict future economic conditions. By simplifying expressions that describe economic trends, inflation rates, and other indicators, this property helps in crafting models that can inform policy decisions and strategic planning. It underscores the role of mathematics in understanding and navigating the economic landscape.
The Broad Impact of the Principle
The Power of a Product Property of Exponents underscores the profound relationship between abstract mathematical principles and practical problem-solving across diverse fields. By enabling the simplification of complex expressions and calculations, it enhances our ability to understand the world, design and optimize systems and technologies, and make informed decisions in finance and economics. This principle exemplifies how foundational mathematical concepts are indispensable tools in our quest to analyze, innovate, and evolve in an increasingly complex world. Through its applications, we see the tangible benefits of mathematics in improving processes, technologies, and understanding across a broad spectrum of disciplines.