Exponents Worksheets
About These 15 Worksheets
These worksheets will help students practice and master the concept of exponents, which are a fundamental component of mathematics. Exponents represent repeated multiplication of a base number, and understanding them is crucial for navigating more advanced mathematical topics such as algebra, geometry, and calculus. These worksheets typically include a variety of exercises that challenge students to compute the value of numbers raised to certain powers, apply the laws of exponents in simplifying expressions, and solve equations involving exponents. By presenting problems in a structured and incremental manner, exponent math worksheets cater to learners at different skill levels, facilitating a step-by-step comprehension of exponents and their properties.
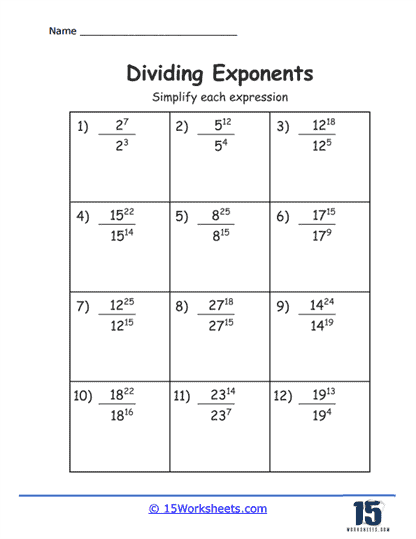
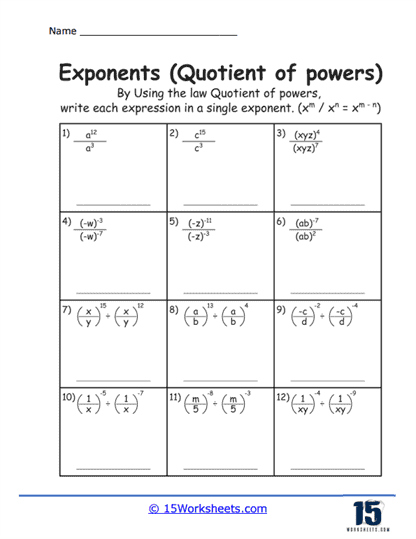
Students practice and master the division of numbers with exponents, focusing on applying specific rules like the quotient of powers rule. These worksheets guide learners through exercises that challenge them to simplify expressions and solve problems by dividing powers with the same base, enhancing their understanding and proficiency in managing exponent-based calculations.
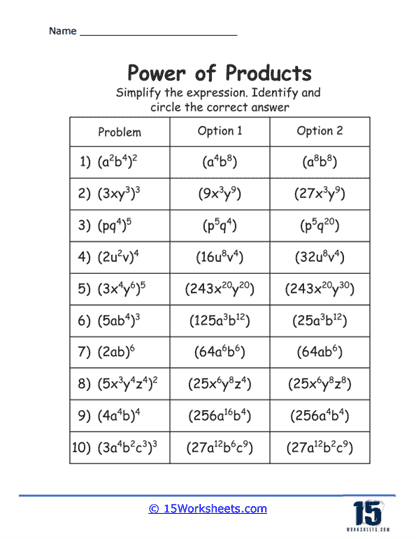
These worksheets help students practice and understand the multiplication of numbers with exponents, particularly focusing on the use of the product of powers rule. These worksheets provide exercises that require learners to multiply powers with the same base and thus add the exponents, facilitating their ability to simplify expressions and solve related mathematical problems efficiently.
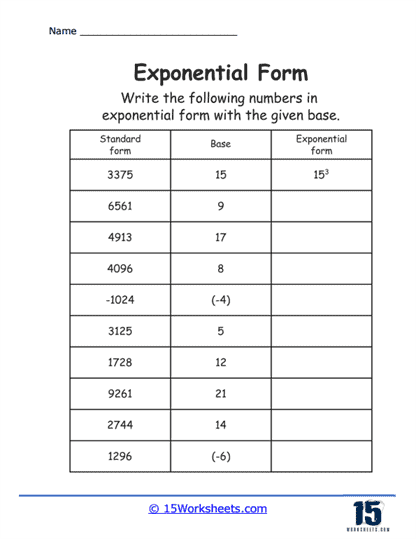
The focus on these sheets is how to express numbers using exponents, converting between standard numerical forms and exponential notation. These worksheets guide learners through exercises that involve writing large numbers or fractions in a more compact, exponent-based format, enhancing their understanding of and proficiency with exponential expressions.
Exponents with Fractional Bases
These worksheets delve into the realm of raising fractions to powers, offering students a path to explore how fractional bases interact with exponents. These resources challenge learners with exercises that apply exponential rules to fractions, broadening their mathematical understanding and skill in handling complex expressions.
These worksheets introduce students to the foundational rules governing the operations on exponential expressions, such as multiplication and division of powers, raising a power to a power, and zero and negative exponents. Through engaging exercises, these worksheets equip learners with the skills to manipulate and simplify expressions using these laws, enhancing their mathematical fluency and problem-solving capabilities.
These worksheets provide prompts that focus students to unearth the hidden base or exponent that makes an equation true. Through this investigative process, learners sharpen their algebraic reasoning and become adept at navigating the interplay between exponents and their bases, enhancing their problem-solving toolkit.
These worksheets focus on the complexities of executing basic arithmetic operations-addition, subtraction, multiplication, and division-when exponents enter the fray. These sheets guide learners through the maze of combining exponential expressions, ensuring they grasp the intricacies of manipulating powers in varied mathematical contexts.
They provide a structured pathway for learners to practice and master the nuance of raising fractions or division operations to a power, fostering a deeper comprehension of exponent rules and their applications.
Engaging learners with hands-on practice, these worksheets distill the essence of distributing exponents over factors, empowering students with the prowess to simplify complex expressions with confidence.
Reciprocals and Inverses of Exponents
These worksheets engage students in exercises that demystify how to handle reciprocal bases and the inversion of exponent values, fostering an enriched understanding of symmetry and balance in the realm of exponents.
Through a sequence of straightforward exercises, these worksheets initiate students into the world of exponents, laying the groundwork for more complex mathematical explorations by instilling an initial fluency with simple power expressions.
What is an Exponent in Math?
An exponent in mathematics is a number that indicates how many times a base number is to be multiplied by itself. The exponent is usually written as a small number to the upper right of the base number. For example, in the expression 23, 2 is the base, and 3 is the exponent, meaning that 2 is to be multiplied by itself 3 times (2 x 2 x 2 = 8). Exponents are a fundamental part of algebra and are used to express large numbers more compactly, perform multiplications and divisions of numbers with the same base more efficiently, and solve various mathematical problems involving exponential growth or decay.
Beyond the realm of pure mathematics, exponents are used in a wide range of real-life situations and fields. One common application is in compound interest calculations in finance, where exponents help determine the amount of interest accrued on an investment over time. In science, exponents are integral to the laws of physics, chemistry, and biology, such as when calculating the intensity of earthquakes using the Richter scale, describing the exponential growth of bacteria populations, or understanding the decay of radioactive substances. Exponents also play a crucial role in computer science, particularly in algorithms related to data processing and in representing very large or very small numbers in scientific notation, as seen in computer programming and digital storage capacity (e.g., bytes in powers of 2). Additionally, in engineering, exponents are used to model phenomena like sound intensity levels (decibels), and in electronics, they help in calculating electrical power using Ohm’s law. Through these examples, it’s clear that exponents are not only a critical mathematical tool but also a versatile concept applied across various disciplines to solve practical problems.
The use of exponent math worksheets significantly enhances student math skills by promoting consistent practice, reinforcing memory retention, and encouraging analytical thinking. As students work through these worksheets, they become more familiar with exponent rules, such as the product of powers, quotient of powers, and power of a power, which are pivotal in simplifying and solving more complex mathematical problems.
This repetitive practice not only improves their ability to handle exponents with confidence but also lays a solid foundation for tackling higher-level math challenges. Moreover, these worksheets often include problem-solving and critical thinking questions that compel students to apply their knowledge in various contexts, thereby enhancing their problem-solving skills and mathematical fluency.
How Do We Use Exponents in Everyday Life?
Exponents, often recognized for their mathematical significance, extend their utility far beyond the confines of algebraic expressions, permeating various facets of everyday life. They are essentially a shorthand for expressing the multiplication of a number by itself multiple times, simplifying complex calculations and concepts into more manageable forms. Here’s a detailed exploration of three common real-life scenarios where exponents play a crucial role, highlighting their practicality and omnipresence.
Compound Interest in Financial Growth
One of the realms where exponents find significant application is in the world of finance, specifically in the calculation of compound interest. This concept is pivotal in understanding how investments grow over time. Compound interest differs from simple interest by not just accumulating on the initial principal amount but also on the interest that has been previously earned. This means that the amount of interest earned grows at an exponential rate as it is continually recalculated on an increasingly larger base. Consequently, savings accounts, loans, and investments can grow (or in the case of loans, cost) significantly more due to the effect of compounding, showcasing the exponential potential of financial decisions.
Exponential Growth and Decay in Nature and Science
The principles of exponential growth and decay find extensive application in various scientific disciplines, particularly in biology and physics. These concepts are instrumental in modeling phenomena such as population dynamics and radioactive decay.
Population Dynamics – The growth of biological populations can often be described as exponential, with the rate of increase in a population being proportional to its current size. This concept is crucial for ecologists and biologists in predicting changes in species populations, understanding ecosystem dynamics, and managing wildlife reserves.
Radioactive Decay – In physics, the decay of radioactive substances is another poignant example of exponential decay. The quantity of a radioactive material decreases over time at a rate that depends on its current amount, leading to a predictable pattern of decay. This principle is foundational in fields such as nuclear physics, radiometric dating, and the management of nuclear waste.
The Backbone of Computing and Digital Data
In the digital realm, exponents are integral to the architecture of computing and the representation of data. The binary system, which is the foundation of all computer processes, relies heavily on powers of two. This system simplifies the representation of large data values and the calculation of storage capacities, making it easier for users to understand and for systems to process vast amounts of information. Furthermore, in the development of algorithms for tasks like sorting, searching, and encrypting data, the efficiency and speed of these processes are often described in terms related to exponents, highlighting their importance in optimizing technology for everyday use.
The Underlying Influence of Exponents
These examples-ranging from the way our savings grow, through the natural processes of growth and decay, to the very essence of computing and digital information-illustrate the profound impact of exponents on our daily lives. By enabling us to manage and understand large numbers, rates of change, and data volumes, exponents facilitate a deeper comprehension and more effective handling of complex phenomena. Their application across diverse fields underscores not only their mathematical beauty but also their practical utility, demonstrating how fundamental mathematical concepts are to navigating and enhancing our modern world.