Exponent Division Worksheets

About These 15 Worksheets

These worksheets will help enhance student understanding and proficiency in manipulating mathematical expressions that involve the division of exponents. These worksheets contain a variety of exercises that require students to apply the rules for dividing powers with the same base, which fundamentally involves subtracting exponents. By engaging with these worksheets, students build a stronger grasp of the principles and applications of exponents in arithmetic and algebra.

The diverse types of exercises ensure that students not only learn the rules but also understand their application in various contexts, thereby promoting a deeper and more integrated understanding of exponents and their significance in mathematics and beyond.

The various types of exercises found on Exponent Division Worksheets can range from straightforward numerical division to more complex problems involving variables and algebraic expressions. Here’s an overview of the different kinds of exercises that may be featured:

Numerical and Variable Problems

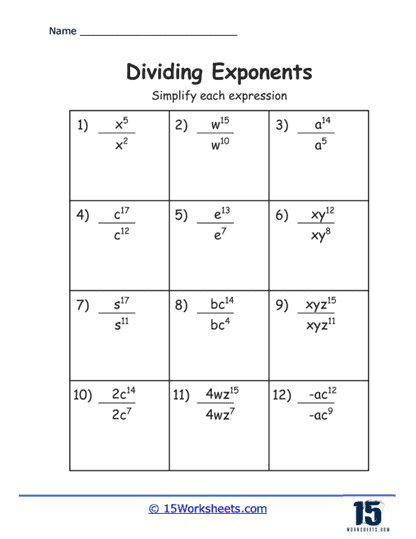
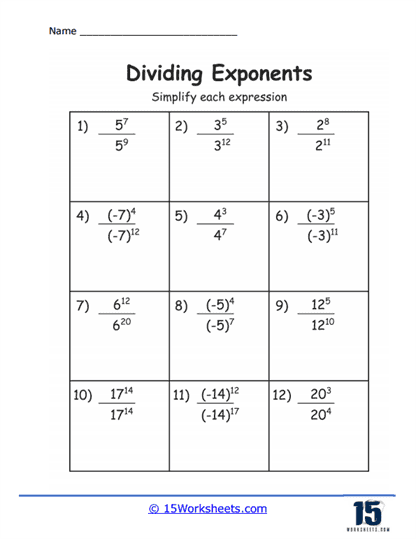
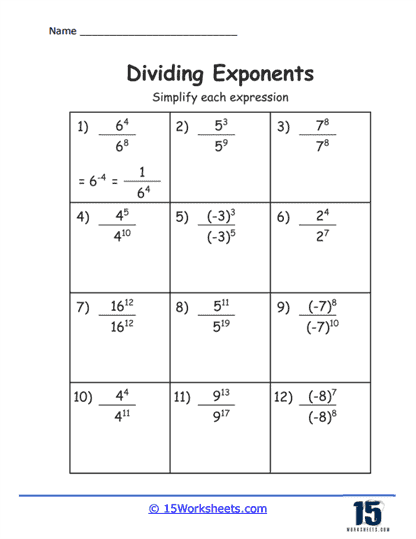
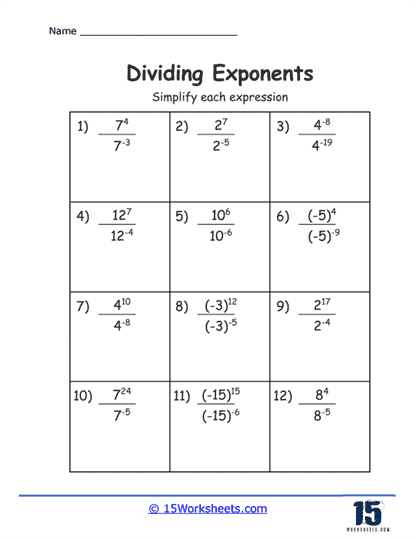
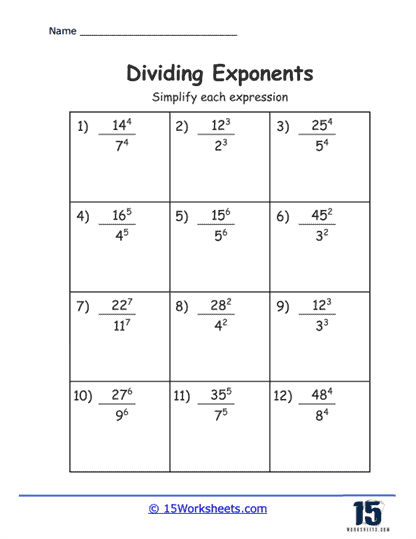
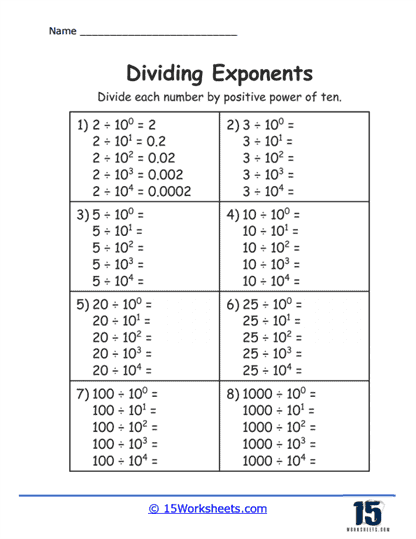
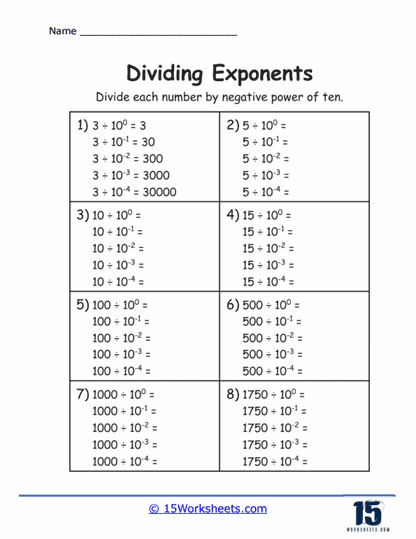
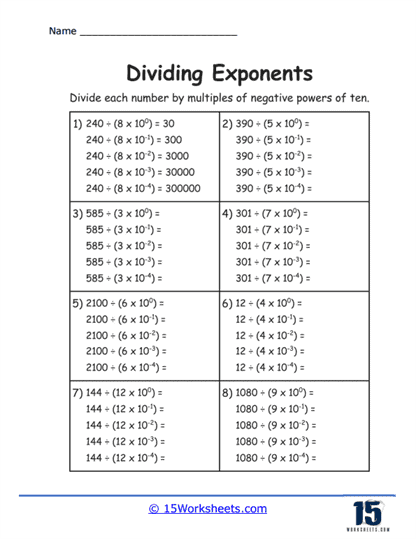
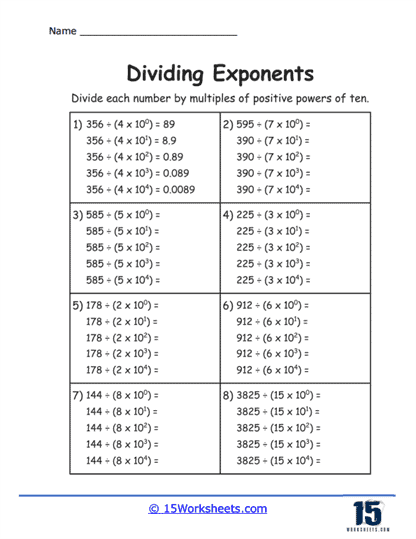
These are the most basic types of problems on such worksheets, where students are presented with two numbers raised to a power. The task is to divide these numbers and simplify the expression according to the rule of exponents that states when you divide powers with the same base, you subtract the exponents.

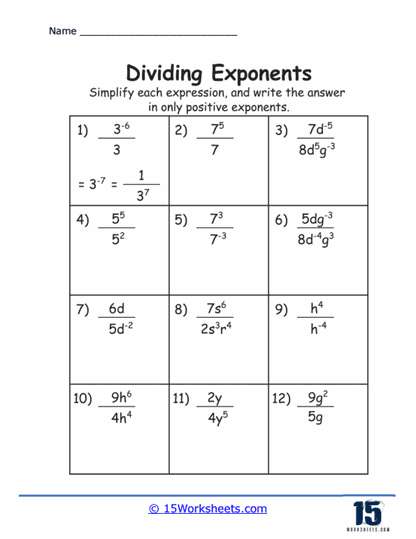
A step up in difficulty, these exercises include variables alongside integers, all raised to an exponent. Students must simplify the expression using the same principles of exponent division. This involves not only the numerical subtraction of exponents but also understanding how variables behave under the laws of exponents.

Missing Exponent and Comparative Problems

In these problems, one of the exponents is typically unknown. The student’s task is to find the value of this unknown exponent. This requires a deeper understanding of the relationship between the base and the exponent, and how division affects this relationship.

These problems ask students to compare two exponential expressions after division to determine which is larger or if they are equal. It helps in reinforcing the understanding of the magnitude of numbers in exponential form.

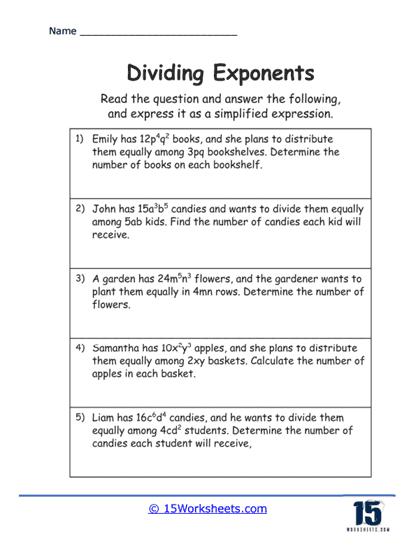
Word Problems

Word problems contextualize exponent division in real-life situations, which can help students understand where this type of math can be applied outside of the classroom. The student must translate the written problem into an algebraic expression and then solve it, thus practicing their analytical and mathematical skills simultaneously.

Fractional Exponents

These are advanced problems that introduce the concept of roots as exponents written in fractional form. Division of such terms requires students to apply both the rules of exponents and an understanding of radicals.

Some worksheets may include problems where students need to solve for a variable within an equation that involves the division of exponents. This combines the concept of exponent division with the techniques of solving equations, thereby challenging the student to use multiple mathematical principles at once.

The Benefits Of These Worksheets

Practicing with these worksheets helps students improve their understanding of exponents in several ways:

Strengthening Foundation

Exponents are a fundamental concept in mathematics that appear in various forms as students advance through their studies. Proficiency in dividing exponents lays the groundwork for higher mathematics, including calculus and complex number theory. Exponent division requires attention to detail. Students must be careful in applying the rules accurately, and consistent practice on these worksheets can help in minimizing errors and developing precision.

Building Problem-Solving Skills

By solving different types of exponent division problems, students enhance their overall problem-solving abilities. They learn to approach a problem from multiple angles and to apply a systematic method to reach the solution.

These worksheets contain problems that mimic real-world scenarios, helping students understand the practical applications of exponents. This can lead to a greater interest in STEM fields where such mathematical principles are regularly applied.

A solid grasp of exponent rules is crucial for tackling advanced topics in mathematics and sciences. These worksheets prepare students by ensuring they are comfortable with exponent division before they encounter more complex applications, such as exponential growth and decay models.

How Do You Do Division with Exponents?

Dividing exponents is a fundamental aspect of algebra that involves manipulating powers of numbers. The approach to dividing exponents depends on whether the bases of the exponents are the same or different.

Dividing Exponents with the Same Base

When you divide exponents with the same base, you use the Quotient of Powers Rule. This rule states that to divide two exponents with the same base, you keep the base the same and subtract the exponent of the denominator from the exponent of the numerator.

Here’s the general formula:

a^m ÷ aⁿ = a ^{(m – n)}

Where a is the base and m and n are the exponents.

Here’s a detailed explanation of the steps:

Step #1 – Write down the problem

Begin by writing down the expression with both terms. Ensure that the bases are the same.

Step #2 – Subtract the exponents

Subtract the exponent of the divisor (the number you’re dividing by) from the exponent of the dividend (the number that is being divided).

Step #3 – Simplify the expression

Write the result as the base raised to the difference of the two exponents.

Example with the Same Base

2⁸ ÷ 2³

According to the Quotient of Powers Rule

2⁸ ÷ 2³ = 2^{(8 – 3)} = 2⁽⁵⁾

Dividing Exponents with Different Bases

When the bases of the exponents are different, and the exponents are the same, you can use the Division of Powers Rule to simplify the expression. This rule states that to divide two exponents with different bases but the same exponent, you divide the bases and keep the exponent the same.

Here’s the general formula:

a^m ÷ b^m = (a ÷ b)^m

However, when the exponents are also different, there’s no direct rule that applies, and you must treat each term individually. If possible, simplify the terms to the same base and then apply the Quotient of Powers Rule. If this isn’t possible, you may need to evaluate each term separately and then perform the division.

Example with Different Bases, Same Exponent

8³ ÷ 4³

Since the exponents are the same, we can divide the bases

8³ ÷ 4³ = (8 ÷ 4)³

= (2)³ or 2 x 2 x 2 = 8.

Example with Different Bases, Different Exponents

16⁴ ÷ 2⁵

First, we see if we can write each term with the same base. Since 16 is a power of 2 (since 16 = 2⁴), we can rewrite 16⁴ as (2⁴)⁴.

(2⁴)⁴ ÷ 2⁵

Apply the Power of a Power Rule for exponents (which states that (a^m)ⁿ = a ^mn

2¹⁶ ÷ 2⁵

Now that we have the same base, we can subtract the exponents:

2^{(16 – 5)} = 2¹¹

The strategy for dividing exponents will differ depending on whether the bases or the exponents are the same or different. Using the quotient rule, you can simplify expressions with the same base, and with a bit of algebraic manipulation, even those with different bases can be simplified under certain conditions.