Operations with Exponents Worksheets

About These 15 Worksheets

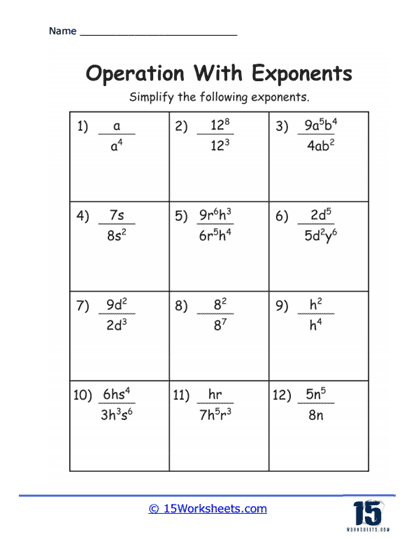
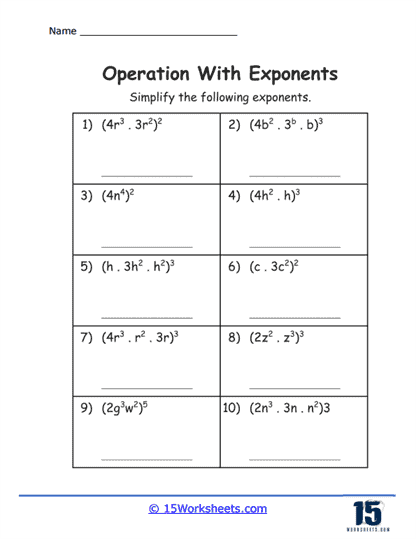
These worksheets were designed to enhance students’ understanding and proficiency in handling mathematical expressions involving exponents. Exponents, also known as powers, represent a fundamental concept in mathematics where a number is multiplied by itself a specified number of times. The expression aⁿ, for example, signifies that the base a is multiplied by itself n times, where n is the exponent. These worksheets cover a range of exercises aimed at developing students’ abilities to work with exponents effectively. Engaging with these exercises not only reinforces the mechanics of using exponents but also deepens the conceptual understanding of exponential relationships, essential for advanced mathematical studies and real-world applications.

The worksheets encompass several types of exercises, each targeting a specific skill set related to exponents. Below are the different types of exercises one might encounter on these worksheets:

Basic Exponent Rules – Exercises in this category familiarize students with the fundamental rules of exponents, such as the product rule (a^m x aⁿ = a^{m + n}), the quotient rule (a^m / aⁿ = a^{m – n}), and the power of a power rule ((a^m)ⁿ = a^mn). These problems help students internalize how exponents behave during multiplication, division, and exponentiation of powers.

Negative Exponents – These exercises introduce the concept of negative exponents, emphasizing that a^-n = 1 / aⁿ. Students practice converting expressions with negative exponents to their positive counterparts and vice versa, deepening their understanding of the reciprocal nature implied by negative exponents.

Zero Exponent – Problems in this section underscore the principle that any nonzero number raised to the zero power equals one (a⁰ = 1). Exercises often involve simplifying expressions to illustrate how different exponent rules apply when the exponent is zero.

Fractional Exponents – Students practice converting between radical expressions and expressions with fractional exponents, reinforcing the versatility of exponential notation.

Scientific Notation – Worksheets include exercises on expressing large or small numbers in scientific notation, where a number is represented as the product of a base (between 1 and 10) and an exponent of 10. These problems enhance students’ ability to handle very large or very small numbers efficiently, a skill crucial in science and engineering.

Exponential Equations – Solving equations where the variable appears in an exponent tests and strengthens students’ grasp of logarithms as the inverse operation of exponentiation. These exercises often require applying logarithms to both sides of an equation to isolate the variable.

Exponential Growth and Decay – These real-world application problems involve formulas for exponential growth and decay, teaching students how exponents model phenomena such as population growth, radioactive decay, and compound interest. Through these exercises, students learn to apply their knowledge of exponents to understand and predict the behavior of systems over time.

How Are Exponent Operations Used Every Day?

Math operations involving exponents find extensive application across a broad spectrum of real-world scenarios. From calculating interest in finance to understanding the decay of radioactive substances in physics, the principles governing exponents are pivotal. This discussion delves into the practical uses of exponents across various fields, emphasizing their versatility and critical role in solving complex problems.

Finance and Economics – In the realm of finance, exponents play a critical role in understanding how investments grow over time through the concept of compound interest. This principle allows individuals and institutions to calculate the future value of investments or loans, considering the effect of accumulating interest. By applying exponential operations, financial experts can forecast investment growth, guide savings strategies, and make informed decisions regarding loans and mortgages.

Population Dynamics – Exponents are also key in modeling population growth or decline. They help biologists and environmental scientists predict future population sizes based on current trends. Whether it’s understanding how a species proliferates under ideal conditions or assessing the impact of factors leading to population decrease, exponential models provide insights that are crucial for conservation efforts, urban planning, and resource management.

Physics and Chemistry – In the sciences, exponents are fundamental in explaining natural processes such as radioactive decay. They allow scientists to determine the rate at which substances lose their radioactivity over time, which is essential in fields like nuclear medicine, archaeological dating, and nuclear energy management. Additionally, exponential decay models help chemists and physicists understand and predict the behavior of various phenomena at the atomic and molecular levels.

Thermodynamics – The cooling or heating of objects over time, as they adjust to the temperature of their surroundings, is another area where exponents find application. By modeling temperature changes exponentially, engineers and scientists can design more efficient cooling systems, study the thermal properties of materials, and improve energy conservation methods in buildings and electronic devices.

Acoustics and Electronics – The exponential decrease in sound intensity with distance and the discharge rate of capacitors in electronic circuits are critical concepts in acoustics and electronics, respectively. These principles guide the design of soundproofing materials, audio technology, and the development of electronic components that power our daily lives, from smartphones to computers.

Computer Science – The concept of exponential growth is evident in the evolution of computing power and the complexity of data processing algorithms. This principle has driven technological advancements, enabling the development of faster, more efficient computational systems that power everything from consumer electronics to advanced research in artificial intelligence and machine learning.

Epidemiology – Understanding the spread of infectious diseases through exponential models is crucial in epidemiology. It aids in predicting the course of outbreaks and implementing effective public health measures. By analyzing how diseases spread rapidly in the initial stages, health officials can better prepare for and mitigate the impacts of epidemics and pandemics.

These examples highlight the broad applicability of exponents in solving real-world problems and enhancing our understanding of natural and man-made phenomena. Without the direct use of mathematical formulas, it’s clear that exponents are a fundamental tool across various disciplines, enabling professionals to make predictions, understand trends, and develop strategies based on exponential growth and decay patterns.