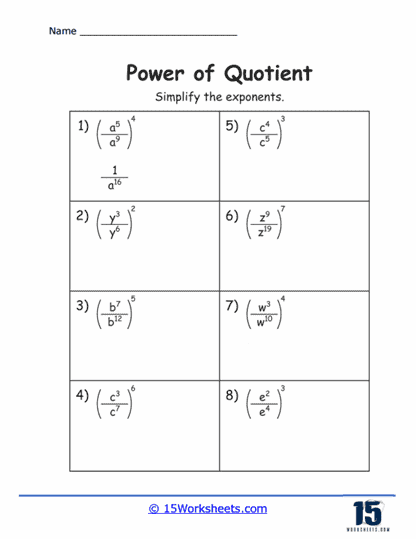
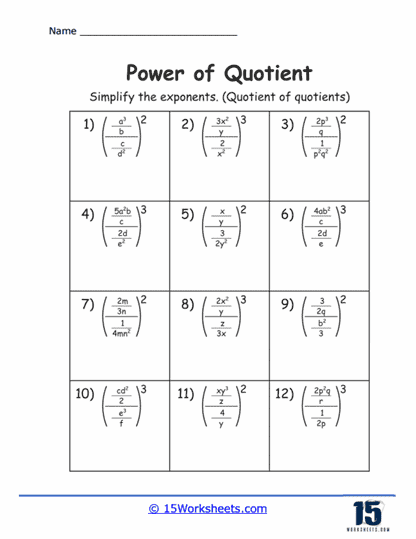
Power of Quotients Worksheets

About These 15 Worksheets

These worksheets will help enhance student mastery of exponents, specifically focusing on the rules and applications related to the division of bases with exponents, known as quotients. These worksheets cater to a variety of learning levels, offering exercises that range from introductory concepts to more complex applications of exponent rules. Through systematic practice, students can deepen their comprehension of how exponents behave in division scenarios, ultimately strengthening their overall mathematical prowess.

At the heart of these worksheets is the concept that when you divide powers with the same base, you can subtract the exponents. This principle is crucial for simplifying expressions and solving equations involving exponents. These worksheets guide students through this rule, demonstrating how it streamlines calculations and aids in the simplification of algebraic expressions.

By engaging with the diverse exercises these worksheets offer, students not only refine their skills in handling exponents but also lay a robust foundation for future mathematical endeavors. The disciplined practice of these principles sharpens their problem-solving capabilities, prepares them for advanced topics, and instills a deep-rooted confidence in their mathematical journey. As such, these worksheets are indispensable tools in the educational arsenal, fostering a comprehensive and profound understanding of exponents and their applications.

Types of Problems

Basic Quotient Exercises – Students start with fundamental problems that require them to apply the rule of subtracting exponents directly. These problems typically involve numerical bases and integer exponents, allowing learners to become familiar with the pattern of reducing exponents when dividing like bases.

Algebraic Expressions – As students progress, exercises incorporate variables along with numerical coefficients. These problems challenge students to apply the power of quotients rule within the context of algebraic expressions, enhancing their ability to manipulate and simplify expressions involving variables.

Word Problems – To bridge the gap between abstract concepts and real-world applications, some worksheets include word problems that require the use of quotient of powers rules. These scenarios might involve exponential growth or decay, financial calculations using compound interest, or other practical applications of exponents.

Comparative Problems – Exercises that ask students to compare two expressions involving exponents and determine their equality or relative size without directly calculating their values encourage a deeper understanding of the properties of exponents.

Mixed Operations – To further solidify understanding, worksheets often feature problems that combine multiplication, division, and sometimes addition and subtraction of powers. These exercises require students to apply a combination of exponent rules, fostering a comprehensive grasp of exponent operations.

The Benefits Of These Worksheets

Reinforcement of Exponent Rules – Regular practice helps students memorize and apply the rules governing the operations with exponents, particularly the quotient rule. This familiarity is crucial for higher-level mathematics, where exponents play a pivotal role. By working with algebraic expressions involving quotients and powers, students improve their ability to manipulate and simplify complex expressions. This skill is invaluable in algebra, calculus, and beyond, where the simplification of expressions is frequently required.

Problem-Solving Abilities – Engaging with word problems and comparative exercises sharpens students’ problem-solving skills. They learn to translate real-world situations into mathematical expressions and to apply mathematical principles to find solutions, fostering critical thinking and analytical skills. Mastery of exponent rules, including those related to quotients, lays a solid foundation for more advanced topics in mathematics. Concepts like logarithms, exponential functions, and complex numbers all require a strong understanding of exponents.

Confidence and Competency – As students become more adept at handling exponents through practice, their confidence in their mathematical abilities increases. This confidence can lead to greater success in mathematics and a more positive attitude towards the subject.

To maximize the benefits of our power of quotients worksheets, teachers and students should approach them with a strategic mindset. Starting with basic exercises and gradually increasing the complexity allows learners to build their skills incrementally. Pairing worksheet practice with interactive activities, discussions, and real-life applications can also enhance engagement and retention of the concepts. Regular review sessions, where students revisit previous exercises, ensure that the knowledge remains fresh and applicable.

What Is The Quotient Property Rule?

The Power of a Quotient Rule is a fundamental principle in the algebra of exponents, which provides a method for simplifying expressions where a quotient (a division of two numbers or expressions) is raised to an exponent. This rule is crucial for both simplifying complex algebraic expressions and solving exponential equations efficiently. Understanding and applying the Power of a Quotient Rule can significantly enhance one’s ability to work with powers and roots in various mathematical contexts.

The Principle of the Power of a Quotient Rule

The rule states that when a quotient is raised to an exponent, you can apply the exponent to both the numerator and the denominator separately. Mathematically, it is expressed as:

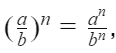
where a and b are any real numbers (with b not equal to zero), and n is an exponent. This means that the power distributes over both the numerator and the denominator of the fraction.

This rule works because of the fundamental principles of exponents, which include the rule that multiplying powers of the same base allows you to add their exponents, and dividing them allows you to subtract the exponents. When you raise a quotient to a power, essentially, you are multiplying the quotient by itself multiple times, which according to exponent rules, means you apply the power to each component of the quotient.

Example – Numerical Bases

Consider the expression (2/3)⁴.

According to the Power of a Quotient Rule, you can apply the exponent of 4 to both the numerator 2 and the denominator 3 separately, which simplifies the expression to:

2⁴ / 3⁴

Calculating each part gives us – 2⁴ = 16 and 3⁴ = 81

This tells us that (2/3)⁴ = 16/81

This example demonstrates how the rule simplifies the expression into a more manageable form, especially useful when dealing with larger exponents or more complex numbers.

When is the Quotient Property of Exponents Used In Real Life?

This property allows for the simplification of expressions where one power is divided by another of the same base, has practical applications in various real-life scenarios. While the abstract mathematical principle might seem distant from daily concerns, its applications permeate several fields, including finance, computer science, engineering, and science. Understanding how this property is used can illuminate the relevance of seemingly esoteric mathematical rules in practical contexts.

Finance and Investment Calculations

In finance, the Quotient Property of Exponents can be used to calculate compound interest rates over different periods or to adjust financial models for inflation or deflation over time. For example, when comparing the effective annual rates of different investment options, financial analysts might use the quotient property to simplify the expressions for easier comparison and decision-making.

Computing and Data Storage

In the realm of computer science, especially in data storage and processing, the Quotient Property is used to calculate file sizes, memory allocation, and data transfer rates. When optimizing algorithms or computing operations that involve exponential growth of data (such as in databases or network traffic analysis), this property helps in simplifying the calculations, leading to more efficient data management and resource allocation.

Engineering and Physics

Engineers and physicists often deal with scales and measurements that span vast exponent ranges, from the incredibly small to the astronomically large. The Quotient Property of Exponents aids in converting between units of measurement, especially when dealing with quantities measured in powers of ten (such as in the metric system). For example, converting between gigawatts and megawatts, or nanometers and micrometers, involves simplifying expressions using the Quotient Property.

Scientific Concentrations and Dilutions

In chemistry and biology, when working with solutions’ concentrations or dilutions, the Quotient Property is applied to calculate the final concentration of a solution after it has been diluted or concentrated. This involves mathematical operations that directly utilize the principles behind the Quotient Property, especially when the concentration changes involve exponential factors.

Logarithmic Scales

Logarithmic scales, which are used in measuring the intensity of earthquakes (Richter scale), the loudness of sound (decibels), and acidity or alkalinity (pH levels), inherently apply the Quotient Property of Exponents. These scales transform the vast range of possible values into a more manageable form, using the principles of exponents and their quotients to represent large variations in a compressed, easily understandable format.