Exponents with Fractional Bases Worksheets
About These 15 Worksheets
Exponents with Fractional Bases Worksheets are educational resources designed to help students understand and master the concept of raising numbers to fractional powers. These worksheets involve exercises that require the application of exponents rules to fractional bases, reinforcing students’ understanding of both exponents and fractions. Engaging with these worksheets enables students to explore the complexities of exponents in a structured manner, improving their mathematical skills and confidence.
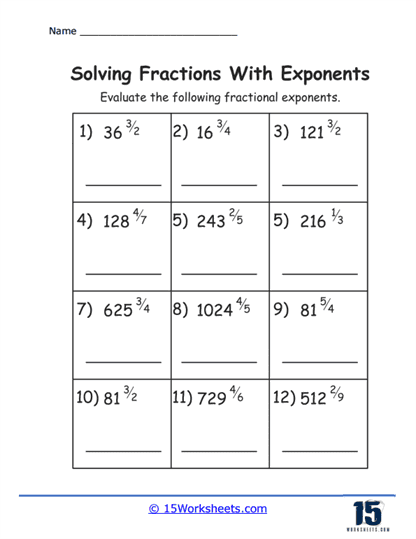
Students must apply the rule that a m/n = n √ am, where a is the base, m is the numerator of the fraction, and n is the denominator. This rule is fundamental for understanding how to manipulate expressions with fractional exponents. Simplification exercises help students become familiar with converting between radical and exponent forms, a crucial skill in algebra and calculus.
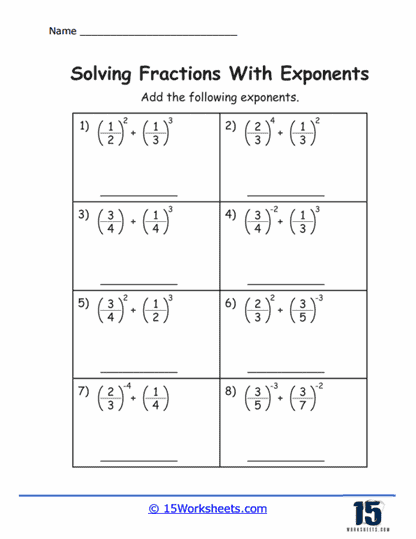
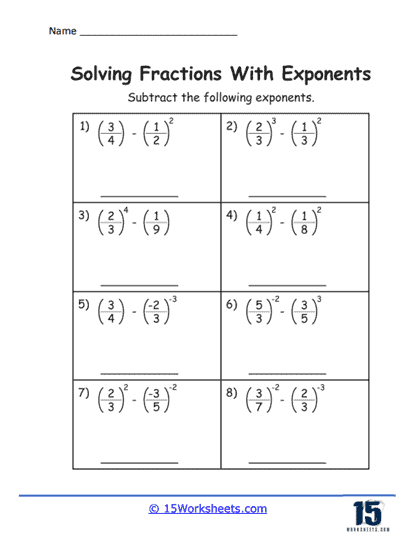
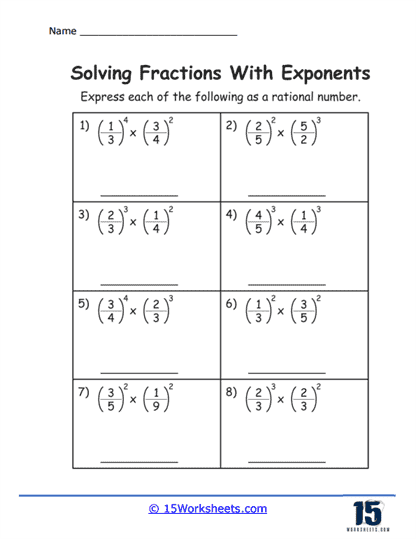
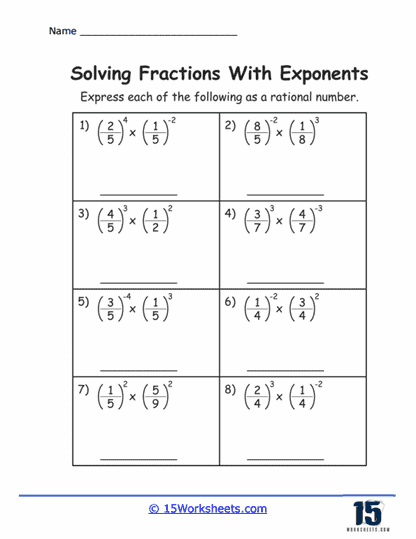
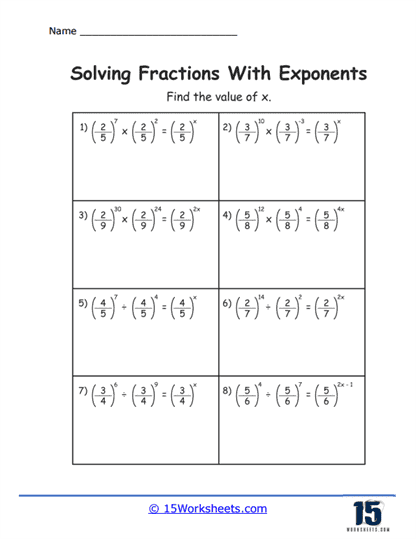
Another exercise type involves the application of the laws of exponents, such as the product rule (am x an = am + n), the quotient rule (am / an = am – n), and the power of a power rule ((am)n = am x n). When the base is fractional, these rules test students’ ability to handle multiple layers of complexity in algebraic expressions. For instance, students might encounter exercises where they must multiply or divide numbers with fractional exponents, requiring them to add or subtract the exponents accordingly.
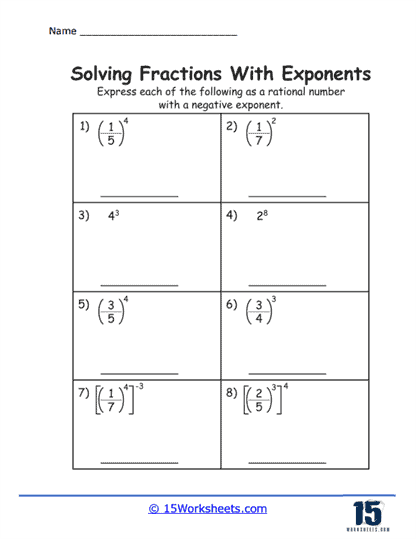
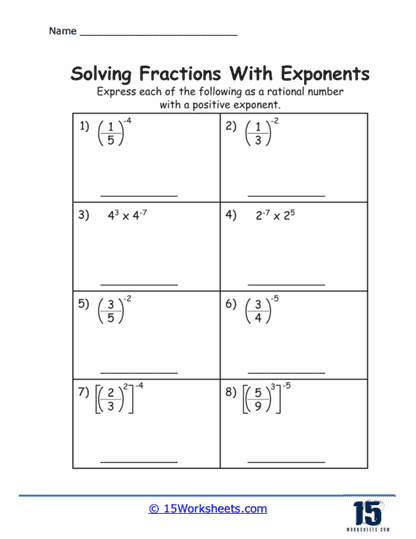
Worksheets also include exercises that combine fractional bases with negative exponents. These exercises are particularly valuable for teaching students about the reciprocal nature of negative exponents. Working through these problems, students gain a deeper understanding of how negative exponents affect fractional bases, further expanding their repertoire of mathematical tools.
Word problems represent another important category of exercises. These problems contextualize fractional exponents in real-world scenarios, requiring students to apply their knowledge to solve practical problems. For example, a word problem might involve calculating the decay of a substance using a formula that incorporates a fractional exponent. Such exercises not only enhance students’ understanding of fractional exponents but also improve their problem-solving skills and their ability to apply mathematics in real-life situations.
Practicing with Exponents with Fractional Bases Worksheets offers numerous benefits to students. Firstly, it solidifies their grasp of exponent rules. Regular practice enables students to internalize these rules, making it easier for them to manipulate and simplify expressions involving exponents. This foundational knowledge is crucial for advanced mathematics, including algebra, calculus, and beyond.
These worksheets improve students’ fluency with fractions. Since the exercises involve fractional bases, students must engage with fractions in a more complex setting than simple arithmetic operations. This exposure helps demystify fractions and builds confidence in handling them within various mathematical contexts.
Working with these worksheets enhances students’ algebraic thinking. Algebra involves finding unknowns and working with abstract symbols, and exercises with fractional exponents require a level of abstract thinking and manipulation of symbols. By practicing these skills, students become more adept at algebraic reasoning, which is essential for success in higher-level math courses.
These worksheets foster problem-solving skills. Mathematics is not just about knowing formulas and rules; it’s about applying this knowledge to solve problems. Exercises, especially word problems involving fractional exponents, require students to think critically about how to apply what they’ve learned to new situations. This practice is invaluable for developing a problem-solving mindset that is beneficial in academics and real-world scenarios alike.
Engaging with Exponents with Fractional Bases Worksheets builds mathematical resilience. Mathematics can be challenging, and encountering difficult problems is a part of the learning process. By working through complex exercises involving fractional exponents, students learn to persevere through challenges, a skill that is crucial both in and out of the classroom.
How Do You Solve Exponents With Fractional Bases?
Solving exponents with fractional bases involves understanding that a number raised to a fractional exponent is equivalent to taking the root of the number, as indicated by the denominator of the fraction, and then raising the result to the power of the numerator. The general rule is:

where a is the base, m is the numerator of the fraction, and n is the denominator.
Example 1 – Simplifying a Fractional Exponent
Solve – 82/3
Step #1 – Interpret the fractional exponent – Here, 2/3 means we take the cube root of 8 and then square the result.
Step #2 – Calculate the cube root – The cube root of 8 is 2, because 23 = 8.
Step #3 – Square the result – 22 = 4
Solution – 82/3 = 4
Example 2 – Fractional Base with a Fractional Exponent
Solve – (1/27)2/3
Step #1 – Interpret the fractional exponent – Here, 2/3 means we take the cube root of 1/27 and then square the result.
Step #2 – Calculate the cube root – The cube root of 1/27 is 1/3, because (1/3)3 = 1/27.
Step #3 – Square the result – 1/32 = 1/9.
Solution – (1/27)2/3 = 1/9
Example 3 – Negative Fractional Exponent
Solve – 16-3/4
Step #1 – Interpret the negative fractional exponent – Here, -3/4 means we take the fourth root of 16, raise the result to the third power, and then take the reciprocal because the exponent is negative.
Step #2 – Calculate the fourth root – The fourth root of 16 is 2, because 24 = 16.
Step #3 – Raise to the third power – 23 = 8.
Solution – 16-3/4 = 1/8
These examples demonstrate the process of solving expressions with fractional bases and exponents, emphasizing the importance of understanding how to interpret fractional exponents and apply root and exponent operations.