Laws of Exponents Worksheets
About These 15 Worksheets
These worksheets can be used to teach and reinforce the rules governing the operation of exponents in mathematics. These worksheets are essential for helping students navigate the sometimes tricky terrain of exponential expressions, which are fundamental in various fields of math, including algebra, calculus, and beyond. The exercises included in these worksheets cover the full spectrum of exponent rules, ensuring that learners become adept at handling exponential numbers in any mathematical setting.
The worksheets will introduce students to the basic exponent rules – the Product of Powers rule, the Power of a Power rule, the Quotient of Powers rule, the Power of a Product rule, and the Power of a Quotient rule. Each type of exercise aims to instill a different aspect of understanding exponents.
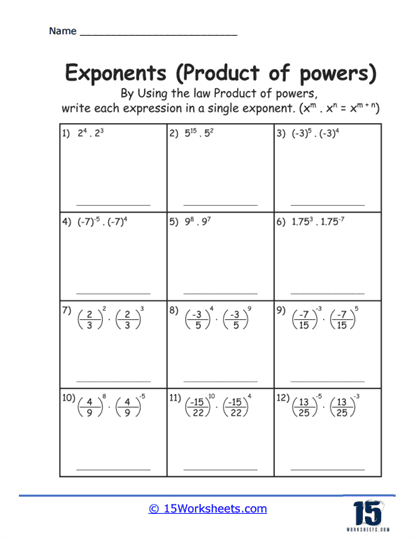
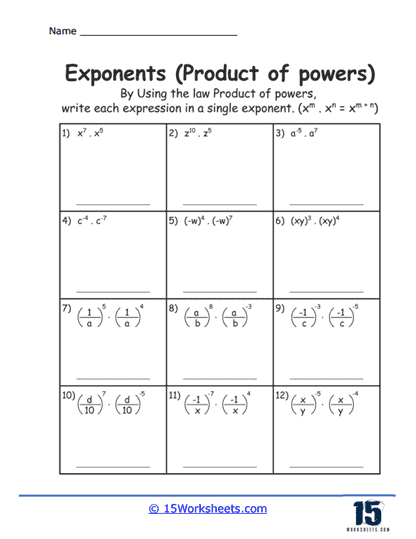
The Product of Powers exercises guide students through the process of multiplying like bases. They learn that when multiplying two exponents with the same base, they must keep the base the same and add the exponents. For example,
am x an = am + n. This rule is pivotal for simplifying expressions and solving equations involving exponents.
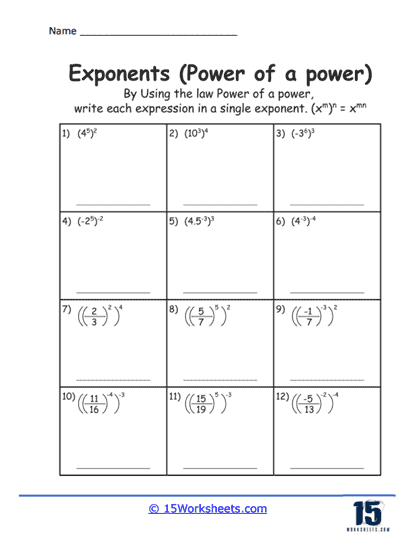
The Power of a Power tasks require students to raise an exponent to another power. Through these exercises, students practice multiplying the exponents. This is often visually represented as (am)n = am x n. Mastering this rule is especially helpful when dealing with complex exponential expressions in higher-level mathematics.
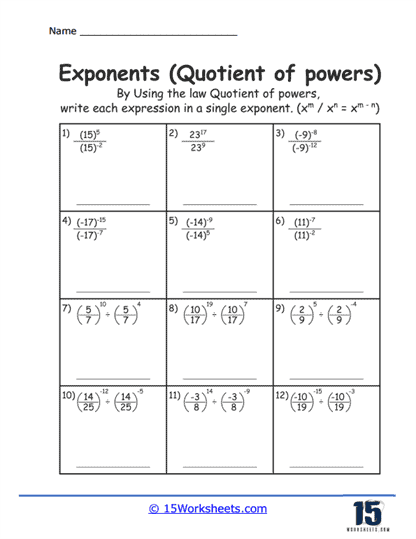
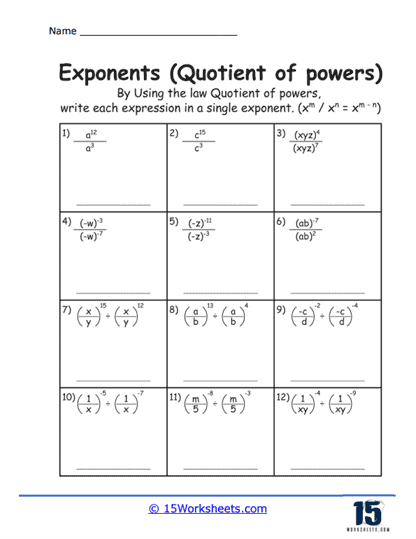
Quotient of Powers problems present students with division scenarios where the bases are the same. Students learn to subtract the exponent in the denominator from the exponent in the numerator, following the rule am ÷ an = am – n. This skill is crucial for simplifying algebraic expressions and solving rational exponential equations.
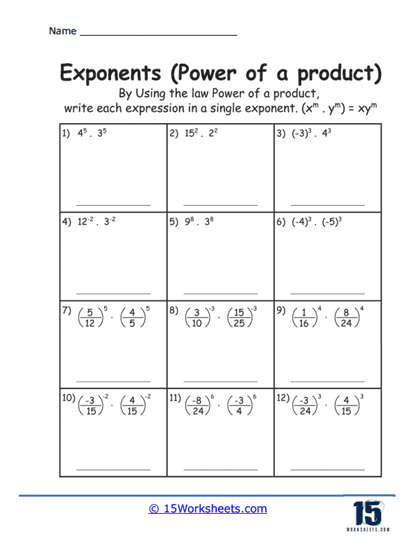
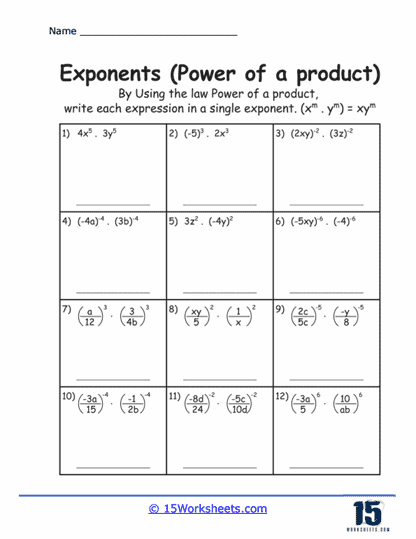
Power of a Product exercises help students understand that when a product is raised to a power, the exponent applies to each factor in the product separately, as in abm = am bm. This reinforces the distributive property over multiplication regarding exponents and lays the groundwork for expanding binomials raised to powers.
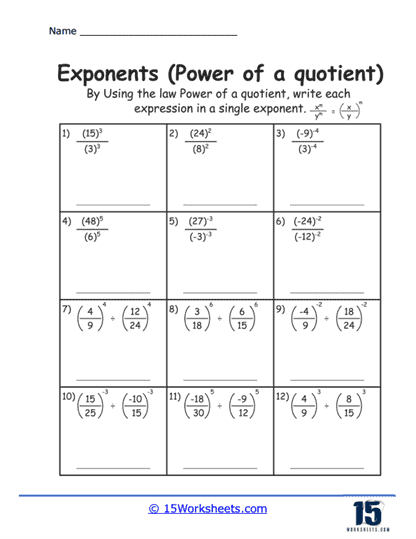
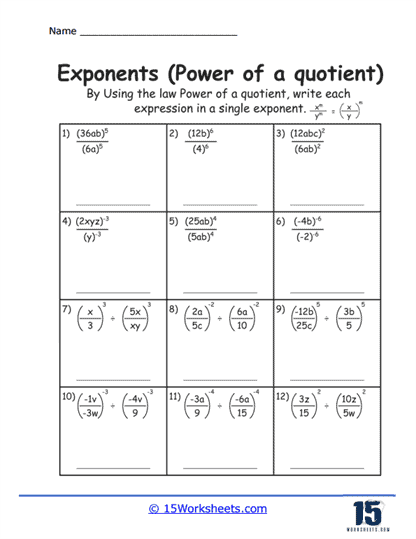
The Power of a Quotient section reinforces the idea that an exponent applies to both the numerator and the denominator of a fraction. The rule abm = (a/b)m = am / bm is fundamental in transforming complex fractions within equations and functions.
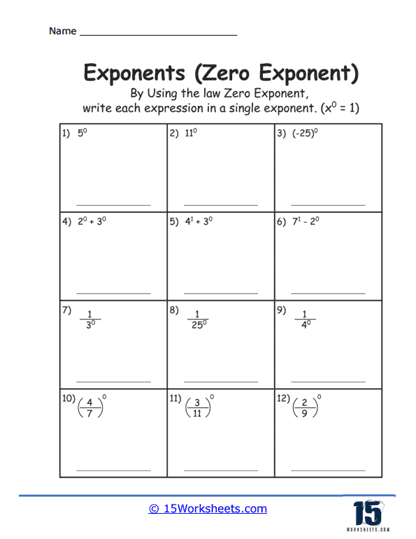
Zero exponent exercises are also common, which teach students that any base raised to the zero power is one, as in
a0 = 1. This concept often initially confuses students, but is pivotal in understanding the identity elements of algebra.
Negative exponents are included to show that a negative exponent indicates the reciprocal of the base raised to the positive opposite of the given power, such as a-m = 1/am. This helps students solve equations where variables are raised to negative exponents and is foundational in understanding polynomial and rational functions.
The Benefits Of These Worksheets
By working through a variety of problems, students learn to recognize patterns and apply the appropriate laws quickly and accurately. This repetitive practice leads to greater proficiency and confidence in manipulating exponents, which translates into better problem-solving skills. As exponents are integral to understanding growth and decay in functions, mastering these worksheets prepares students for more complex mathematical concepts like exponential growth models in biology, compound interest calculations in finance, and logarithmic scales in science.
These worksheets encourage students to engage in self-assessment, as they often include a mix of straightforward problems and more complex challenges that require a deeper understanding of the rules. When students can successfully navigate through harder problems, they gain a sense of accomplishment and are encouraged to tackle even more challenging mathematical concepts.
All of the worksheets come with answer keys, allowing students to check their work immediately. This immediate feedback loop is vital in the learning process, as it enables students to identify and learn from their mistakes on the spot. It also provides an opportunity for self-directed learning, as students can take the initiative to correct their errors and understand the rationale behind the correct solutions.
Which Are the 7 Laws of Exponents?
The 7 Laws of Exponents are mathematical rules that dictate how to handle expressions involving powers. Each law addresses a different aspect of working with exponents, and together they form a foundation for simplifying and manipulating expressions in algebra and higher mathematics. Here is a detailed explanation of each law:
Rule #1 – Product of Powers (Multiplication)
Law – When multiplying two exponents with the same base, you add the exponents.
Formula – am x an = am + n
Example – 32 x 34 = 32 + 4 = 36
Explanation – Since the base is the same (3), you add the exponents (2 and 4) to get a single exponent of 6.
Rule #2 – Quotient of Powers (Division)
Law – When dividing two exponents with the same base, you subtract the exponent of the denominator from the exponent of the numerator.
Formula – am ÷ an = am – n (Assumes a is not equal to 0)
Example – 57 ÷ 53 = 57 – 3 = 54
Explanation – With the same base of 5, subtract the exponent in the denominator (3) from the exponent in the numerator (7) to get the new exponent (4).
Rule #3 – Power of a Power
Law – When raising an exponent to another power, you multiply the exponents.
Formula – (am)n = am x n
Example – (23)4 = 23 x 4 = 212
Explanation – The power outside the parenthesis (4) multiplies with the exponent inside (3), giving you an exponent of 12.
Rule #4 – Power of a Product
Law – When raising a product to a power, the exponent applies to each factor inside the product separately.
Formula – (ab)m = am x bm
Example – (2 x 3)2 = 22 x 32 = 4 x 9 = 36
Explanation – The exponent 2 applies to both 2 and 3, squaring both numbers before multiplying the results.
Rule #5 – Power of a Quotient
Law – When raising a quotient to a power, the exponent applies to both the numerator and the denominator of the fraction.
Formula – (a/b)m = am / bm (Assumes b is not equal to 0)
Example – (4/3)2 = 42 / 32 = 16/9
Explanation – The exponent 2 applies to both 4 and 3, squaring both the numerator and the denominator separately.
Rule #6 – Zero Exponent
Law – Any base raised to the zero power is equal to one.
Formula – a0 = 1 (Assumes a is not equal to 0)
Example – 70 = 1
Explanation – Regardless of the value of the base (as long as it’s not zero), raising it to the power of zero will always result in one.
Rule #7 – Negative Exponent
Law – A negative exponent represents the reciprocal of the base raised to the absolute value of the exponent.
Formula – a-m = 1/am (Assumes a is not equal to 0)
Example – 2-3 = 1/23 = 1/8
Explanation – The negative exponent (-3) on the base 2 indicates that you take the reciprocal of 2 raised to the power of 3.
Understanding and applying these laws are critical in simplifying algebraic expressions and solving equations involving exponents. They are used frequently in various areas of mathematics, science, and engineering, especially where growth processes or compound phenomena are modeled.