Order of Operations with Decimals Worksheets
All About These 15 Worksheets
Order of operations with decimals math worksheets serve as an invaluable educational resource for teaching and reinforcing the proper sequence of solving mathematical expressions that include decimals. By focusing on the application of the rules governing order of operations-commonly remembered through acronyms like PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction)-these worksheets help students build a solid foundation in mathematical reasoning. The inclusion of decimal-based problems adds an additional layer of complexity, challenging students to not only understand the hierarchy of operations but also to manage precision and accuracy when working with decimal values.
These worksheets cater to a wide range of learners, spanning from elementary students just beginning to tackle basic arithmetic with decimals, to middle school students advancing to more intricate calculations. In some cases, even adults revisiting math for personal or professional growth find these worksheets beneficial. The problems are carefully designed to suit different levels of difficulty, ensuring that learners are appropriately challenged without being overwhelmed. By presenting problems that gradually increase in complexity, these worksheets provide opportunities for practice, allowing students to gain confidence and fluency in both conceptual understanding and practical application.
Types of Exercises
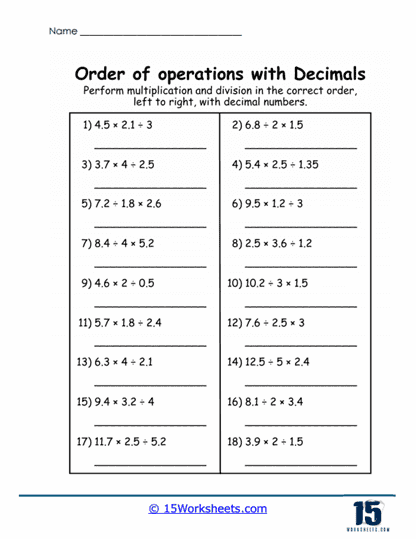
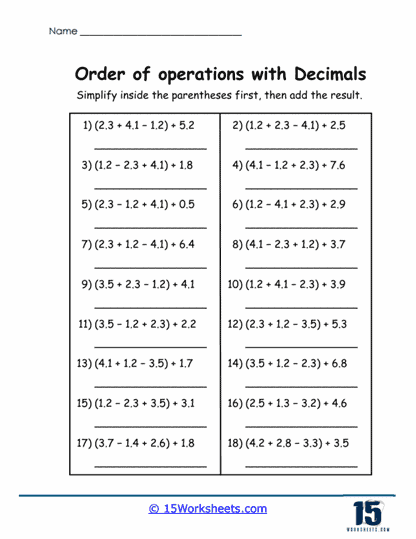
1. Basic Problems with Decimals
The foundational problems in these worksheets focus on simple expressions involving decimals, such as 2.5 + 3.2 x 22.5 + 3.2 x 2. These problems are crafted to involve one or two operations at a time, helping students develop a solid grasp of the order of operations (PEMDAS/BODMAS) without overwhelming complexity.
Purpose and Focus – The primary goal of these basic problems is to reinforce the sequence in which operations should be performed. For example, students learn to multiply 3.2 x 23.2 x 2 first before adding 2.52.5, as dictated by PEMDAS rules. Through repeated practice, students internalize this process, which lays the groundwork for solving more advanced problems later.
Skill Development – These simple problems also focus on fostering accuracy in handling decimal operations. As students practice addition, subtraction, multiplication, and division of decimal numbers, they become more comfortable with decimal placement and its impact on the final answer. This stage is essential for building confidence in working with decimals in real-world contexts.
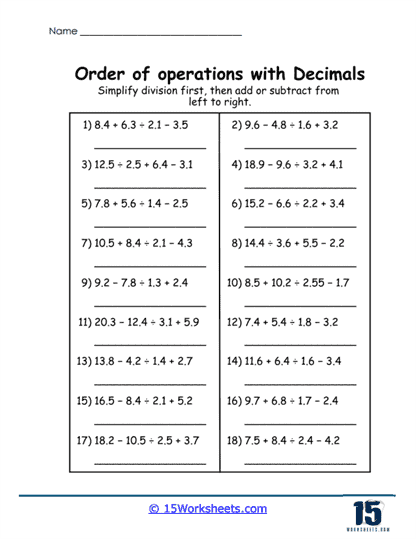
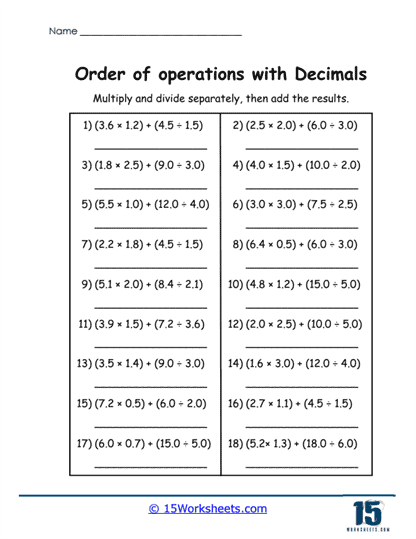
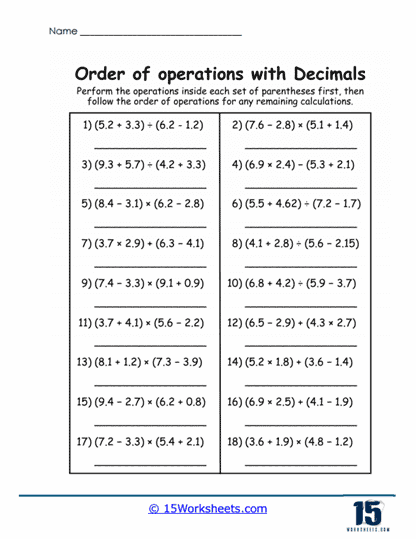
2. Multi-Step Problems
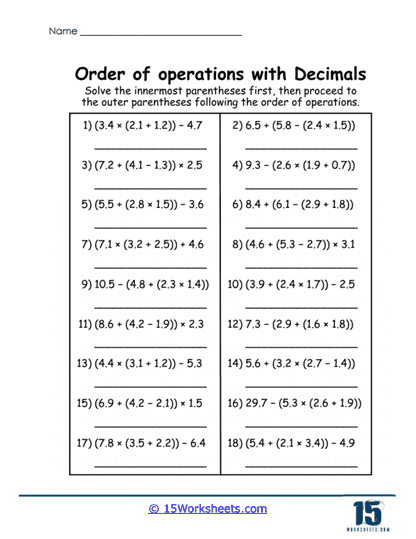
The next level of difficulty introduces problems that combine three or more operations, such as 3.6 x (2.1 + 1.5) – 4.83.6 x (2.1 + 1.5) – 4.8. These problems require students to carefully follow the order of operations, ensuring each step is completed correctly while maintaining precision in decimal calculations.
Challenges and Benefits – Multi-step problems present a higher level of complexity, pushing students to stay organized and methodical. The inclusion of parentheses and multiple operations within a single problem emphasizes the importance of following PEMDAS rules. Missteps in sequencing or decimal placement can lead to incorrect answers, so attention to detail is critical.
Practical Application – These problems help bridge the gap between theoretical understanding and practical problem-solving skills. They encourage students to think critically and approach problems systematically, skills that are valuable in advanced mathematics and everyday situations involving multiple numerical operations.
3. Word Problems
Word problems are an integral component of these worksheets, presenting real-world scenarios where the order of operations must be applied. For example, a problem might state: “A store has a sale where all items are reduced by $1.50. If you buy 3 items priced at $4.25, $6.75, and $3.80, calculate the total cost after the discount.”
Enhancing Comprehension – By framing mathematical concepts within practical situations, word problems help students see the relevance of math in everyday life. These problems also require students to translate verbal information into mathematical expressions, strengthening their ability to interpret and process data.
Multi-Skill Integration – Word problems combine reading comprehension with mathematical problem-solving. Students must carefully read and understand the scenario, identify the relevant operations, and then solve the problem accurately. This integrated approach ensures a deeper understanding and prepares students for standardized tests and real-world tasks.
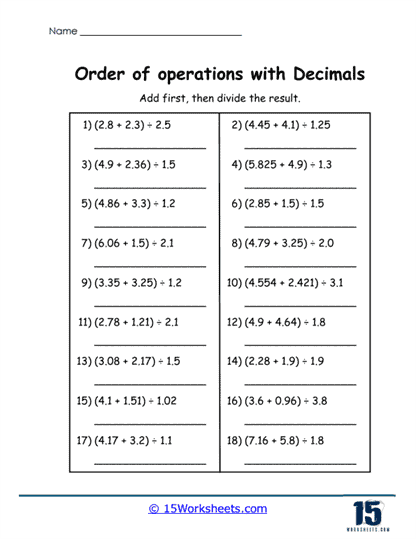
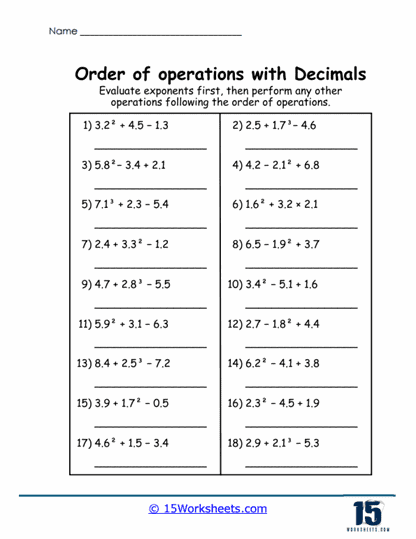
4. Advanced Problems
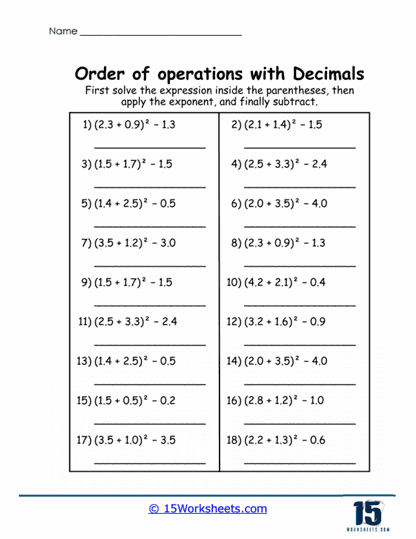
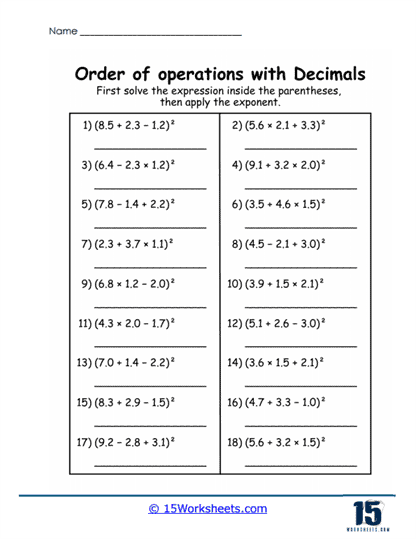
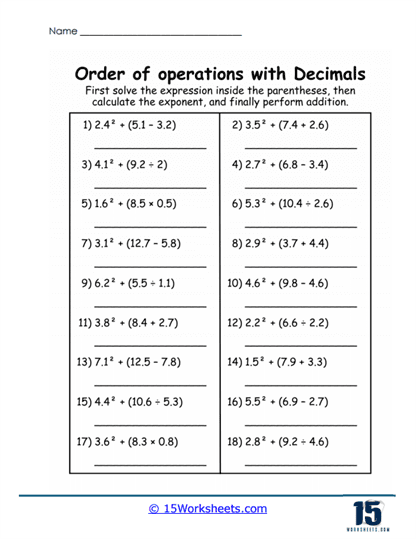
For students seeking a challenge or requiring advanced practice, these worksheets include problems with greater complexity. Such problems may feature exponents, nested parentheses, and intricate decimal values. For example, students might solve (2.4 + 3.2<sup>2</sup>) ÷ 1.6 or ((1.2 x 4.8) – 3.5) + 2.1.
Critical Thinking and Analysis – Advanced problems demand a higher level of critical thinking. Students must not only recall PEMDAS rules but also apply them across multiple layers of operations. The inclusion of exponents and nested parentheses tests their ability to manage hierarchies of operations effectively.
Preparation for Advanced Topics – By solving these problems, students gain exposure to more sophisticated mathematical concepts. This preparation is particularly valuable for those progressing to algebra, calculus, or science subjects where complex computations are common.
5. Error Analysis
Error analysis problems are unique in that they present pre-solved expressions with intentional mistakes, such as 2.5 + 3.2 x 2 = 11.4. Students are tasked with identifying and correcting the errors, explaining why the original solution was incorrect.
Building Analytical Skills – This type of exercise encourages students to think critically and examine problems from a different perspective. Rather than simply solving an expression, they must analyze each step to identify where the error occurred and why it led to an incorrect result.
Encouraging Metacognition – Error analysis fosters metacognitive skills by prompting students to reflect on their own problem-solving processes. This approach not only improves their ability to spot mistakes but also enhances their overall mathematical reasoning and accuracy.
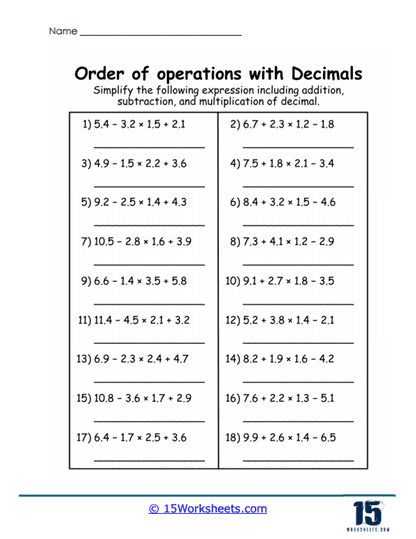
6. Mixed Operations and Decimals
In addition to focusing exclusively on decimals, some worksheets incorporate mixed operations involving fractions, whole numbers, and decimals. These problems are designed to diversify the practice experience and further challenge students.
Diverse Problem Types – By combining different numerical formats, these problems expose students to a broader range of scenarios. For instance, a problem might require students to add a fraction to a decimal or multiply a whole number by a decimal. This variety keeps practice engaging and helps students develop adaptability.
Preparation for Real-World Math – Mixed-format problems are particularly useful in preparing students for real-life situations where numbers often appear in different forms. For example, calculating a bill or balancing a budget may involve working with a combination of whole numbers, decimals, and fractions. Mastery of these problems ensures readiness for such tasks.