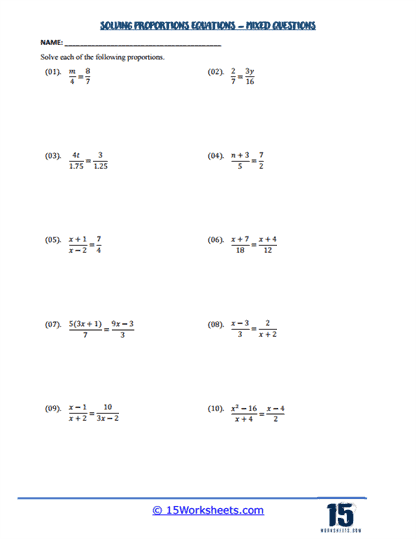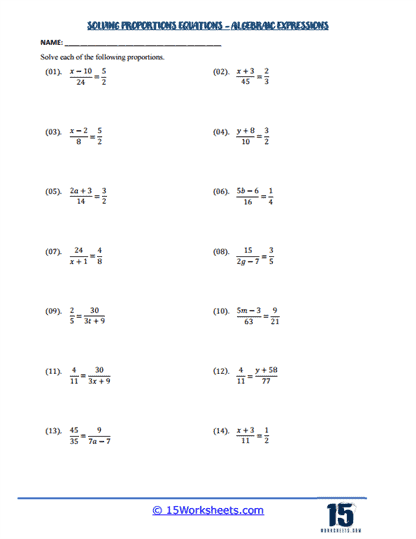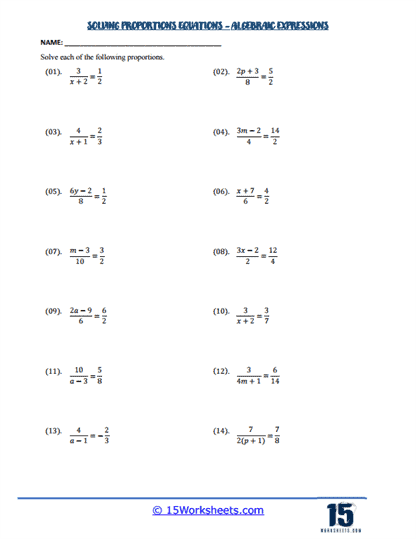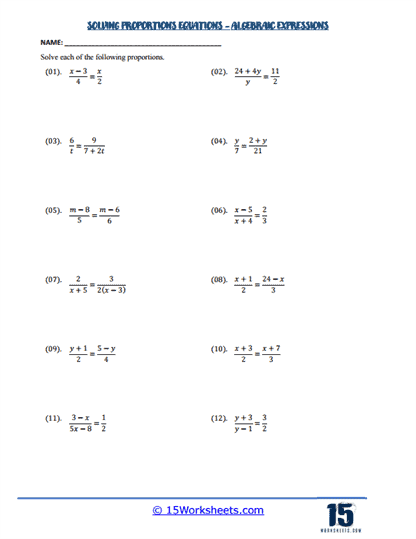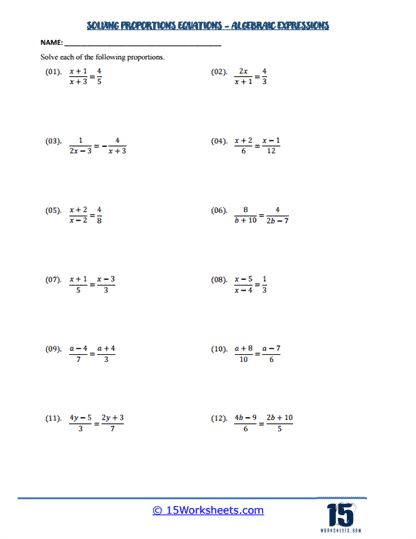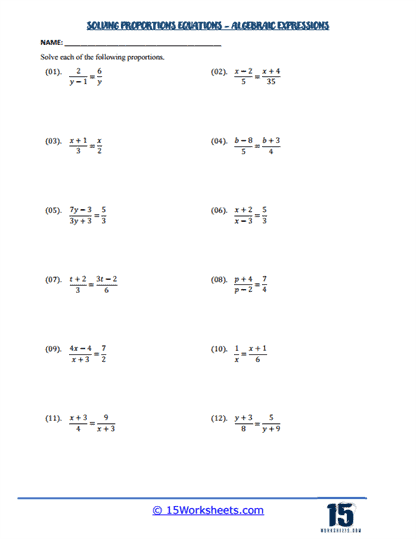Solving Proportion Equations Worksheets
About These 15 Worksheets
These worksheets will help students understand and apply the concept of proportions, a fundamental aspect of mathematics. These worksheets cater to students from grade 6 through high school and cover a wide range of proportion-related topics. They are designed to enhance students’ skills in solving equations that express the equality of two ratios, using methods such as cross-multiplication and inverse operations. Let’s delve into the various types of problems you might encounter on these worksheets and the mathematical skills they help develop, as well as their real-world applications.
Basic Proportion Problems
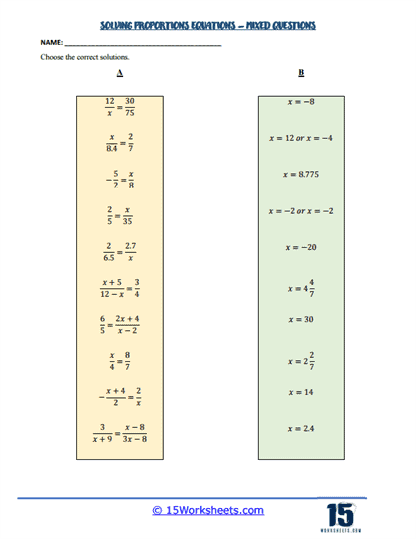
One of the foundational elements of these worksheets is solving basic proportion problems. These exercises often present students with two ratios set equal to each other, such as a/b = c/d, and require them to solve for one unknown variable. For instance, if given x/4 = 3/12, students would cross-multiply to find x = 1. This exercise teaches students the cross-multiplication method, a critical technique for solving proportions. It reinforces the understanding that in a proportion, the product of the means equals the product of the extremes.
Proportions with Fractions and Decimals
As students progress, they encounter proportions involving fractions and decimals. These problems require careful attention to detail, as students must handle fractional and decimal values accurately. For example, solving 2.5/x = 7.5/15 involves cross-multiplying and solving for x, which would result in x = 5. These exercises help students become comfortable working with different numerical forms and enhance their precision in mathematical calculations.
Algebraic Proportions
More advanced worksheets include algebraic proportions, where variables are part of the ratios. For instance, students might solve an equation like x+2/5 = 3x/10. Solving these requires students to apply their knowledge of algebraic manipulation alongside proportion-solving techniques. These problems develop students’ ability to work with algebraic expressions and understand how proportions can be applied in algebraic contexts.
Word Problems Involving Proportions
Word problems are a significant component of proportion worksheets, as they help students apply mathematical concepts to real-world scenarios. These problems might involve scenarios such as mixing ingredients in a recipe, calculating distances based on map scales, or determining the cost of items based on unit prices. For example, a problem might state that if 3 pencils cost $1.50, how much would 10 pencils cost? Students would set up the proportion 3/1.5 = 10/x and solve for x to find the total cost. These exercises enhance students’ problem-solving skills and their ability to translate real-world situations into mathematical equations.
Graphical Representation of Proportions
Some worksheets incorporate graphical elements, asking students to determine if a set of data points on a graph represents a proportional relationship. Students might be tasked with plotting points and checking if the line passes through the origin, indicating a proportional relationship. These exercises help students visualize proportions and understand their graphical representation, reinforcing the concept that proportional relationships are linear and pass through the origin.
Constant of Proportionality
Worksheets on proportions often include problems related to finding the constant of proportionality. This involves determining the constant ratio between two quantities that are directly proportional. For example, if given that y = kx, students might be asked to find the value of k given specific values of x and y. Understanding the constant of proportionality is crucial for grasping how changes in one quantity affect another in a proportional relationship.
Real-World Applications of Proportions
Proportions are not just abstract mathematical concepts; they have numerous real-world applications. In everyday life, you might use proportions when cooking, such as adjusting a recipe to serve more or fewer people. For instance, if a recipe for four people requires two cups of flour, you would use a proportion to calculate the amount needed for six people. In business, proportions help in scaling production, determining cost efficiencies, and analyzing market trends. For example, a company might use proportions to calculate the amount of raw material needed to produce a certain number of products.
In the medical field, proportions are vital for calculating correct medication dosages based on a patient’s weight. For example, if a medication dosage is prescribed at 2 mg per kilogram of body weight, a doctor would use a proportion to determine the appropriate dose for a patient weighing 70 kg. This ensures safe and effective treatment.
In construction and engineering, proportions are used to create scale models and drawings, ensuring that every part of a structure is built to the correct dimensions. For example, if a blueprint uses a scale of 1 inch to 10 feet, a builder would use proportions to convert measurements from the blueprint to actual dimensions.