Combining Like Terms Worksheets
About These 15 Worksheets
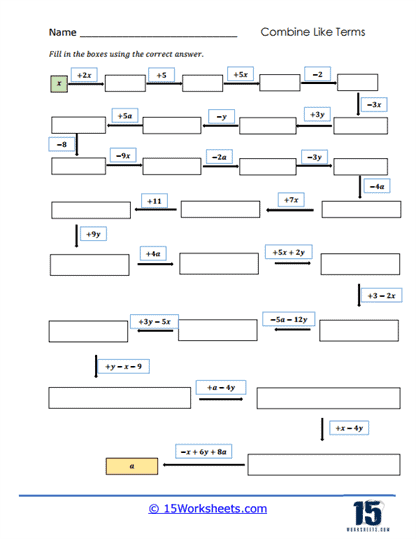
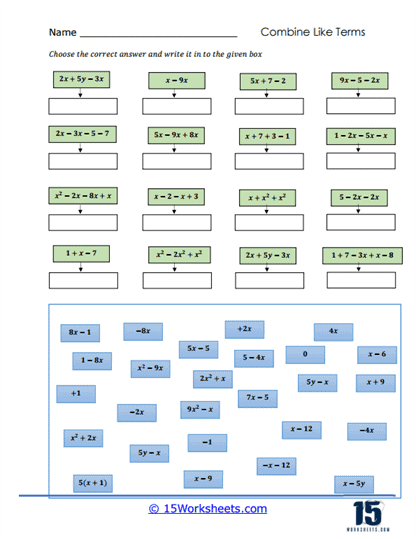
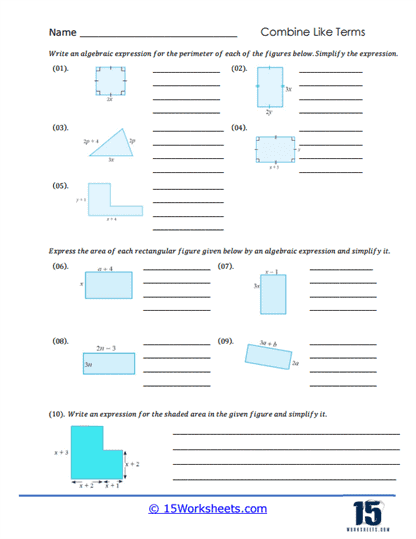
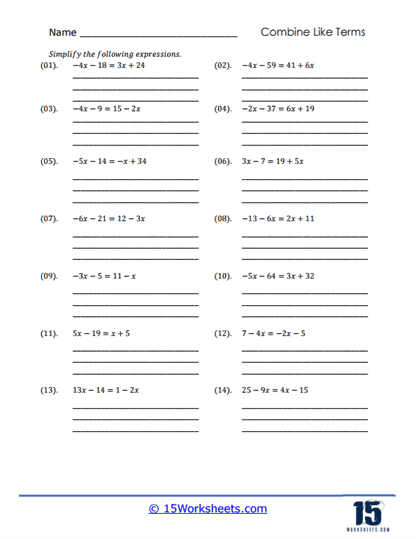
These worksheets will teach students how to simplify algebraic expressions by grouping similar terms. These worksheets focus on building students’ foundational understanding of algebra by helping them recognize and organize terms that share the same variable and exponent. Through a wide variety of problem sets, students develop the skill of identifying like terms, performing basic arithmetic operations on them, and simplifying the expressions to make them more manageable.
One of the first types of exercises on these worksheets involves straightforward algebraic expressions where students are asked to simplify by combining like terms. These problems typically include expressions with terms that have the same variable but different coefficients. For example, an expression like 6x+2x6x+2x would prompt students to combine both terms to produce 8x8x. Through these exercises, students practice adding or subtracting the numerical coefficients of like terms, reinforcing their ability to recognize commonalities in algebraic expressions. This initial step is critical in helping students prepare for more complex algebraic operations.
Other worksheets involve visual or puzzle-style exercises that provide a more interactive approach to learning. In these cases, students may be tasked with matching expressions to their simplified forms or solving for missing terms in a sequence. These exercises are often designed to make the learning process engaging, allowing students to apply their understanding in a way that feels more like solving a puzzle rather than just completing problems. Visual aids, like arrows or grids, guide students through a series of steps to help them arrive at the correct solution, making the learning experience both fun and educational.
There are also worksheets that integrate geometry concepts with algebraic expression simplification. In these exercises, students are given geometric figures such as rectangles, triangles, or complex shapes, and they are required to write and simplify an algebraic expression representing the perimeter or area of the shape. This type of problem allows students to apply their knowledge of combining like terms to real-world scenarios, such as finding the perimeter of a rectangle by combining the lengths of its sides, which are represented by algebraic expressions. The connection between geometry and algebra helps reinforce the importance of algebraic manipulation in practical applications.
In addition to basic expressions and geometry problems, some worksheets focus on more complex expressions with multiple variables. These problems challenge students to recognize which terms can be combined and which cannot, as terms with different variables or exponents must remain separate. For example, in a problem like 5x + 4y + 3x – 2y5x + 4y + 3x – 2y, students must combine the xx-terms and yy-terms separately, resulting in 8x + 2y8x + 2y. This type of problem emphasizes attention to detail and reinforces the need for careful organization in algebraic manipulation.
More advanced worksheets might introduce negative coefficients or subtraction of terms, further complicating the process of combining like terms. In these cases, students must apply their knowledge of integer operations while still focusing on grouping like terms. For instance, simplifying an expression like – 3a + 2a – 4b + b – 3a + 2a – 4b + b requires students to correctly combine both positive and negative terms, resulting in -a – 3b – a – 3b. These problems provide valuable practice in dealing with more challenging algebraic expressions, requiring students to keep track of signs and coefficients carefully.
Another feature found in combining like terms worksheets is the inclusion of equations that need to be simplified before solving. In these problems, students first simplify the algebraic expressions on both sides of the equation by combining like terms. This step reduces the equation to a simpler form, making it easier for students to solve for the unknown variable. These types of exercises not only teach students how to combine like terms but also how to apply this skill in the context of solving equations, which is a crucial part of algebra.
This collection of worksheets will also introduce distributive properties in combination with like terms. In such problems, students first apply the distributive property to expand expressions before combining the resulting like terms. For example, in an expression like 3(x + 2) + 4 x 3(x + 2) + 4x, students must first distribute the 33, resulting in 3x + 6 + 4 x 3x + 6 + 4x, and then combine the xx-terms to get 7x + 67x + 6. This combination of skills helps students see how different algebraic rules work together and reinforces their ability to manipulate expressions efficiently.
As students progress through these worksheets, they encounter more complex and longer expressions with multiple terms. These problems often require several steps to simplify fully, allowing students to practice organizing their work and following a clear, logical sequence of steps. This type of problem reinforces the importance of patience and precision in solving algebraic expressions and prepares students for higher-level algebra courses.