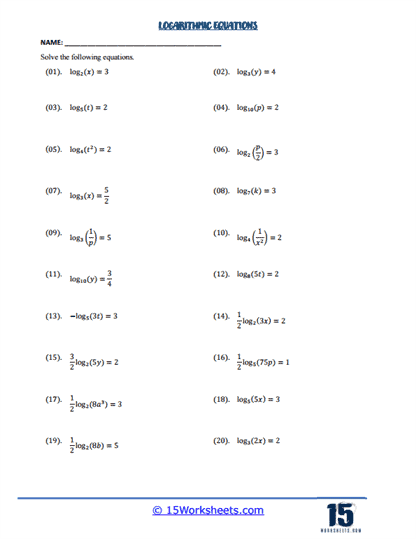Logarithmic Equations Worksheets
About These 15 Worksheets
These worksheets are invaluable tools for teaching students how to solve equations involving logarithms. These worksheets are designed to help students practice and master the various techniques required to manipulate and solve logarithmic equations. By providing a range of problems that gradually increase in complexity, these worksheets guide students from basic logarithmic concepts to more advanced problem-solving skills.
One of the key components you’ll find on these worksheets is the simple logarithmic equation. These problems often involve equations where the logarithm of a single expression equals a constant, such as logb (x) = c. Here, students must apply their knowledge of logarithms and exponents to solve for the variable x. This fundamental skill is crucial because it helps students understand how logarithms relate to their corresponding exponential functions. By repeatedly solving these types of problems, students become comfortable with converting between logarithmic and exponential forms, a foundational skill in algebra and calculus.
Another type of problem commonly found on these worksheets involves equations where students need to solve logarithmic expressions with different bases. For example, a problem might involve logb (x) = logc (y), requiring students to either convert the logarithms to a common base or use the properties of logarithms to manipulate the equation into a solvable form. These problems teach students how to handle logarithms in a more flexible way, showing them how logarithmic properties like the change of base formula can be used to solve equations that might initially seem complex. This type of practice reinforces the understanding that logarithms, regardless of their base, follow consistent rules that can be applied universally.
These worksheets also include problems that involve logarithmic expressions within an equation. For example, you might see equations where logarithms are added, subtracted, or even multiplied, such as logb (x) + logb (y) = c or logb (x) x logb (y) = c. These problems are designed to teach students how to use the properties of logarithms, such as the product, quotient, and power rules, to simplify and solve equations. By working through these problems, students learn to recognize how logarithmic expressions can be combined or separated, and how these manipulations can lead to a solution.
More advanced logarithmic equations worksheets often include problems that combine logarithmic equations with other algebraic techniques. For example, students might encounter problems where they need to solve an equation involving both a logarithmic term and a linear or quadratic term, such as logb (x2) + x = c. These problems require students to integrate their knowledge of logarithms with other areas of algebra, making the process of solving these equations more complex and engaging. This type of practice is crucial for students who are preparing for higher-level math courses, as it helps them develop the ability to solve multi-step problems that involve various mathematical concepts.
One particularly challenging type of problem you might find on logarithmic equations worksheets involves nested logarithms or logarithms within logarithms, such as logb (logc (x)) = d. These problems require students to carefully apply their knowledge of logarithmic properties and sometimes involve multiple steps to isolate the variable. Solving these equations helps students develop a deeper understanding of how logarithms can be manipulated and how to approach more complex logarithmic functions. This type of problem also introduces students to the concept of composition of functions, which is a critical idea in higher mathematics.
Some logarithmic equations worksheets also include problems that require students to solve for a variable within a logarithmic expression by using inequalities. For example, students might be asked to solve an inequality such as logb (x) > c. These problems are important because they help students understand how the properties of logarithms apply not only to equations but also to inequalities. This practice prepares students for more advanced topics in mathematics, such as calculus, where understanding the behavior of functions is key.
This collection of worksheets features word problems that require the application of logarithmic concepts to real-world scenarios. These problems might involve exponential growth or decay, such as population growth, radioactive decay, or interest calculations, where students must set up and solve a logarithmic equation to find the answer. Word problems like these are particularly valuable because they show students how logarithms are used in practical situations, making the abstract concepts of logarithms more concrete and understandable.
The worksheets also frequently contain problems where students are required to graph logarithmic functions or analyze the behavior of these functions. For instance, students might be asked to sketch the graph of y = logb (x) and analyze its key features, such as intercepts, asymptotes, and end behavior. Graphing problems help students visualize how logarithmic functions behave and how they relate to their corresponding exponential functions. This practice is essential for students who are moving on to more advanced studies in calculus, where understanding the graphical representation of functions is crucial.
Where Do You Find Logarithmic Equations In The Real World?
Logarithmic equations appear in various real-world scenarios, particularly in fields that involve exponential growth, decay, and scaling. Here are some key areas where logarithmic equations are commonly used:
1. Population Growth and Decay – Population Growth – In biology and ecology, logarithmic equations model population growth when resources are limited, leading to a situation where the population grows rapidly at first and then slows down as it approaches a carrying capacity. The logarithmic function helps describe this decelerating growth.
Radioactive Decay – In nuclear physics, the decay of radioactive substances is often modeled using logarithmic equations. The half-life of a substance, which is the time it takes for half of a radioactive sample to decay, is calculated using logarithms.
2. Earthquakes (Richter Scale) – The Richter scale, used to measure the magnitude of earthquakes, is logarithmic. This means that each whole number increase on the scale represents a tenfold increase in amplitude and roughly 31.6 times more energy release. For instance, an earthquake with a magnitude of 7 is ten times more powerful than one with a magnitude of 6 in terms of amplitude.
3. Sound Intensity (Decibels) – The decibel (dB) scale, used to measure sound intensity, is logarithmic. A logarithmic scale is used because the human ear perceives sound intensity logarithmically. For example, an increase of 10 dB represents a tenfold increase in sound intensity, but it is perceived as roughly twice as loud by the human ear.
4. pH Levels in Chemistry – The pH scale, which measures the acidity or basicity of a solution, is logarithmic. pH is defined as the negative logarithm of the hydrogen ion concentration in a solution. This means that each unit change in pH represents a tenfold change in hydrogen ion concentration.
5. Finance (Compound Interest and Growth Rates) – Logarithms are used in finance to model compound interest, where the interest earned is added to the principal, and the interest in subsequent periods is calculated on this new principal. Logarithmic equations help determine the time it will take for an investment to grow to a certain amount or to solve for interest rates over time.
Exponential Growth and Decay – Logarithms are also used in calculating the time required for investments to reach a certain value, or the rate at which a debt grows or decays.
6. Astronomy and Space Science – In astronomy, logarithms are used to measure the brightness of stars (magnitude scale) and the distances between celestial bodies. The apparent magnitude scale, for example, is logarithmic, where a difference of 5 magnitudes corresponds to a 100-fold difference in brightness.
Signal Attenuation – The intensity of signals, such as light or radio waves, decreases logarithmically with distance. This principle is used in calculating the distances of celestial objects based on their observed brightness.