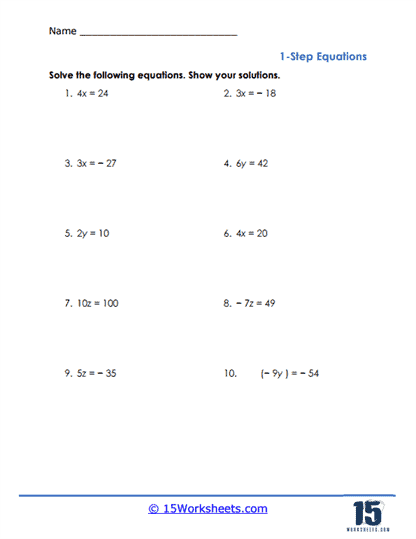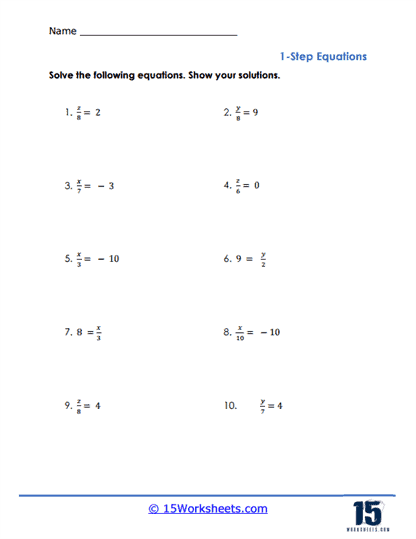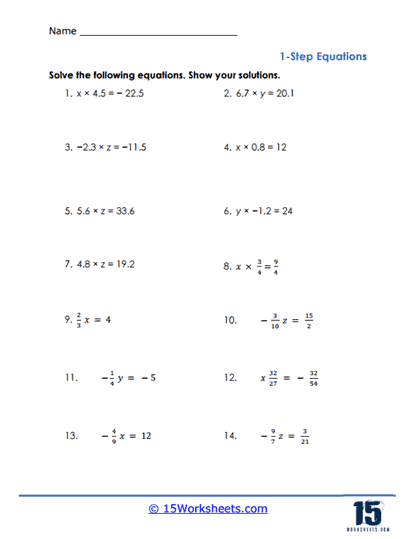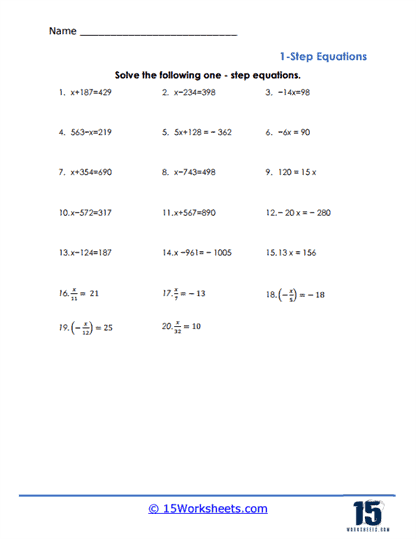One Step Equations Worksheets
About These 15 Worksheets
These worksheets will help students practice and master the fundamental skill of solving algebraic equations that require just one operation to isolate the variable. These worksheets provide a range of problems that target the basic operations-addition, subtraction, multiplication, and division-helping students build confidence in manipulating algebraic expressions and understanding the concept of balance in equations.
The problems presented in these worksheets typically involve equations where the variable is either added to, subtracted from, multiplied by, or divided by a constant number. For instance, students might encounter equations like x + 5 = 12, where they need to subtract 5 from both sides to solve for x, or 3x = 15, where dividing both sides by 3 gives the value of x. Through consistent practice with these types of problems, students reinforce their understanding of how to perform inverse operations to isolate the variable, a crucial skill for more advanced algebraic concepts.
These worksheets may also include problems that require the manipulation of fractions and decimals, adding a layer of complexity that challenges students to apply their knowledge of arithmetic in the context of algebra. For example, students might work with equations like 2/3x = 4, where they need to multiply both sides by the reciprocal of 2/3 to find the value of x. This type of problem helps students understand the importance of precision in algebraic operations and prepares them for more complex equations that involve multiple steps.
The worksheet collection often feature problems that involve negative numbers, both in the constants and in the solutions. These problems teach students how to handle negative values in algebraic contexts, such as in equations like -4x = 20, where dividing by -4 yields x = -5. Understanding how to work with negative numbers is essential for students as they progress in algebra, especially when they begin to solve equations involving inequalities or quadratic expressions.
These types of worksheets not only help students develop procedural fluency but also promote a deeper conceptual understanding of algebra. By consistently solving equations, students internalize the idea that an equation represents a balance, and that whatever operation is performed on one side must also be performed on the other. This foundational concept is vital for success in more advanced topics like systems of equations, inequalities, and functions.
These worksheets often come with a variety of problem formats, ranging from straightforward numeric equations to word problems. Word problems require students to translate a real-world scenario into an algebraic equation before solving it. For example, a problem might describe a situation where a person has a certain amount of money and spends a fixed amount on an item, asking the student to determine how much money remains. This type of problem enhances students’ ability to apply algebraic thinking to practical situations, thereby making the subject more relevant and engaging.
How to Solve a One Step Equation
Example Equation – 3x = 15
Step #1 – Identify the Operation
The equation involves multiplication, where 3 is multiplied by x.
Step #2 – Perform the Inverse Operation
To solve for x, you need to perform the inverse operation of multiplication, which is division.
Divide both sides of the equation by 3 to isolate x.
3x / 3 = 15/3
Step #3 – Simplify
On the left side, the 3s cancel out, leaving you with x.
On the right side, divide 15 by 3, which gives us 5.
The value of x is 5.
Step #4 – Verification
To check if the solution is correct, substitute x = 5 back into the original equation – 3(5) = 15
Since both sides of the equation are equal, the solution x = 5 is correct.