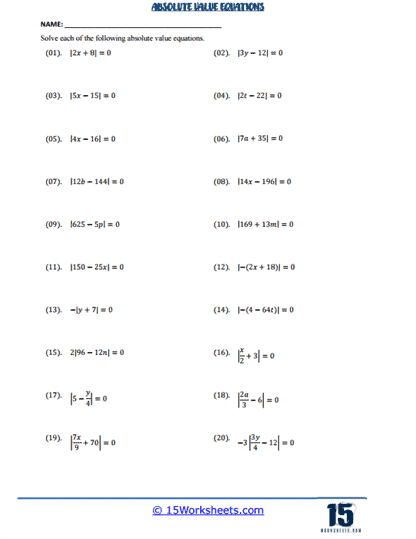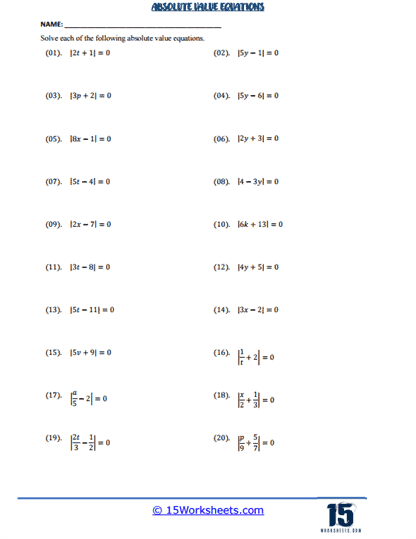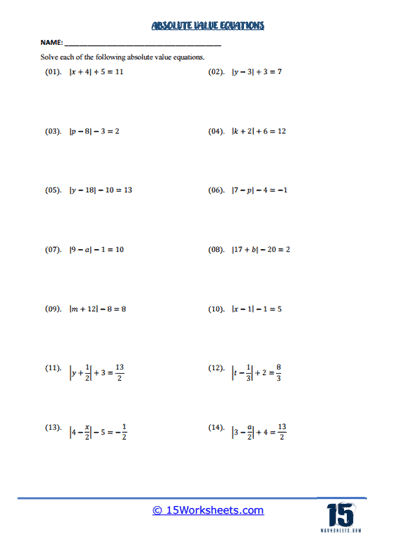Absolute Value Equations Worksheets
About These 15 Worksheets
These worksheets are a vital resource designed to help students grasp the concept of absolute value and how it interacts with algebraic equations. These worksheets typically present a range of problems that require students to solve equations where the variable is within an absolute value expression. The unique challenge of these equations lies in the fact that absolute value represents the distance of a number from zero on the number line, meaning it is always non-negative. Therefore, when solving absolute value equations, students must consider both the positive and negative scenarios that could satisfy the equation.
These worksheets come in various formats, each targeting different aspects of solving absolute value equations. Some worksheets start with more straightforward problems where the absolute value expression is set equal to a number. For instance, a problem might ask students to solve an equation like ∣x + 3∣ = 7. Here, students must recognize that the equation has two potential solutions – x + 3 = 7 and x + 3 = -7, leading to two different values for x. This type of problem introduces students to the fundamental idea that absolute value equations often have two solutions, a concept that is critical for understanding more complex algebraic topics.
As students progress, worksheets may include problems where the absolute value expression is equal to zero or involves more complicated expressions within the absolute value bars. For example, solving ∣2x – 5∣ = 0 teaches students that the only solution occurs when the expression inside the absolute value is zero, reinforcing the idea that absolute value represents distance, which can only be zero if the point is at the origin. This type of problem helps students develop a deeper understanding of how absolute value works and its implications for solving equations.
More advanced worksheets might present absolute value equations where students have to deal with variables on both sides of the equation or equations that involve additional operations outside of the absolute value. For example, solving an equation like ∣3x + 4∣ = 2x + 5 requires students to not only consider the two cases of the absolute value expression but also manage the algebraic manipulation needed to isolate the variable. These problems challenge students to apply their knowledge of both absolute value and algebraic operations, encouraging them to think critically about how to approach and solve more complex equations.
In addition to these basic types of problems, some worksheets introduce inequalities involving absolute values, such as solving ∣x – 3∣ > 5. These problems require students to understand that the inequality represents a range of values for x that satisfy the condition, which can result in two separate inequalities to solve. This type of exercise teaches students how absolute value can create intervals on the number line and how to interpret these intervals within the context of inequality solutions.
The series of practice worksheets also includes a variety of problem types that cater to different learning levels. Beginner worksheets focus on equations where the absolute value expression is set equal to a constant, helping students get comfortable with the basic concept. Intermediate worksheets introduce more complex expressions within the absolute value or include operations outside the absolute value, requiring additional algebraic steps. Advanced worksheets cover absolute value inequalities and equations with variables on both sides, providing challenges that push students to apply their knowledge in new and more demanding ways.
The collection also includes worksheets that address common misconceptions and errors in solving absolute value equations. For example, problems where the absolute value expression is set equal to a negative number, such as ∣x + 2∣ = -3, can be used to reinforce the idea that absolute value cannot be negative, leading to no solution. These types of problems help students understand the boundaries of what absolute value can represent and how it applies in different contexts.
We also have word problems involving absolute value. These problems can help students see the practical applications of absolute value equations in real-world scenarios, such as determining distances, differences, or deviations from a standard value. For example, a word problem might ask students to find the maximum and minimum possible values of a quantity that is allowed to vary by a certain amount, introducing them to the concept of tolerance in manufacturing or quality control.
The collection also includes worksheets that integrate absolute value equations with other algebraic concepts, such as systems of equations, quadratic equations, or even basic functions. For instance, a worksheet might ask students to solve a system of equations where one equation involves an absolute value expression. This type of problem encourages students to think about how different algebraic concepts interact and how absolute value can affect the solution set of an equation.
What Are Absolute Value Equations?
Absolute value equations are mathematical equations that involve the absolute value of a variable expression. The absolute value of a number is its distance from zero on the number line, regardless of direction, which means it is always non-negative. For example, the absolute value of both -5 and 5 is 5. When solving an absolute value equation, such as ∣x – 3∣ = 7, you must consider both the positive and negative solutions that satisfy the equation x – 3 = 7 and x – 3 = -7, leading to the solutions x = 10 and x = -4.
In the real world, the skill of solving absolute value equations is useful in various situations where distance, deviation, or tolerance is involved. For example:
Engineering and Manufacturing – Engineers often work with tolerances, which are acceptable ranges of variation in measurements. For instance, if a machine part is supposed to be exactly 10 mm but can be within 0.1 mm of that measurement, the acceptable measurements can be expressed as ∣x – 10∣ ≤ 0.1, where x represents the actual measurement. Solving this absolute value inequality helps determine the acceptable range of measurements.
Finance – In financial analysis, absolute value equations can be used to calculate deviations in stock prices, interest rates, or other financial metrics from a given benchmark. For example, an investor might want to know how far a stock price can deviate from its average value over a certain period.
Quality Control – In quality control processes, absolute value equations are used to determine how much a product’s characteristics (like weight, size, or concentration) deviate from the desired standard. This ensures products remain within acceptable quality limits.
Navigation and Distance Calculation – Absolute value is used in navigation to determine the distance between two points on a map, regardless of direction. For example, if you’re calculating the distance between two locations along a straight path, the absolute value can help determine how far you need to travel in either direction.
Understanding and solving absolute value equations allows individuals to handle these and other practical situations that require consideration of both positive and negative deviations from a specific value, ensuring accurate and reliable results in real-world applications.