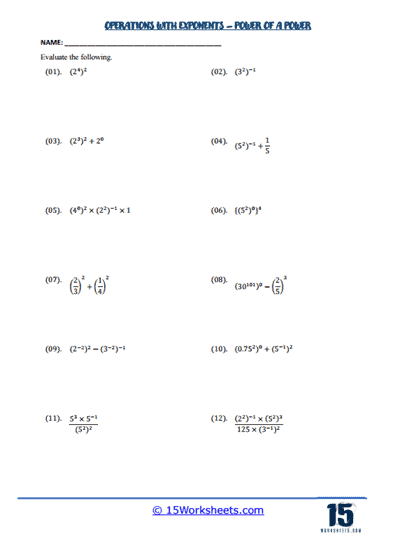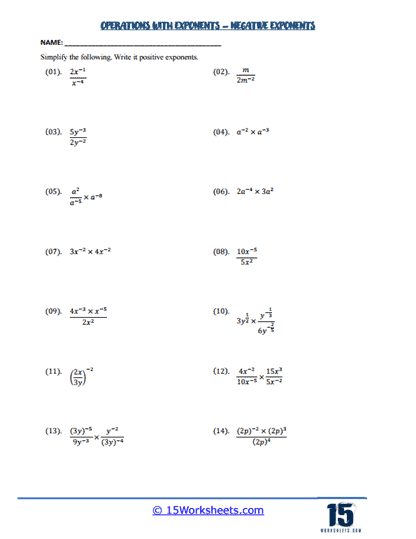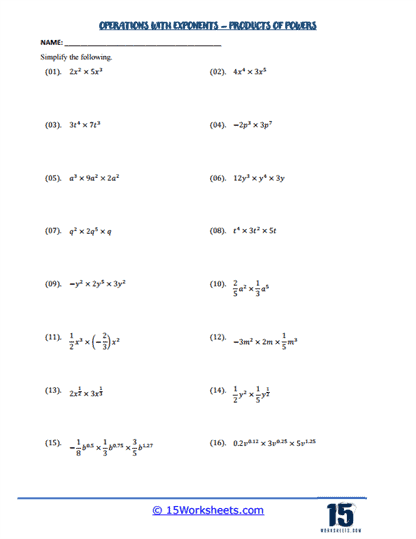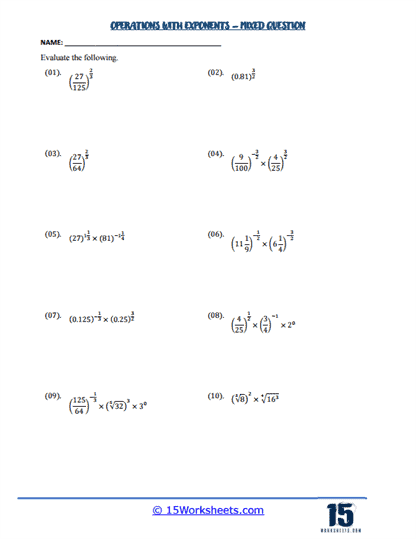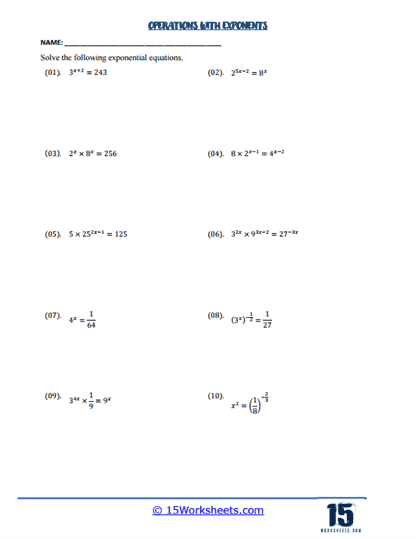Exponential Equations Worksheets

About These 15 Worksheets

These worksheets can help when teaching students how to work with and understand exponents, one of the fundamental concepts in algebra and higher-level mathematics. These worksheets are designed to cover a wide range of skills, from basic exponent notation to more complex operations involving exponents, such as multiplication, division, and applying exponent rules. Each worksheet focuses on different aspects of exponential equations, ensuring that students build a strong, well-rounded foundation in working with exponents.

One of the primary types of worksheets you’ll encounter is the one focused on writing expressions using exponent notation. These worksheets typically present students with repeated multiplication expressions and ask them to rewrite these expressions in exponent form. For example, students might see an expression like x * x * x * x, which they would then convert into x ⁴ . This exercise is crucial for helping students understand the concept of exponents as a shorthand notation for repeated multiplication. It also reinforces the idea that exponents represent the number of times a base is multiplied by itself, a fundamental concept in mathematics.

Another type of worksheet emphasizes the expansion of exponential expressions into their product form. Here, students are given an expression in exponent notation, such as a³b², and asked to expand it, writing it out as a product – a x a x a x b x b. This type of worksheet is vital for reinforcing the understanding that an exponent applies only to the base it is directly attached to, and helps students avoid common mistakes, such as incorrectly applying the exponent to all variables in a term. Additionally, these exercises prepare students for more complex operations by ensuring they can accurately expand and manipulate exponential terms.

Worksheets on the product of powers are another crucial component in learning about exponents. These worksheets typically present students with expressions where two or more exponential terms with the same base are multiplied together. Students must apply the rule that when multiplying like bases, you add the exponents. For example, x³ x x⁴ becomes x^{3 + 4} = x⁷ . This reinforces one of the key exponent rules and helps students develop fluency in manipulating exponential expressions. Understanding this rule is essential for more advanced topics in algebra, such as solving exponential equations and simplifying algebraic expressions.

Division of powers is another important concept covered in Exponential Equations worksheets. These worksheets introduce students to the rule that when dividing like bases, you subtract the exponents. For example, y⁶ ÷ y² simplifies to y^{6 – 2} = y⁴ . This type of exercise helps students understand the inverse relationship between multiplication and division in the context of exponents, which is a foundational concept in algebra. By practicing with these worksheets, students become comfortable with the operations required to simplify expressions involving division of powers, an essential skill for solving more complex algebraic equations.

Negative exponents are often introduced next, typically through worksheets that require students to rewrite expressions with negative exponents as their positive counterparts. For instance, a problem might present x^-3 , which students would rewrite as 1/x³ . This type of worksheet helps students understand that a negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent. Mastering this concept is crucial, as negative exponents frequently appear in various algebraic contexts, including polynomial division and scientific notation.

The power of a power rule is another critical concept that is reinforced through these worksheets. This rule states that when raising a power to another power, you multiply the exponents. For example, (a³)² simplifies to a^{3 x 2} = a⁶ . Worksheets focusing on this rule help students internalize the process of exponent multiplication, which is essential for simplifying more complex expressions and solving higher-level algebraic equations. These worksheets typically present a mix of straightforward applications and more complex scenarios where students must apply multiple rules in sequence, ensuring a deep understanding of the concept.

Substitution in exponent expressions is also a key skill practiced in Exponential Equations worksheets. These worksheets typically present students with an expression involving exponents and require them to substitute specific values for the variables. For example, if given the expression 3x² and the instruction to substitute x = 3, students would calculate 3(3²) = 3(9) = 27. This type of exercise reinforces the practical application of exponent rules and helps students develop the ability to evaluate expressions accurately. It also prepares them for more complex algebraic tasks, such as solving exponential equations and working with functions.

The mixed operations worksheets provide students with a comprehensive review of all the exponent rules they have learned. These worksheets typically include problems that require students to apply multiple exponent rules within a single expression. For example, a problem might involve both the product of powers and the power of a power, requiring students to first add exponents and then multiply them. This type of worksheet is excellent for reinforcing the interconnectedness of the exponent rules and ensuring that students can apply them flexibly in different contexts. It also serves as a diagnostic tool, helping teachers identify which rules students have mastered and which may need further review.

In addition to the basic operations, some worksheets focus on the application of exponents in more complex algebraic expressions. These worksheets might include problems where students must simplify expressions that involve both exponents and other algebraic operations, such as addition, subtraction, or multiplication. For example, a problem might present an expression like 3x² + 2x² , which students must combine by adding the coefficients, resulting in 5x² . These types of problems help students understand how exponent rules interact with other algebraic operations and prepare them for solving more complex equations.

Our more advanced worksheets introduce students to fractional exponents, which represent roots. For instance, x^1/2 is equivalent to the square root of x. These worksheets challenge students to convert between radical and exponential forms, as well as to simplify expressions involving fractional exponents. Understanding fractional exponents is crucial for higher-level math, as they frequently appear in calculus and advanced algebra. These worksheets help bridge the gap between basic exponent rules and more advanced mathematical concepts, ensuring that students have a well-rounded understanding of exponents.