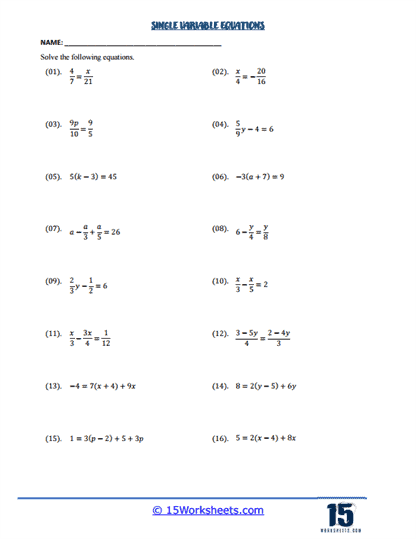Algebra Worksheets
Related Worksheets
About These 15 Worksheets
These worksheets will help students practice, reinforce, and master various algebraic concepts and skills. These worksheets typically cover a wide range of topics, from basic equation solving to more complex applications involving multiple steps and different mathematical principles. They are organized to challenge students at different levels of proficiency, ensuring a gradual and thorough understanding of algebraic operations and their applications.
One common type of algebra worksheet focuses on solving one-step equations. These exercises are fundamental in algebra, as they help students understand the basic operations of addition, subtraction, multiplication, and division in the context of algebra. For example, students might be asked to solve simple equations like x + 5 = 12 or 3x = 15. The goal is to isolate the variable on one side of the equation, which reinforces the concept of balancing equations-a core idea in algebra. These worksheets typically provide practice in manipulating equations involving integers, fractions, and decimals, helping students gain confidence in their ability to solve equations quickly and accurately.
Another important category includes two-step equations and word problems. Two-step equations require students to perform two operations to solve for the variable, such as solving equations like 2x + 3 = 11. These worksheets help students understand the sequence of operations and the logic behind solving more complex equations. Word problems add an additional layer of complexity by requiring students to translate a written scenario into an algebraic equation before solving it. This not only tests their algebra skills but also their ability to interpret and model real-world situations mathematically. For instance, a problem might describe a situation where a certain number of items are purchased at different prices, and students must figure out the total cost or remaining budget.
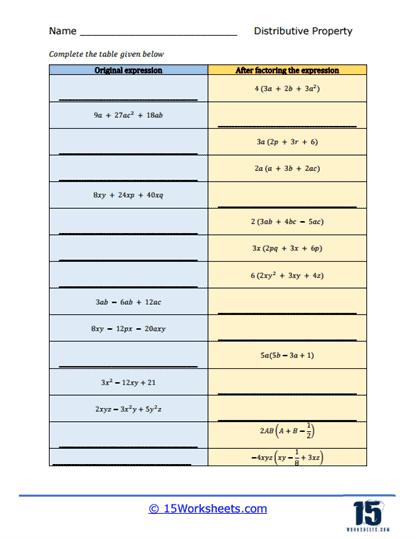
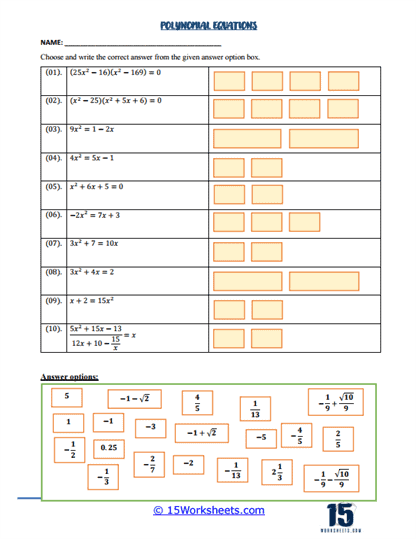
Moving on to more advanced topics, some worksheets focus on four-step equations. These problems are designed to challenge students with equations that require multiple steps and operations, such as combining like terms, distributing, and then solving the resulting simpler equation. These types of problems help students develop critical thinking and problem-solving skills, as they must carefully consider the order of operations and the logical steps needed to isolate the variable. For example, a problem might involve an equation like 3(2x – 5) + 4 = 2x + 10, where students need to distribute, combine like terms, and then solve for x.
Worksheets on absolute value equations are another key component of algebra practice. These problems require students to understand that absolute value represents the distance from zero, regardless of direction, and therefore can result in two possible solutions for an equation. For instance, solving ∣x – 3∣ = 5 means considering both x- 3 = 5 and x – 3 = -5. These exercises help students grasp the concept of absolute value and apply it in solving equations, reinforcing their understanding of how different mathematical operations affect the solution set of an equation.
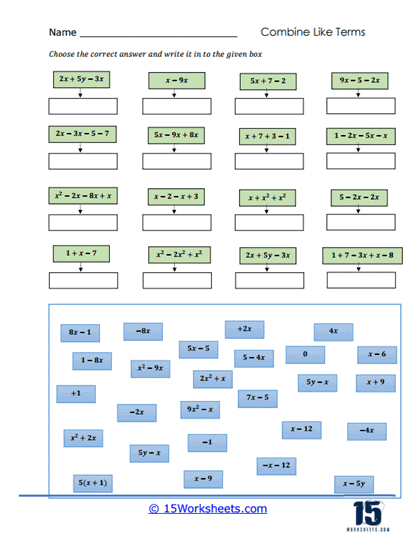
In algebra, the ability to combine like terms is crucial for simplifying expressions and solving equations. Worksheets focused on this skill typically present a variety of expressions that students must simplify by combining terms with the same variable part. For example, an expression like 2x + 3x – 5 can be simplified to 5x – 5. These exercises teach students how to identify like terms, add or subtract coefficients, and simplify expressions, which are necessary skills for more advanced algebraic manipulations.
Equations involving percentages are also common in algebra worksheets, especially as students begin to explore applications of algebra in real-world contexts. These problems often involve finding a percentage of a number, increasing or decreasing a number by a percentage, or solving for a value given its percentage relation to another value. For instance, a problem might ask students to find the percentage of students who passed an exam out of the total number of students, or to calculate the original price of an item after a discount has been applied. These exercises are particularly useful for teaching students how to apply algebraic thinking to everyday financial situations, such as shopping, budgeting, and understanding interest rates.
Logarithmic equations represent a more advanced topic in algebra, where students must apply the rules of logarithms to solve equations. These worksheets typically require students to use properties such as the product, quotient, and power rules to simplify and solve logarithmic expressions. For example, solving an equation like log(x) + log(2) = log(6) might involve applying the product rule to combine logarithms before solving for x. These exercises help students develop a deeper understanding of logarithms, which are essential for more advanced studies in mathematics and science.
Worksheets on operations with exponents and zero exponents are crucial for building a solid foundation in algebra. These exercises teach students the rules for multiplying, dividing, and raising powers to powers, as well as understanding the significance of a zero exponent. For instance, students might solve problems like (2x3) (3x2) or simplify expressions like x0 . These skills are fundamental not only in algebra but also in higher-level math courses, such as calculus and physics, where exponential functions and operations frequently appear.
What Is Algebra?
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols to solve equations and understand relationships between quantities. These symbols, often represented by letters such as x, y, and z, stand for numbers, and the process of algebra involves finding the values of these variables that make certain equations true. Unlike arithmetic, which deals with specific numbers and straightforward calculations, algebra introduces the concept of generalization, allowing for the expression of complex relationships in a more abstract form. This abstraction enables algebra to solve problems that are not confined to specific numerical cases, making it a powerful tool in mathematics.
Algebra is used in a wide array of fields and everyday situations. In science and engineering, algebra is essential for modeling and solving problems that involve relationships between varying quantities, such as the motion of objects, electrical circuits, or chemical reactions. In economics, algebra helps in understanding and predicting changes in markets, calculating interest rates, and optimizing business operations. In computer science, algebraic principles underpin algorithms, data structures, and cryptography. Even in daily life, algebra is often used, whether in calculating a budget, adjusting a recipe, or determining the amount of paint needed for a room. Algebra’s ability to generalize and simplify problems makes it an indispensable tool for problem-solving in both academic and practical contexts.