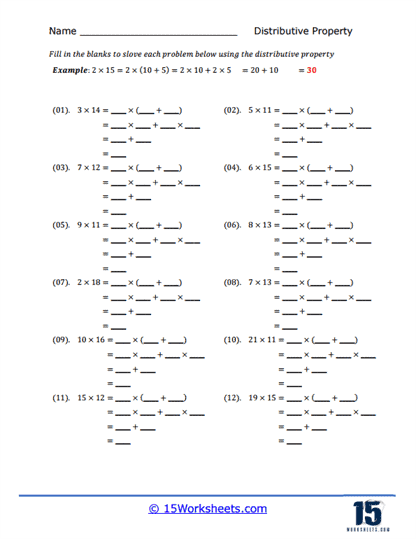Distributive Property Worksheets
About These 15 Worksheets
These worksheets provide students with a systematic approach to understanding and applying the distributive property. This algebraic property is a cornerstone of arithmetic and algebra, allowing students to simplify expressions and solve equations more efficiently. These worksheets are designed to help students grasp the concept of distributing multiplication over addition or subtraction within an expression, and they offer various exercises that reinforce this skill through practice and repetition.
One type of worksheet focuses on matching expressions with their simplified forms. This exercise helps students recognize how the distributive property works by allowing them to see the process of distribution in action. For example, a student might be given an expression like 2(p + 7) – 3p and asked to match it with the corresponding simplified form in another column. This type of exercise emphasizes the importance of performing operations inside the parentheses first, followed by distributing the multiplication to each term within the parentheses. Students learn how to identify and pair equivalent expressions, which reinforces their understanding of how the distributive property simplifies and reorganizes algebraic expressions.
Another common worksheet type involves solving equations using the distributive property. In these exercises, students are tasked with applying the distributive property to break down expressions before solving for the unknown variable. For instance, a problem might present an equation like 3(p – 2) = 9, requiring students to first distribute the 3 across the p – 2 and then solve the resulting equation. This approach helps students understand how the distributive property is used in more complex algebraic operations, especially when dealing with linear equations. By practicing these types of problems, students become more adept at recognizing when and how to apply the distributive property to simplify and solve equations efficiently.
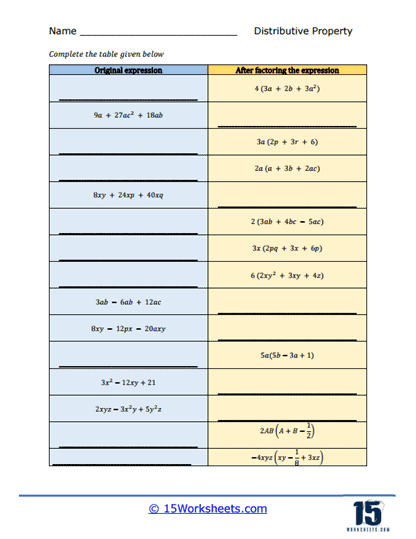
Worksheets that require students to factor expressions using the distributive property provide another layer of complexity. In these exercises, students are given a simplified expression and must work backward to factor out the greatest common factor, effectively reversing the distributive process. For example, given an expression like 8x + 24y, students must recognize that both terms share a common factor of 8, allowing them to rewrite the expression as 8(x + 3y). This type of problem reinforces students’ understanding of the distributive property by showing them how to identify common factors and factor them out, a crucial skill in simplifying algebraic expressions and solving more advanced equations.
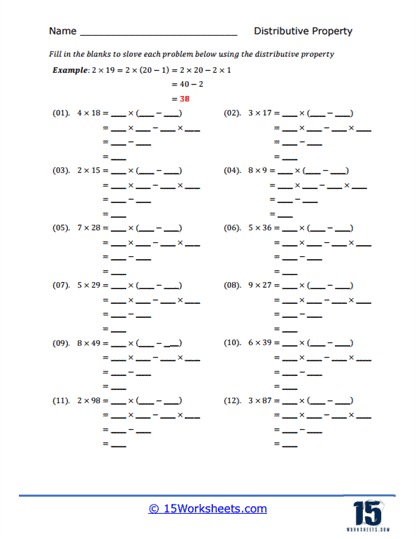
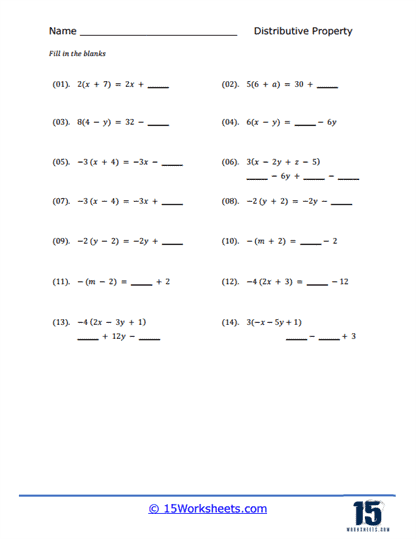
Some worksheets focus on the direct application of the distributive property to solve problems, often presented in a fill-in-the-blank format. These exercises typically present an expression or equation with missing components, challenging students to correctly distribute and complete the equation. For example, a problem might present 5(x + 3) and ask students to fill in the missing terms after distribution, resulting in 5x + 15. This type of worksheet not only reinforces the mechanical aspect of the distributive property but also encourages students to think critically about each step of the process, ensuring they understand both the concept and its application.
Simplification exercises are another key component of distributive property worksheets. In these problems, students are given complex expressions that require multiple applications of the distributive property to simplify fully. For instance, an expression like 3(2x + 4) – 5(x – 2) challenges students to distribute both the 3 and the -5 before combining like terms to reach a simplified form. These problems help students develop a deeper understanding of how the distributive property interacts with other algebraic principles, such as combining like terms and simplifying complex expressions.
Some of the worksheets may focus on writing algebraic expressions as products of their factors using the distributive property. This exercise is particularly useful in helping students see the connection between multiplication and factoring, two fundamental concepts in algebra. For example, students might be asked to express ab + ac as a(b + c), highlighting how the distributive property can be used to factor expressions and solve equations more efficiently. This type of problem is crucial for developing a strong foundation in algebra, as it bridges the gap between multiplication and division, helping students understand the dual nature of these operations.
The worksheets might include word problems that require the application of the distributive property to solve real-world scenarios. These problems help students see the relevance of the distributive property beyond the classroom, demonstrating how it can be used to simplify and solve problems in everyday life. For example, a word problem might describe a situation where a person needs to distribute resources equally among several groups, and the student must use the distributive property to determine the total amount required. These exercises not only reinforce students’ understanding of the property but also help them develop critical thinking skills by applying mathematical concepts to real-world situations.
Through consistent practice with these various types of distributive property worksheets, students gain a comprehensive understanding of how to apply this crucial algebraic principle in different contexts. They learn to recognize when and how to use the distributive property to simplify expressions, solve equations, factor algebraic expressions, and solve real-world problems. As they progress, students become more confident in their ability to tackle increasingly complex algebraic problems, building a solid foundation for future math courses and standardized tests.
What is the Distributive Property?
The Distributive Property is a fundamental principle in algebra that allows you to multiply a single term across the terms within a parenthesis. It is one of the key properties that help in simplifying algebraic expressions and solving equations. This property shows that multiplying a number by a group of numbers added together is the same as doing each multiplication separately.
Mathematically, the Distributive Property is expressed as – a(b + c) = ab + ac
Here, a, b, and c can be any real numbers, variables, or algebraic expressions. According to the Distributive Property, if you have a number or variable outside the parentheses, you distribute it to each term inside the parentheses, multiplying it by each term separately. The results are then summed to give the final expression.
This property is essential because it simplifies complex expressions, making them easier to work with. It also plays a crucial role in solving equations, especially when dealing with linear equations, polynomials, and factoring expressions. The Distributive Property is not just limited to addition inside the parentheses; it also applies to subtraction, which can be thought of as adding a negative.
The distributive property works both ways – you can distribute a factor over terms inside parentheses, or you can factor a common factor out of terms, which is essentially reversing the distribution process. This flexibility makes it an incredibly powerful tool in algebraic manipulations.
Simplifying an Algebraic Expression
Let’s consider a situation where we need to simplify the expression – 3(x + 4)
According to the Distributive Property, we need to multiply 3 by each term inside the parentheses – 3(x + 4) = 3⋅x + 3⋅4
Simplifying the multiplication gives us – 3x + 12
Solving an Equation
Consider the equation – 5(2y – 3) = 20
To solve for y, we first apply the Distributive Property to remove the parentheses – 5(2y – 3) = 5⋅2y – 5⋅3
This simplifies to – 10y – 15 = 20
Next, to isolate y, we first add 15 to both sides of the equation – 10y – 15 + 15 = 20 + 15
Simplifying gives – 10y = 35
Finally, divide both sides by 10 – y = 35/10 = 3.5
In this example, the Distributive Property was crucial in simplifying the equation and making it easier to solve.