Polynomial Equations Worksheets
About These 15 Worksheets
These worksheets are great for helping students master the skills needed to solve polynomial equations, which are algebraic expressions involving terms that include variables raised to whole-number exponents. These worksheets cover a wide range of problems, from simple factorable equations to more complex polynomials, offering students a thorough understanding of how to handle equations of varying degrees and forms. By systematically working through these types of problems, students develop the critical thinking and problem-solving skills necessary for higher-level algebra and calculus.
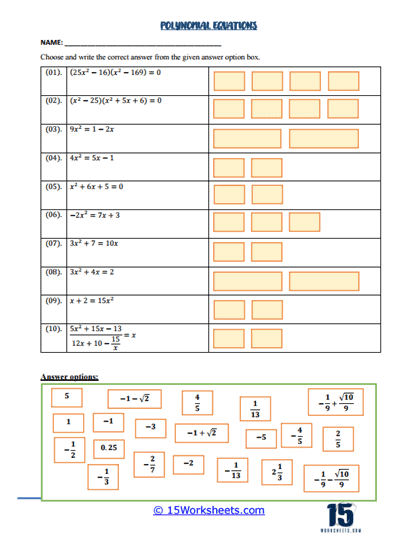
One of the fundamental types of problems found in Polynomial Equations worksheets involves solving quadratic equations that are already factored. These worksheets present equations in the form (x – a)(x – b) = 0, where students must apply the zero-product property. This property states that if a product of factors equals zero, at least one of the factors must be zero. Thus, students learn to set each factor equal to zero and solve for the variable, which reinforces their understanding of how polynomials can be broken down into simpler linear factors. This foundational skill is essential not only for solving basic quadratic equations but also for understanding more complex polynomials that can be factored into multiple linear terms.
Another critical type of problem presented in these worksheets involves solving quadratic equations that require additional algebraic manipulation before they can be solved. For example, students might encounter equations that require them to first move all terms to one side of the equation or to apply the distributive property before factoring. This type of exercise teaches students the importance of simplifying equations as much as possible before attempting to solve them. It also helps them develop a step-by-step approach to solving polynomial equations, which is crucial for more complex problems where multiple steps are required to isolate the variable.
In addition to these simpler equations, these worksheets often include problems that involve higher-degree polynomials, such as cubic or quartic equations. These problems introduce students to the challenge of dealing with equations that have more than two roots. Students must learn to apply their factoring skills to these more complex polynomials, often using synthetic division or the Rational Root Theorem to find potential roots before fully factoring the equation. Working with higher-degree polynomials helps students understand the relationship between the degree of the polynomial and the number of solutions the equation can have, which is an important concept in algebra and calculus.
Another significant feature of our polynomial equations worksheets is the inclusion of problems that require students to solve polynomial equations by using the quadratic formula. This formula, which is used to find the roots of a quadratic equation, is an essential tool for any algebra student. Worksheets often present equations that are not easily factorable, requiring students to apply the quadratic formula to find the solutions. By practicing with the quadratic formula, students learn how to handle equations that do not factor neatly and develop confidence in their ability to solve a wide variety of quadratic equations.
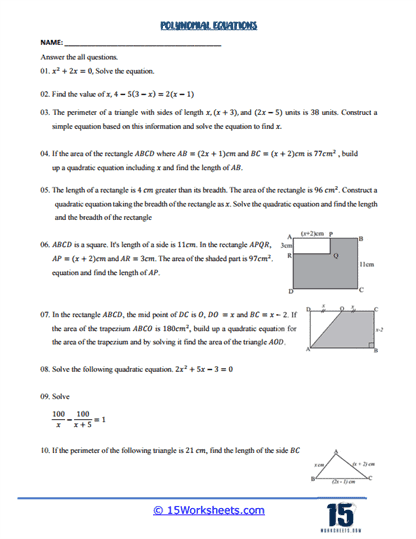
Beyond these algebraic techniques, some of the worksheets also include word problems that require students to translate real-world scenarios into polynomial equations. These problems are particularly valuable because they teach students how to apply their mathematical skills in practical situations. For example, students might be asked to model the trajectory of a projectile or the growth of a population using a polynomial equation. These word problems not only reinforce students’ understanding of polynomial equations but also help them see the relevance of algebra in everyday life.
Some of the worksheets include problems that involve systems of polynomial equations, where students must solve for multiple variables simultaneously. These systems can be solved using substitution, elimination, or graphing methods. Working with systems of equations helps students develop a deeper understanding of how different polynomial equations can interact with one another and how solutions can be found that satisfy all equations in the system. This type of problem-solving is crucial for students who plan to pursue advanced studies in mathematics, engineering, or the sciences, where systems of equations are frequently used to model complex phenomena.
Another advanced topic covered in this worksheet series is the use of polynomial identities and theorems, such as the Binomial Theorem or the Remainder Theorem. These concepts are essential for understanding how polynomials behave under certain operations and for solving more complex equations that cannot be easily factored or simplified. For example, the Remainder Theorem can be used to find the remainder when a polynomial is divided by a linear divisor, which is helpful in solving polynomial equations that involve division. By working through problems that involve these theorems, students gain a deeper understanding of the properties of polynomials and how they can be manipulated to solve equations.
Some worksheets also include matching or multiple-choice problems where students must select the correct solution from a set of options. These types of problems are useful for reinforcing students’ understanding of polynomial equations in a slightly different format. Instead of working through the entire solution, students must recognize patterns and apply their knowledge quickly to identify the correct answer. This helps to solidify their understanding of the key concepts and provides a different type of challenge compared to more traditional problem-solving exercises.
Another important skill taught by these types of worksheets is the ability to check solutions for accuracy. This is particularly important when dealing with more complex polynomials that have multiple steps in their solutions. Worksheets often encourage students to substitute their solutions back into the original equation to verify that they are correct. This practice not only reinforces the accuracy of their work but also helps students develop the habit of double-checking their answers, which is a valuable skill in all areas of mathematics.