Trigonometric Identities Worksheets
About These 15 Worksheets
These worksheets are a key resource for students learning the intricate relationships between different trigonometric functions. These worksheets are designed to strengthen students’ understanding of fundamental concepts in trigonometry by providing a variety of exercises that challenge them to apply, simplify, and prove these identities. The goal is not just to memorize the identities but to understand how they work and how they can be used to simplify complex trigonometric expressions, solve equations, and prove mathematical statements.
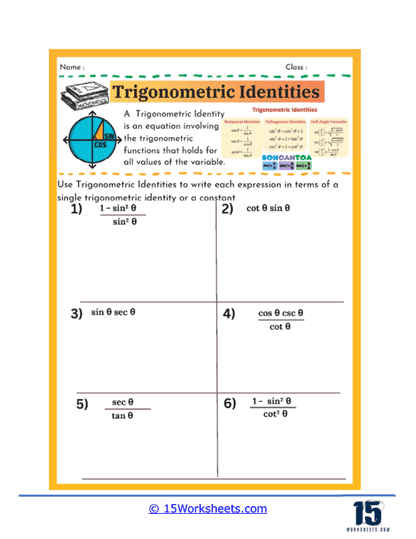
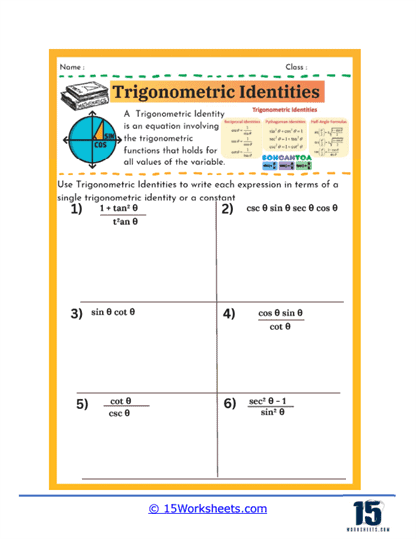
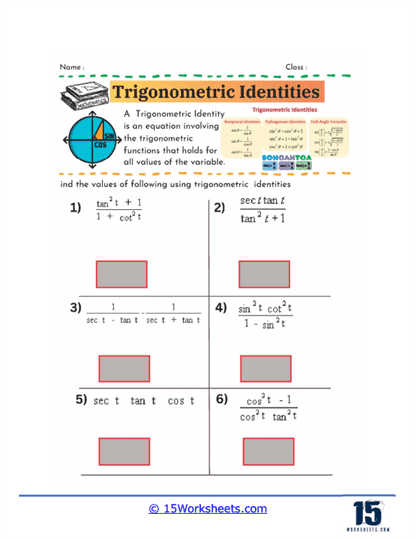
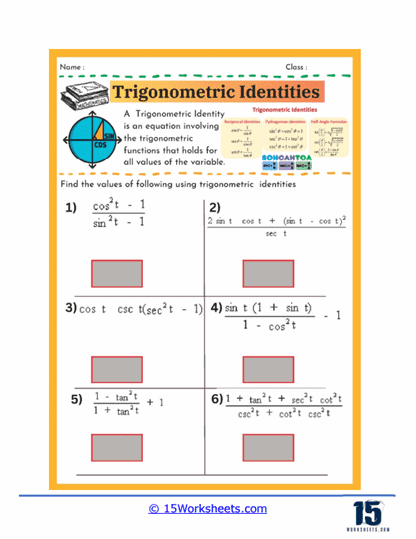
One of the primary focuses of these worksheets is on simplifying trigonometric expressions using identities. Students encounter problems where they are given complex trigonometric expressions and are required to reduce them to their simplest form. This process typically involves using basic identities such as the Pythagorean identities, reciprocal identities, or quotient identities. For instance, students might be asked to simplify an expression involving sine and cosine into a single trigonometric function or a constant. This kind of exercise helps students recognize patterns and develop a deeper understanding of how different trigonometric functions relate to one another. It also sharpens their algebraic manipulation skills as they combine like terms, factor expressions, or rationalize denominators to achieve the simplest form.
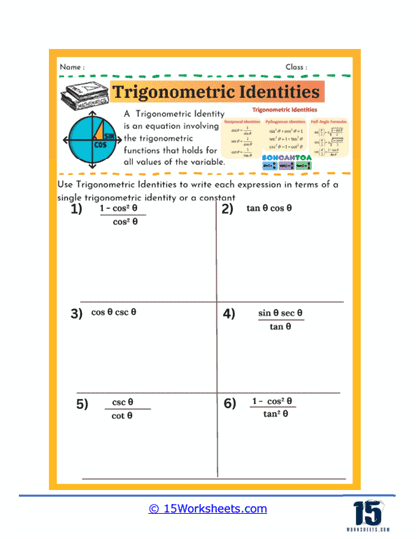
Another type of exercise commonly found on trigonometric identities worksheets involves rewriting expressions in terms of a single trigonometric function. For example, students might be given an expression that includes multiple trigonometric functions and be tasked with expressing the entire equation in terms of sine, cosine, or another single function. This practice is crucial because it allows students to see how different trigonometric functions can be interconverted, making complex problems easier to solve. It also lays the groundwork for solving more advanced equations where expressing everything in terms of one function is often a key step.
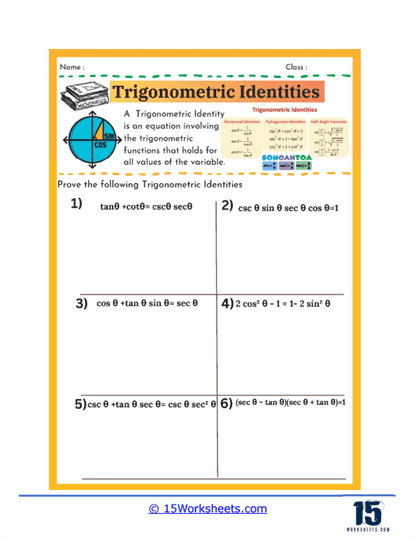
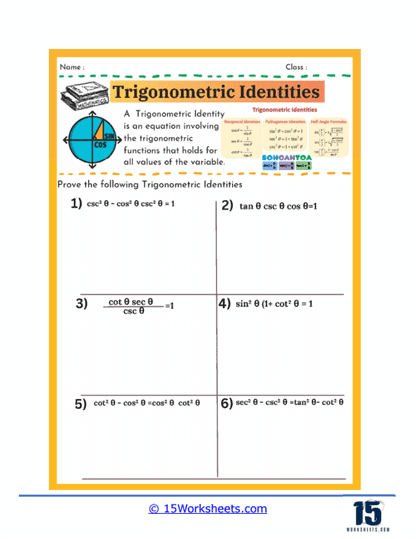
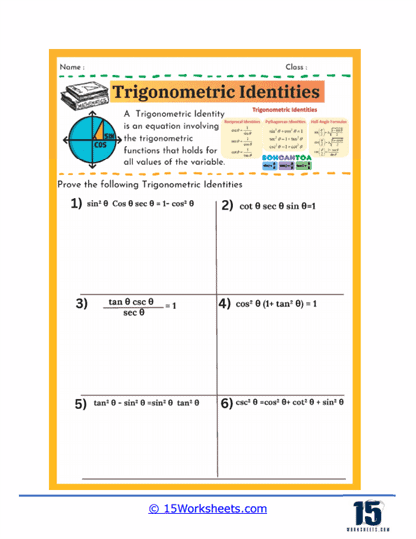
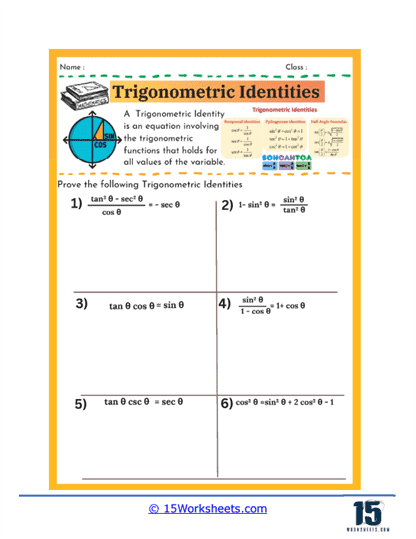
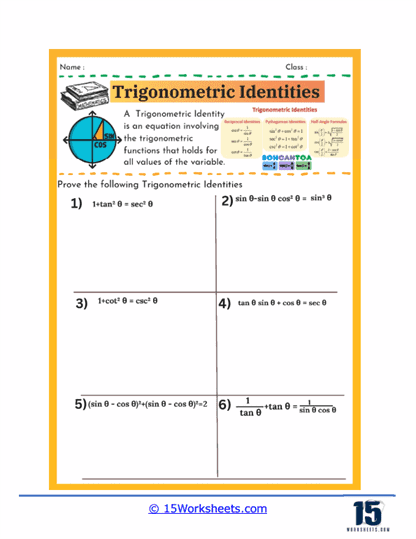
Proving trigonometric identities is another critical component of these worksheets. In this type of exercise, students are given an equation that purports to be an identity-that is, a statement that is true for all values within a certain range-and must prove that it holds true. This process involves a combination of algebraic manipulation and the application of known identities. For example, students might start with one side of the equation and work step by step to transform it into the other side, thereby proving the identity. These exercises are particularly valuable because they teach students not only to recognize valid identities but also to construct logical, step-by-step arguments-skills that are vital in all areas of mathematics.
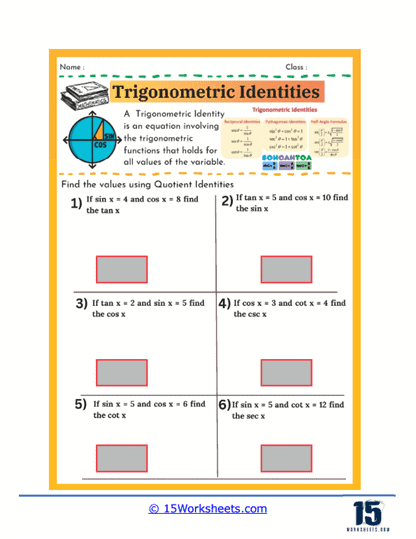
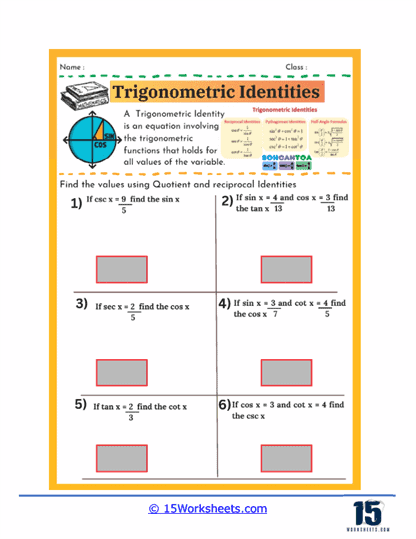
Some worksheets also focus on finding the values of trigonometric functions using quotient identities. In these exercises, students might be given values for one trigonometric function and asked to find another using the relationship between them. For example, if students know the value of sine and cosine, they can use the quotient identity to find the value of tangent. These problems are excellent for reinforcing the connections between different trigonometric functions and for helping students practice using identities in practical, problem-solving contexts.
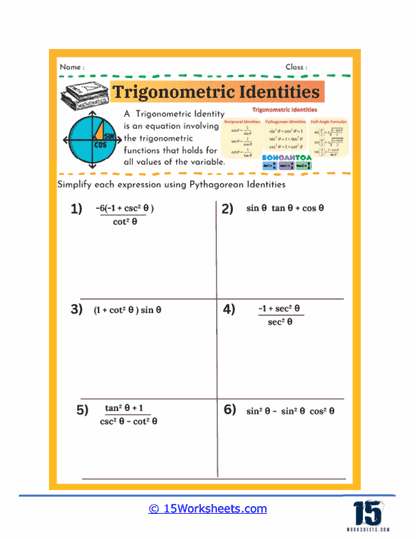
Another important skill that these worksheets develop is the ability to simplify expressions using Pythagorean identities. Students might be given an expression involving squares of sine and cosine, for example, and asked to simplify it using the identity that relates these two functions. These exercises are particularly useful for helping students understand how the Pythagorean theorem underpins many of the relationships in trigonometry, as well as for giving them practice in algebraic manipulation.
In addition to simplification and proof exercises, some worksheets also challenge students to find the values of trigonometric functions using more complex identities or combinations of identities. For example, students might be asked to find the value of a trigonometric function given a specific angle or to work with expressions that involve multiple steps and multiple identities. These problems are designed to push students’ understanding of trigonometric identities to a deeper level and to prepare them for the kinds of complex problems they will encounter in higher-level mathematics courses.
Throughout all these exercises, the emphasis is on developing a deep understanding of how trigonometric identities work and how they can be applied in a variety of contexts. Students learn to see the connections between different identities, to recognize when and how to use specific identities, and to develop the algebraic skills needed to manipulate and simplify complex expressions. This process not only strengthens their understanding of trigonometry but also builds their overall problem-solving skills, logical reasoning abilities, and mathematical fluency.
They provide students with the practice they need to master these identities and to apply them in solving equations, proving identities, and simplifying expressions. By working through these worksheets, students gain confidence in their ability to handle complex trigonometric problems and prepare themselves for more advanced studies in mathematics. Whether they are simplifying expressions, proving identities, or finding the values of trigonometric functions, students who work with these worksheets develop a strong foundation in trigonometry that will serve them well in any mathematical or scientific field.
What Are Trigonometric Identities?
Trigonometric identities are mathematical expressions that show the relationships between different trigonometric functions, such as sine, cosine, and tangent. These identities are considered “true” for all values of the variables involved within their domains, meaning they hold under any circumstance within their defined range. Essentially, trigonometric identities are like the “rules” of trigonometry that allow mathematicians and students to simplify and solve complex problems. They help to connect various trigonometric functions together in ways that might not be immediately obvious, making it possible to transform and manipulate expressions in useful ways.
One of the most important aspects of trigonometric identities is their role in simplifying complex trigonometric expressions. In mathematics, and especially in trigonometry, it’s common to encounter long and complicated expressions involving multiple trigonometric functions. Without trigonometric identities, simplifying these expressions would be extremely challenging, if not impossible. By applying the appropriate identities, one can reduce a complicated expression to a much simpler form, which makes it easier to understand and work with. This simplification process is crucial not only in pure mathematics but also in applied fields like engineering and physics, where managing complex equations is a routine part of problem-solving.
In the real world, trigonometric identities are particularly helpful in any situation that involves waves, circles, or oscillatory motion. For example, in physics, trigonometric identities are used to analyze sound waves, light waves, and other types of waves. Engineers often use these identities to design and analyze systems that involve periodic motion, such as vibrating strings, pendulums, or electrical circuits that have alternating currents. In these cases, trigonometric identities allow engineers and scientists to model and predict the behavior of these systems accurately. For instance, they can help in determining the amplitude, frequency, and phase of waves, which are critical parameters in fields like acoustics, optics, and electronics.
Another practical application of trigonometric identities is in the field of signal processing, which involves the analysis and manipulation of signals-like sound, radio waves, or images. In signal processing, trigonometric identities are used to transform signals from one form to another, making it easier to filter out noise, compress data, or extract important information. This is particularly important in telecommunications, where signals need to be transmitted over long distances without losing quality. By applying trigonometric identities, engineers can design systems that efficiently transmit and receive signals, ensuring clear communication across the globe.
In architecture and construction, trigonometric identities play a crucial role in design and structural analysis. Architects and engineers use trigonometry to calculate angles and distances, ensuring that buildings are both aesthetically pleasing and structurally sound. For example, when designing roofs, ramps, or any other part of a building that involves sloping surfaces, trigonometric identities help determine the correct angles and lengths. This ensures that the structures can withstand various forces and loads, such as wind, gravity, and earthquakes. Moreover, trigonometric identities are also used in computer graphics and animation, where they help in rendering images, simulating motion, and creating realistic visual effects.
In navigation and geography, trigonometric identities are essential for determining locations and plotting courses. Navigators use these identities to calculate distances and angles between different points on the Earth’s surface. This is particularly important in aviation and maritime navigation, where precise calculations are necessary to ensure safe and efficient travel. Trigonometric identities also play a key role in satellite navigation systems like GPS, which rely on the accurate calculation of distances and angles to pinpoint locations anywhere on the planet. Without these identities, the technology that enables modern navigation and global communication would not be possible.
Trigonometric identities are also used in astronomy to study the positions and movements of celestial bodies. Astronomers apply these identities to calculate the angles and distances between stars, planets, and other objects in space. This allows them to map the night sky, predict the movements of planets, and understand the dynamics of galaxies. In astrophysics, trigonometric identities help scientists model the behavior of complex systems, such as binary star systems or the orbits of satellites around planets. These applications are crucial for advancing our understanding of the universe and for developing technologies that rely on space-based observations, such as weather forecasting and satellite communication.