Trigonometry Worksheets
About These 15 Worksheets
These worksheets can help students understand and apply the principles of trigonometry through structured practice. These worksheets cover a wide range of topics, catering to different skill levels and learning objectives. By engaging with various types of trigonometry worksheets, students can develop a strong foundation in understanding angles, triangles, and the relationships between their sides and angles. Let’s explore the different types of trigonometry worksheets and the math skills they help to build.
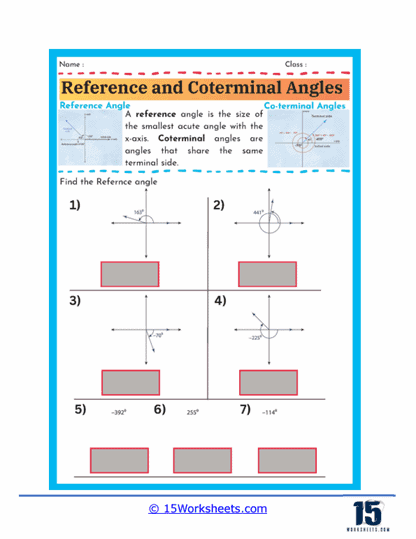
1. Introduction to Trigonometric Ratios
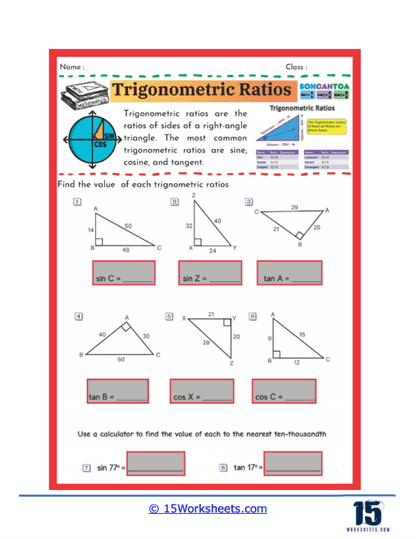
One of the fundamental types of trigonometry worksheets focuses on introducing students to the basic trigonometric ratios: sine, cosine, and tangent. These worksheets typically present right-angled triangles where students are required to identify and calculate these ratios based on given side lengths. Problems may involve finding the ratio values when two sides are known or determining missing side lengths using known angles and sides.
Through these exercises, students learn how to relate the angles of a triangle to its sides, which is essential for solving more complex problems later on. They also become comfortable with using the definitions of sine, cosine, and tangent in various contexts. Mastering these basic ratios sets the stage for understanding more advanced trigonometric concepts and applications.
2. Solving Right Triangles
Another common type of worksheet involves solving right triangles by applying trigonometric ratios. In these worksheets, students are presented with right-angled triangles where some sides and angles are known, and they must use trigonometric functions to find the missing measurements. Problems may require students to calculate unknown side lengths when an angle and a side are given or determine angle measures when two sides are known.
Working through these problems helps students develop problem-solving skills and reinforces their understanding of how trigonometric ratios can be applied to real-world situations. These worksheets often include word problems that depict practical scenarios, such as determining the height of a building or the distance across a river, thereby illustrating the usefulness of trigonometry in everyday life.
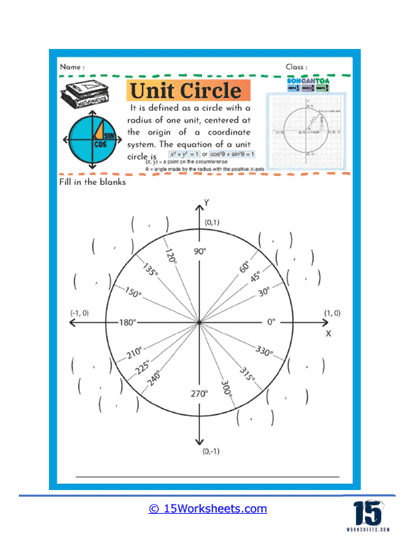
3. Understanding the Unit Circle
Worksheets centered around the unit circle are essential for deepening students’ comprehension of trigonometric functions beyond right-angled triangles. These worksheets typically involve exercises where students identify and compute the values of sine, cosine, and tangent for various angles measured in degrees and radians around the unit circle. Activities may include filling out unit circle diagrams, converting between degrees and radians, and evaluating trigonometric functions at standard angles.
By working with the unit circle, students learn how trigonometric functions behave over different angles and how they repeat in a periodic manner. This understanding is crucial for advanced studies in trigonometry, including graphing trigonometric functions and solving trigonometric equations. Additionally, familiarity with the unit circle aids in recognizing patterns and symmetries within trigonometric functions.
4. Graphing Trigonometric Functions
Graphing trigonometric functions is another important topic covered by specialized worksheets. These worksheets provide exercises where students plot sine, cosine, and tangent functions over specified intervals. Problems may involve identifying key characteristics such as amplitude, period, phase shift, and vertical shift, and then using this information to sketch accurate graphs.
Engaging with these worksheets enables students to visualize how trigonometric functions behave and change under different transformations. They learn how altering parameters affects the shape and position of the graphs, which is vital for understanding oscillatory phenomena in physics and engineering. Additionally, students develop skills in interpreting and analyzing graphical data, which is applicable across various scientific disciplines.
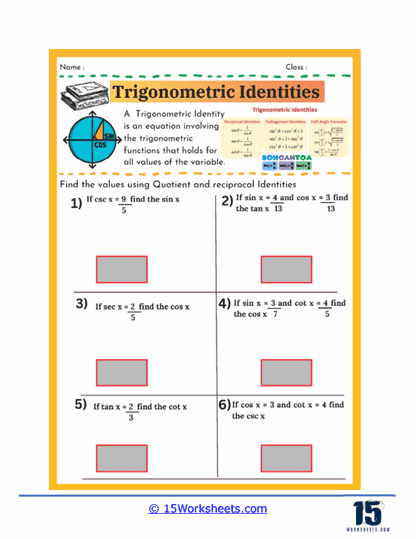
5. Trigonometric Identities and Simplification
Worksheets focusing on trigonometric identities help students learn how to simplify complex trigonometric expressions and prove fundamental relationships between trigonometric functions. These exercises often involve applying identities such as the Pythagorean, angle sum and difference, double angle, and half-angle identities. Problems may range from straightforward simplifications to more challenging proofs that require combining multiple identities.
Through consistent practice with these worksheets, students enhance their algebraic manipulation skills and deepen their understanding of the interconnectedness of trigonometric functions. Mastery of trigonometric identities is essential for solving complex trigonometric equations and plays a significant role in calculus and higher-level mathematics. It also fosters logical reasoning and proof-writing abilities.
6. Solving Trigonometric Equations
Another category of trigonometry worksheets involves solving trigonometric equations for unknown angles or values within specified intervals. These problems require students to apply their knowledge of trigonometric identities and inverse functions to find all possible solutions that satisfy the given equations. Exercises may vary from simple equations involving a single trigonometric function to more complex ones that require factoring and the use of multiple identities.
Working through these worksheets helps students develop critical thinking and problem-solving strategies. They learn to approach equations systematically, consider multiple solution paths, and verify the validity of their answers within given contexts. These skills are particularly useful in advanced mathematics and physics, where trigonometric equations frequently arise.
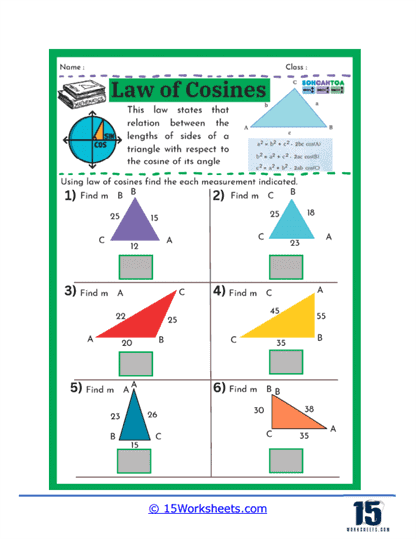
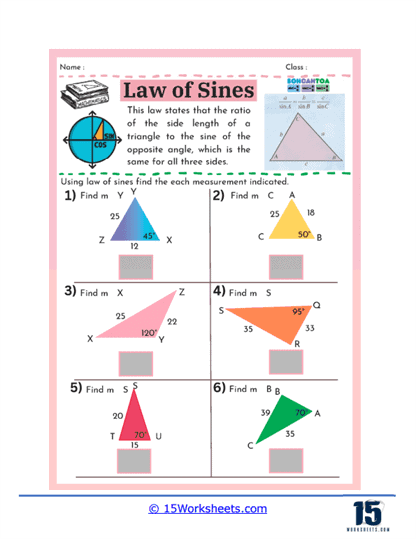
7. Applications of the Law of Sines and Law of Cosines
Worksheets that cover the Law of Sines and the Law of Cosines extend students’ abilities to solve problems involving non-right-angled triangles. These worksheets present scenarios where students must calculate unknown sides and angles using these laws, often in real-world contexts such as navigation, surveying, and physics problems. Exercises may include determining distances, angles of elevation and depression, and solving for components in vector problems.
By engaging with these types of worksheets, students learn how to apply trigonometry beyond right-angled triangles and understand its broader applications. They also develop an appreciation for how trigonometric principles can be used to model and solve practical problems across various fields. This knowledge is particularly beneficial for students pursuing studies in engineering, architecture, and the physical sciences.
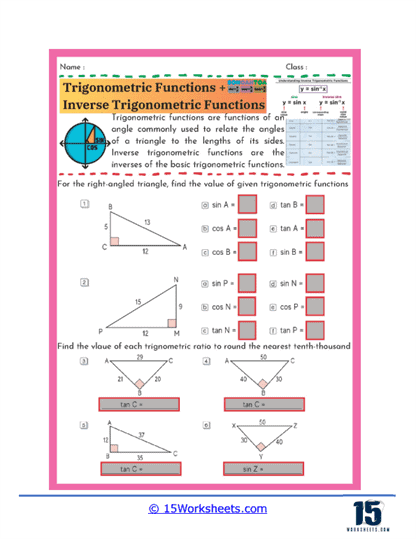
8. Inverse Trigonometric Functions
Worksheets that focus on inverse trigonometric functions help students learn how to determine angle measures when given trigonometric ratios. These exercises typically involve calculating angles using trig functions and may require students to work within specific domains and ranges to find principal and additional solutions.
Practicing with these worksheets enhances students’ understanding of the relationships between angles and ratios and prepares them for solving complex equations and integrals in calculus. They also learn how to interpret and apply inverse functions in various contexts, which is essential for advanced problem-solving and analytical tasks.
9. Trigonometric Form of Complex Numbers
For more advanced students, some worksheets delve into the trigonometric or polar form of complex numbers. These worksheets include exercises where students convert complex numbers between rectangular and polar forms, perform multiplication and division using trigonometric representations, and apply De Moivre’s Theorem to compute powers and roots of complex numbers.
These exercises help students bridge the gap between algebra and trigonometry and understand the profound connections between different areas of mathematics. They develop skills in manipulating and interpreting complex numbers, which are crucial for advanced studies in mathematics, physics, and engineering, particularly in fields like electrical engineering and quantum mechanics.
10. Real-World Applications
These worksheets include a variety of real-world application problems that require students to apply their trigonometric knowledge to practical situations. These word problems might involve calculating heights and distances, modeling periodic phenomena like sound and light waves, analyzing forces and motion, and even solving problems related to architecture and design.
By tackling these problems, students see the relevance and usefulness of trigonometry in everyday life and various professional fields. They learn to translate real-world scenarios into mathematical models, solve for unknowns, and interpret their results in context. This type of practice fosters critical thinking and helps students develop a problem-solving mindset that is valuable beyond the mathematics classroom.
From foundational topics like basic trigonometric ratios and right triangle problems to advanced subjects such as complex numbers and real-world applications, these worksheets offer structured and varied practice opportunities. By consistently working through different types of trigonometry worksheets, students build a robust understanding of mathematical principles, enhance their problem-solving skills, and prepare themselves for further studies in mathematics and related disciplines. The diverse range of exercises ensures that learners can grasp both the theoretical and practical aspects of trigonometry, making them well-equipped to tackle complex challenges both in academics and real-life situations.
What is Trigonometry?
Trigonometry is a branch of mathematics that focuses on the relationships between the sides and angles of triangles, especially right-angled triangles. It has a long history, dating back to ancient civilizations like the Egyptians and Babylonians, who used basic methods to measure angles and distances. However, the study of trigonometry as we know it began with the ancient Greeks. A Greek mathematician named Hipparchus is often called the “father of trigonometry” because he created the first known trigonometric tables around 150 BC. Later, another Greek astronomer named Ptolemy expanded on Hipparchus’s work in his famous book, the “Almagest.”
The main focus of trigonometry is the triangle, particularly the right-angled triangle, which has one angle exactly equal to 90 degrees. In a right-angled triangle, the side opposite the right angle is called the hypotenuse, and it is the longest side of the triangle. The other two sides are called the adjacent and opposite sides, depending on their position relative to the angle you are interested in. Angles in trigonometry are usually measured in degrees (°) or radians (rad). A full circle is 360° or 2π radians, and angles can be acute (less than 90°), right (equal to 90°), or obtuse (greater than 90°).
Trigonometry is based on certain ratios of the lengths of the sides of a right-angled triangle. These ratios are known as the trigonometric ratios, and they are constant for a given angle, no matter how large or small the triangle is. The primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). The sine of an angle is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. There are also three reciprocal trigonometric functions: cosecant (csc), secant (sec), and cotangent (cot), which are the reciprocals of sine, cosine, and tangent, respectively.
In addition to these basic concepts, trigonometry includes a set of identities, which are equations involving trigonometric functions that are true for all values of the angles involved. These identities are useful for simplifying expressions and solving equations. One of the most important trigonometric identities is the Pythagorean identity, which states that sin2(𝜃) + cos2(𝜃) = 1. There are also sum and difference identities, which help calculate the sine or cosine of the sum or difference of two angles, and double angle identities, which deal with the sine or cosine of twice a given angle.
Trigonometry has many practical applications in the real world. For example, it is used in navigation and astronomy to determine the positions of ships, stars, and planets. Engineers use trigonometry to design and analyze structures like buildings, bridges, and skyscrapers. In physics, trigonometry helps describe wave motion and other periodic phenomena, and in computer graphics, it is used to rotate and transform images and render 3D objects on 2D screens. Even in music, trigonometry plays a role in understanding sound waves, which are periodic by nature.
As students progress in their study of trigonometry, they may encounter more advanced topics, such as trigonometric equations, which involve solving for specific angles, and inverse trigonometric functions, which allow us to find the angle when given a trigonometric ratio. Another advanced topic is spherical trigonometry, which deals with triangles drawn on the surface of a sphere, making it especially useful in astronomy and navigation. Trigonometry is also important in fields like signal processing, where it helps break down complex periodic functions into simpler sinusoidal components through Fourier series and transforms.